11.Расчет силы запрессовки колеса на тихоходный вал.

Силу запрессовки определяют из следующей зависимости:

,

где p - давление на валу, вызванное натягом;

d=36 мм - номинальный диаметр;

l= 28 мм - длина соединения;

f=0.1 - коэффициент трения;

Для расчета давления p, используют формулу:

,

где N_р - расчетный натяг;

С₁ - коэффициент жесткости вала;

С₂ - коэффициент жесткости колеса;

Е₁=2×10⁵ Мпа - модуль упругости вала;

Е₂=2×10⁵ Мпа - модуль упругости колеса;

Коэффициенты жесткости вала и втулки определяют по формулам:

,

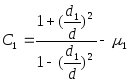где d₁=0 мм - диаметр отверстия в вале (в вале нет отверстия);

m₁=0.3 - коэффициент Пуассона для вала;

и ,

где d₂=144 мм - диаметр колеса;

m₂=0.3 - коэффициент Пуассона для колеса;

Таким образом,

,

и .

Найдём расчетный натяг N_p (посадка H7/s6):

,

где N_max =53 мкм - максимальный натяг по таблице 5.3 [1] ;

U - поправка на смятие, рассчитываемая по формуле:

,

где R_a1=0,8 мкм- среднее арифметическое отклонение профиля вала;

R_a2=0,8 мкм - среднее арифметическое отклонение профиля колеса;

,

Таким образом,

,

и давление p равно:

,

а значит сила запрессовки равна:

.

Определим момент, который может быть передан этим соединением:

,

где S=1,5 - коэффициент запаса.

p_min - минимальное давление в вале для данной посадки вычисляется по формуле:

,

где N_min =24 мкм - минимальный натяг по таблице 5.3 [1].

.

В результате:

.

Получили, что данное соединение не способно передать необходимый момент, поэтому необходима шпонка.

12.Расчет резьбовых соединений.

12.1 Расчёт крепления редуктора к раме.

Исходные данные:

l_тx=140 мм;

l_тy=44 мм;

l_бx=130 мм;

l_бy=44 мм;

a_y=262 мм;

a_x=165 мм;

с=36 мм;

y_max=144 мм;

b=191 мм;

d=12 мм - диаметр болта;

Z=4 - число болтов;

Z_x=2 - число болтов в ряду;

Z_y=2 - число болтов в ряду;

c=0,3 - коэффициент внешней нагрузки;

s_min=2 МПа.

Будем рассчитывать болты класса прочности 3.6. У таких болтов предел текучести равен 180 МПа.

а) Проведем проверку на невозможность сдвига.

Дополнительные исходные данные:

r=154.81 мм;

f=0,1 - коэффициент трения.

1. Приведем силы к центру тяжести:

;

.

2.Найдем наиболее нагруженный винт, полагая, что сила и момент равнораспределены между винтами, т.е.:

и .

Графически определили угол между векторами . Он равенa=60^о;

Þ Равнодействующая сила равна

Þ.

3.Найдем силу затяжки:

.

4. Проверим винт по возникающим в нем напряжениям.

Þ.

Таким образом, невозможность сдвига обеспечена.

б) Проведем проверку на нераскрытие стыка.

1.Приведем внешние силы к центру тяжести стыка:

;

;

.

2. Найдем площадь стыка:

.

3. Определим моменты сопротивления кручению:

;

;

4. Определим напряжения, вызванные внешними силами:

;

;

;

.

Из последнего выражения мы сможем получить силу затяжки.

5. Определим силу затяжки из условия: (считаем ).

Þ

Þ Þ

Þ .

Вывод: сила затяжки, посчитанная из условия отсутствия сдвига, обеспечивает и нераскрытие стыка. обеспечивается автоматически.

Следовательно, выбранные фундаментные болты полностью удовлетворяют требуемым условиям и отвечают требованиям на запас прочности.