Формула Ньютона – Лейбница.

Пусть выполнены условия теоремы о полном дифференциале и пусть выражение

- полный дифференциал, а функция- потенциал.

Тогда справедлива формула Ньютона – Лейбница

, где - потенциал.

Доказательство.В теореме о полном дифференциале доказано, что потенциал можно записать в виде . Так как интеграл не зависит от пути интегрирования, то дугу, соединяющую точки (x₁,y₁), (x₂,y₂) можно провести через точку (x₀,y₀). Поэтому = + = - = .

Теорема (о полном дифференциале) для пространственной кривой.

Пусть дуга ABлежит на кусочно-гладкой поверхностиS, пусть функцииP(x,y,z),Q(x,y,z),R(x,y,z) непрерывны и имеют непрерывные частные производные наS. Тогда следующие четыре утверждения эквивалентны.

1. не зависит от формы дуги (от пути интегрирования), а зависит только от начальной и конечной точек дуги.

2. Для любого замкнутого контура

3. 

4. . - полный дифференциал.

Доказательство. Доказательство аналогично двумерному случаю, схема доказательства та же: . Докажите ее самостоятельно.

проводится по теореме о смешанных производных так же как в двумерном случае.

проводится по теореме Стокса (будет сформулирована и доказана ниже).

доказательство полностью аналогично двумерному случаю.

доказательство аналогично двумерному случаю.

Замечание. Формула Ньютона-Лейбница справедлива в трехмерном случае и доказывается так же.

Вычисление криволинейного интеграла от полного дифференциала.

Криволинейный интеграл от полного дифференциала можно вычислять двумя способами.

1. Можно выбирать удобный путь интегрирования, например, состоящий из отрезков, параллельных OXиOY. На отрезке, параллельномOX,dy=0, так какyне изменяется на этом отрезке. На отрезке, параллельномOY,dx=0, так какxне изменяется на этом отрезке. Тогда = +

2. Можно восстановить потенциал, как это делалось на первом курсе при решении дифференциальных уравнений в полных дифференциалах и применить формулу Ньютона-Лейбница.

Пример.Вычислить интеграл .

1. =

2. 

.

Сравнивая две записи потенциала, получим .

=.

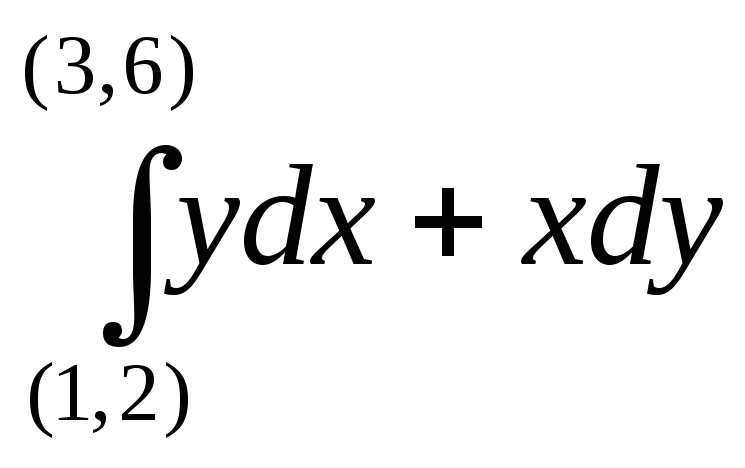Заметим, что аналогично вычисляется криволинейный интеграл от полного дифференциала по пространственной кривой.

Формула Грина для многосвязной области.

Пусть кусочно-гладкие контуры лежат внутри контура и вне друг друга. Пусть непрерывны и имеют непрерывные частные производные по переменнымx,yв области между контурами и на самих этих контурах. Тогда

D m A K B E p q r s n

Соединим контуры линиями AB,CD,EK. По формуле Грина для односвязной области криволинейные интегралы по контуру AbpCDqEKmAи по контуруAnKEsDCrBAравны двойным интегралам для верхнейDверх и нижнейDнижнобластей. Представим эти интегралы как сумму интегралов по составляющим контуры дугам и сложим эти интегралы, сокращая интегралы по одним и тем же дугам в разных направлениях

=

=

Складывая интегралы, получим

=.

Отсюда имеем

= . Теорема доказана для случаяn= 2. Дляn> 2 доказательство аналогично.

Следствие 1. ПустьPdx+Qdy– полный дифференциал иn=1.

Тогда. Поэтому, если в какой-либо точке нарушается непрерывность функций,P,Qили их частных производных, то интеграл может быть взят по любому кусочно-гладкому не самопересекающемуся контуру, охватывающему эту точку (мы получим один и тот же результат).

Следствие 2. ПустьPdx+Qdy– полный дифференциал Если кусочно-гладкий контур один раз охватывает некоторую точку, , а контурLn раз охватывает эту точку, то в условиях теоремы . Докажите это самостоятельно.