Вычисление тройного интеграла в декартовой системе координат.

(x,y) (x,y)

Пусть пространственное тело проектируется на плоскость OXYв областьD, а на осьOZв отрезок [c,d].Пусть «верхняя» граница тела описывается уравнением поверхностиz=(x,y), «нижняя» – уравнением z =(x,y). Пусть элемент Vпространственного телаVпроектируется на плоскостьOXYв областьDxy, а на осьOZв отрезок [z,z+z]. Для того чтобы вычислять тройной интеграл как предел интегральных сумм, нужно в интегральной сумме перебирать эти элементы по определенному алгоритму.

Если сначала перебирать элементы в столбце над областью D_xy, от нижней границы до верхней (внутренний интеграл), а затем перемещать областьD_xyвD(внешний двойной интеграл), то получим повторный интеграл.

Если сначала перебирать элементы в слое [z,z+z] (внутренний интеграл), а затем .перемещать слой на [c,d], (внешний интеграл), то получим повторный интеграл.И в том, и в другом случае тройной интеграл сводится к определенному и двойному интегралам.

Пример. Вычислить массу тетраэдра плотностьюf(x,y,z) =z, ограниченного плоскостямиx+y+z= 1,x+z=1,x+y= 1,y+z=1.

1

Лекция 4. Приложения тройного интеграла.

Замена переменных в тройном интеграле.

Теорема.Пусть с помощью непрерывных функцийx=x(u,v,w),y=y(u,v,w), z =z(u,v,w) имеющих непрерывные частные производные установлено взаимно однозначное соответствие пространственно односвязных ограниченных, замкнутых областейD_xyz,D_uvwс кусочно-гладкой границей. Тогда

, где-якобиан(определитель Якоби).

Теорема приведена без доказательства.

Цилиндрическая система координат.

M

Вводятся цилиндрические координаты ,,h. x=cos,y=sin, z = h. Вычислим якобиан

ПримерВычислить объем пространственного тела, заключенного между цилиндрической поверхностьюи эллиптическим параболоидом..

Сферическая система координат.

 x y z r  

Сферические координаты ,r,. x= rsincos y= r sin sin z = r cos. Вычислим якобиан

Пример.Найти массу части шара (с центром в начале координат, радиусомR), находящейся в первом октанте, если плотность вещества шарав каждой точке шара пропорциональна расстоянию этой точки от осиOZ.

Приложения тройного интеграла.

Геометрическое приложение –вычисление объемалюбого пространственного тела.

По свойству 3 тройного интеграла , где– объем областиV.

С помощью двойного интеграла тоже можно вычислять объем, но только цилиндрического тела, а не произвольного.

Пример.Вычислить объем пространственного тела, ограниченного эллиптическим параболоидоми шаром ( единичного радиуса с центром в точке (0, 0, 1))

.

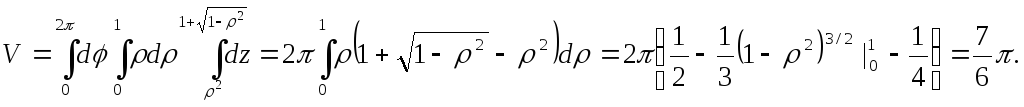
Механические приложения–вычисление массы пространственного тела, статических моментов, центра тяжести, моментов инерции по формулам, которые выводятся аналогично соответствующим формулам для плоского тела с двойным интегралом (- плотность вещества тела в каждой точке).

,,. Формулы для моментов инерции запишите сами (например,)

Пример.Определить координаты центра тяжести полушара,По симметрии.,