Приложения двойного интеграла.

С помощью двойного интеграла можно вычислить объем цилиндрического тела, площадь и массу плоской области. От этих задач мы и пришли к двойному интегралу.

Но возможны и менее очевидные приложения.

С помощью двойного интеграла можно вычислять площадь поверхности, определять статические моменты, моменты инерции и центр тяжести плоской области.

Вычисление площади поверхности с помощью двойного интеграла.

Пусть поверхность , площадь которой надо вычислить, задана уравнениемF(x,y,z) = 0 или уравнениемz=f(x,y). Введем разбиение на ячейкиk, не имеющие общих внутренних точек, площадьюvk. Пусть областьи ячейкиk проектируются на плоскостьOXYв областьDи ячейкиdkплощадьюsk. Отметим на ячейкеdkточкуMk.В точкеQk(ячейкиk), которая проектируется в точкуMk, проведем единичный вектор нормалиnk{cosk,cosk,cosk} к поверхностии касательную плоскость. Если приближенно считать равными площадьvkячейкиkи площадь ее проекции на касательную плоскость,

то можно считать справедливым соотношение v_kcos_k=s_k. Выразим отсюда

v_k=s_k/cos_k. Будем измельчать разбиение при условииmaxdiam_k0, что для кусочно-гладкой поверхности, не ортогональной плоскостиOXY, равносильноmaxdiamd_k0. Вычислим площадь поверхности как двойной интеграл

.

Сюда остается лишь подставить .

Если поверхность задана уравнениемF(x,y,z) = 0, то

Поэтому в этом случае ,.

.

Если поверхность задана уравнением z=f(x,y), то уравнение это можно

свести к уравнению F(x,y,z) = 0 и применить выведенную формулу:

.

Пример.Вычислить площадь поверхности конуса, ограниченной плоскостями

. .

Вычисление статических моментов, координат центра тяжести, моментов инерции.

Пусть задана плотность вещества плоской материальной области D(x,y). Выделим элементарную ячейку с массойdmи применим к ней известные формулы для материальной точки:

Статические моменты относительно осей OX,OYdm_x =ydm=y(x,y) ds,

dm_y = x dm = x (x, y) ds.

Моменты инерции относительно осей OX,OYdJ_x=y²dm=y²(x,y) ds,

dJ_y = x² dm = x² (x, y) ds.

Момент инерции относительно начала координат dJ₀=dJ_x+dJ_y.

Двойным интегралом по всей области Dвычисляем те же характеристики для областиD.

, , , ,J₀=J_x +J_y.

Координаты центра тяжести , где - масса областиD.

Пример.Вычислить координаты центра тяжести полукругас заданной плотностью.

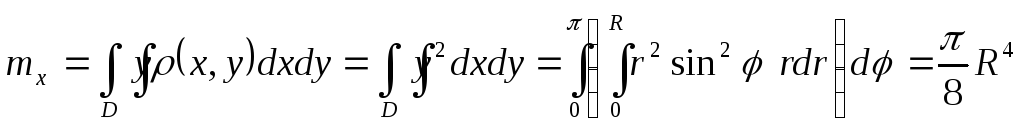
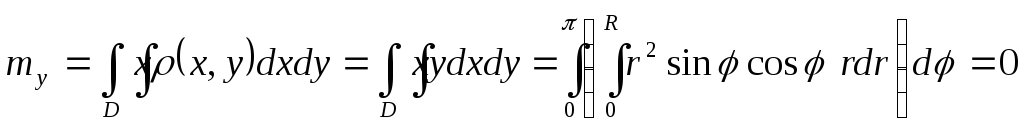(это было ясно заранее, по симметрии полукруга относительноOYи независимости плотности от координатыx).

Поэтому .

Пример.Вычислить момент инерции полукруга с заданной плотностью относительно прямой .

.

Эта формула известна в теоретической механике.

Замечание о несобственных двойных интегралах.

Точно так же, как и в определенных интегралах, вводят несобственные двойные интегралы двух типов: интеграл от непрерывной функции по неограниченной области (первого рода) иинтеграл от разрывной функции по ограниченной области (второго рода).

Интеграл первого рода определяют как предел последовательности двойных интегралов от непрерывной функции по «расширяющимся» областям, стремящимся к заданной неограниченной области. Если предел существует и конечен, то интеграл называется сходящимся, если предел не существует или бесконечен, то интеграл называется расходящимся.

Интеграл второго рода⁶определяют как предел последовательности интегралов от непрерывной функции по «расширяющимся» областям, стремящимся к заданной области и исключающим точку разрыва. Если предел существует и конечен, то интеграл называется сходящимся, если предел не существует или бесконечен, то интеграл называется расходящимся.

Пример.Показать, что несобственный интеграл первого рода по области сходится при и расходится при .

Показать, что несобственный интеграл первого рода по области сходится при и расходится при .Вычислим этот интеграл по области .

.

=

=

Часто расширение математических знаний позволяет решать задачи, которые не получались старыми методами.

Пример.Вычислить интеграл Пуассона .

Неопределенный интеграл «не берется». Но двойной интеграл по области равен

I=.

С другой стороны, переходя к полярным координатам, получим

I = .

Поэтому = . По четности .