
- •Галкин с.В.
- •Двойной интеграл1
- •Вычисление двойного интеграла в декартовой системе координат.
- •Геометрический и физический «смысл» двойного интеграла.
- •Лекция 2. Приложения двойного интеграла.
- •Приложения двойного интеграла.
- •Вычисление площади поверхности с помощью двойного интеграла.
- •Вычисление статических моментов, координат центра тяжести, моментов инерции.
- •Замечание о несобственных двойных интегралах.
- •Лекция 3 Тройной интеграл. Задача о массе пространственного тела.
- •Свойства тройного интеграла.
- •Вычисление тройного интеграла в декартовой системе координат.
- •Лекция 4. Приложения тройного интеграла.
- •Лекция 5 Криволинейные интегралы 1 и 2 рода, их свойства.. Задача о массе кривой. Криволинейный интеграл 1 рода.
- •Вычисление криволинейного интеграла первого рода.
- •Криволинейный интеграл 2 рода. Задача о работе силы.
- •Теорема существования.
- •Свойства криволинейного интеграла 2 рода.
- •Вычисление криволинейного интеграла второго рода.
- •Лекция 6. Формула Грина.
- •Вычисление площади области по формуле Грина.
- •Полный дифференциал и его вычисление.
- •Формула Ньютона – Лейбница.
- •Вычисление криволинейного интеграла от полного дифференциала.
- •Формула Грина для многосвязной области.
- •Лекция 7. Поверхностные интегралы.
- •Свойства поверхностного интеграла первого рода.
- •Вычисление поверхностного интеграла первого рода.
- •Поверхностный интеграл второго рода.
- •Задача о потоке жидкости через поверхность.
- •Запись поверхностного интеграла второго рода.
- •Лекция 8 Скалярное и векторное поля.
- •Скалярные поля.
- •Векторное поле.
- •Формула Остроградского – Гаусса.
- •Инвариантное определение дивергенции.
- •Свойства дивергенции.
- •Соленоидальное поле и его свойства.
- •Свойства соленоидального поля.
- •Лекция 9 Формула Стокса. Ротор векторного поля.
- •Свойства ротора.
- •Теорема Стокса.
- •Инвариантное определение ротора.
- •Потенциальное поле и его свойства.
- •Свойства потенциального поля.
- •Оператор Гамильтона
- •Дифференциальные операции второго порядка.
- •Гармоническое поле.
- •Часть 2. Числовые и функциональные ряды Лекция 10. Числовые ряды и их свойства.
- •Свойства сходящихся рядов.
- •Лекция 11 Знакоположительные ряды.
- •Интегральный признак Коши.
- •Признаки сравнения рядов.
- •Признак Даламбера.
- •Лекция 12. Знакопеременные ряды.
- •Теорема Римана.
- •Знакочередующиеся ряды.
- •Признак Лейбница.
- •Функциональные ряды Лекция 13. Равномерно сходящиеся ряды.
- •Свойства равномерно сходящихся функциональных рядов.
- •Лекция 14. Степенные ряды.
- •Определение радиуса и интервала сходимости степенного ряда.
- •Лекция 15. Ряд Тейлора.
- •Разложение в ряд Маклорена основных элементарных функций.
- •Применение степенных рядов.
- •Содержание
- •Часть1 Кратные, криволинейные интегралы, теория поля
- •Часть 2 Числовые и функциональные ряды.
Вычисление двойного интеграла в декартовой системе координат.
Предположим, что D– плоская область, лежащая в некоторой плоскости и введем в этой плоскости декартову систему координат.
Область Dназовемправильной, если любая прямая, параллельная декартовым осям, пересекает ее не более чем в двух точках.
Можно показать, что замкнутую ограниченную область с кусочно-гладкой границей можно представить в виде объединения правильных областей, не имеющих общих внутренних точек. Поэтому интеграл по области Dможно вычислять как сумму интегралов (свойство 2) по правильным областям. Будем считать, что нам надо вычислить двойной интеграл по правильной области.
|
|
Вспомним формулу для вычисления объема тела по площадям параллельных сечений
|
Подставляя
![]() в
формулу для объема, получим
в
формулу для объема, получим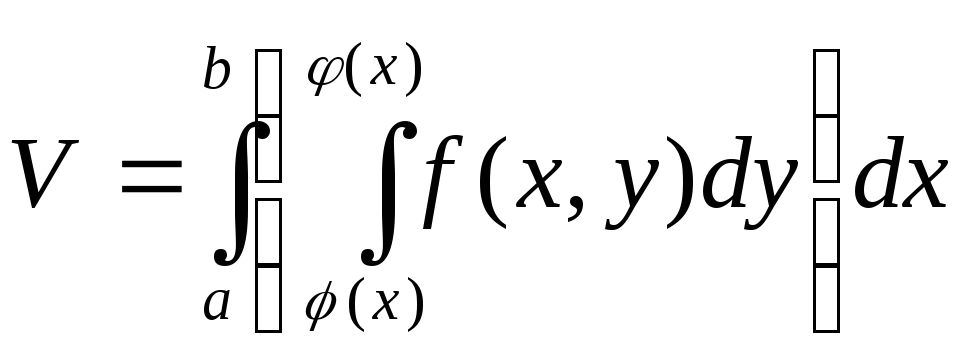 .
Это повторный интеграл, вернее один из
них. Второй повторный интеграл можно
получить, вводя сечения, параллельные
осиOX. По аналогии
.
Это повторный интеграл, вернее один из
них. Второй повторный интеграл можно
получить, вводя сечения, параллельные
осиOX. По аналогии
 .
По смыслу двойного интеграла (объем
цилиндрического тела)
.
По смыслу двойного интеграла (объем
цилиндрического тела)
 =
=![]() =
=
![]()
Примеры. Записать двойной интеграл по заданной области и повторные интегралы.
1.
|
1 |
|
|
|
|
|
|
|
|
Геометрический и физический «смысл» двойного интеграла.
К двойному
интегралу
![]() .мы
пришли от задачи об объеме цилиндрического
тела, расположенного над областьюDс переменной высотой
.мы
пришли от задачи об объеме цилиндрического
тела, расположенного над областьюDс переменной высотой![]() .
.
В этом и состоит его геометрический смысл.
Можно рассмотреть
задачу о массе плоской пластины,
представляющей собой плоскую область
D, плотность которой равна![]() ,
т.е. меняется от точки к точке. Достаточно
ассоциировать переменную плотность с
переменной высотой в задаче об объеме,
чтобы понять, что мы имеем ту же модель.
,
т.е. меняется от точки к точке. Достаточно
ассоциировать переменную плотность с
переменной высотой в задаче об объеме,
чтобы понять, что мы имеем ту же модель.
Поэтому физический
смысл двойного интеграла заключается
в том, что
![]() равен массе плоской областиD,
плотность которой равна
равен массе плоской областиD,
плотность которой равна![]() .
.
Пример. Вычислить объем Vцилиндрического тела, ограниченного двумя параболическими цилиндрамиz= 1-y2 иx=y2и площадь его основанияD, расположенного в плоскостиOXY..
|
|
|
Лекция 2. Приложения двойного интеграла.
Теорема. Пусть
установлено взаимно однозначное
соответствие областейDxyиDuvс помощью непрерывных, имеющих непрерывные
частные производные функций![]() .
Пусть функцияf(x,y)
непрерывна в областиDxy.
Тогда
.
Пусть функцияf(x,y)
непрерывна в областиDxy.
Тогда
![]() ,
где
,
где
 - якобиан (определитель Якоби).
- якобиан (определитель Якоби).
Доказательство
(нестрогое). Рассмотрим элементарную
ячейку в координатах u,v:Q1,Q3,Q4,Q2– прямоугольник
со сторонамиdu,dv.
Рассмотрим ее образ при отображении![]() - ячейкуP1,P3,P4,P2.
- ячейкуP1,P3,P4,P2.
|
u v Q3 Q1 Q2 Q4 P1 P2 P4 P3 x y |
Запишем координаты точек Q1(u,v),Q2(u+du,v),Q3(u,v+dv),
|
Приближенно
будем считать ячейку P3,P4,P1,P2.параллелограммом,
образованным сторонами![]() .
Вычислим площадь этой ячейки как площадь
параллелограмма.
.
Вычислим площадь этой ячейки как площадь
параллелограмма.
 .
.
Подставляя в
интеграл площадь параллелограмма в
качестве площади ячейки dxdy,
получим![]() .
.
Следствие.
Рассмотрим частный случай – полярную
систему координат![]() :
:![]() .
. .
.
Пример.Вычислить площадь внутри кардиоиды![]() .
.
 .
.
Пример.Вычислить объем внутри прямого кругового
цилиндра![]() ,
ограниченный плоскостью
,
ограниченный плоскостью![]() в первом октанте.
в первом октанте.
![]() .
.
Для каждой задачи можно выбрать ту систему координат, в которой вычисления проще. Декартова система координат удобна для прямоугольных областей. Если стороны прямоугольника параллельны координатным осям, то пределы интегрирования в повторном интеграле постоянны. Полярная система координат удобна для круга, кругового сектора или сегмента. Если центр круга находится в начале координат, то пределы интегрирования по углу и радиусу постоянны.







 -
площадь криволинейной трапеции..
-
площадь криволинейной трапеции..



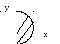 1.
1.


 =
=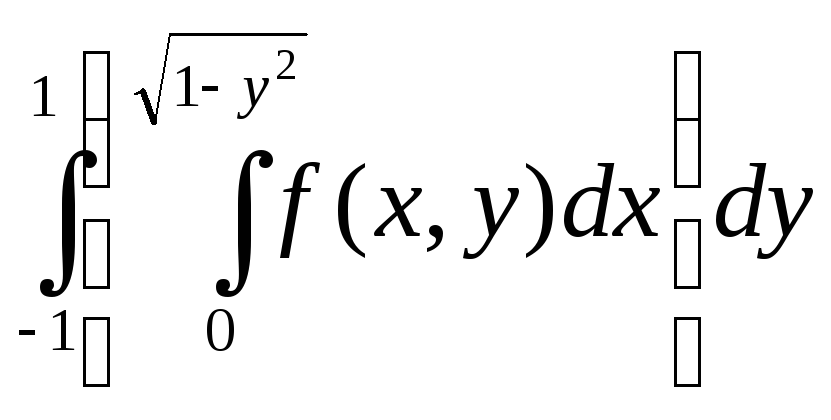 =
=


 2.
2.
 +
+ =
= +
+
 3.
3.
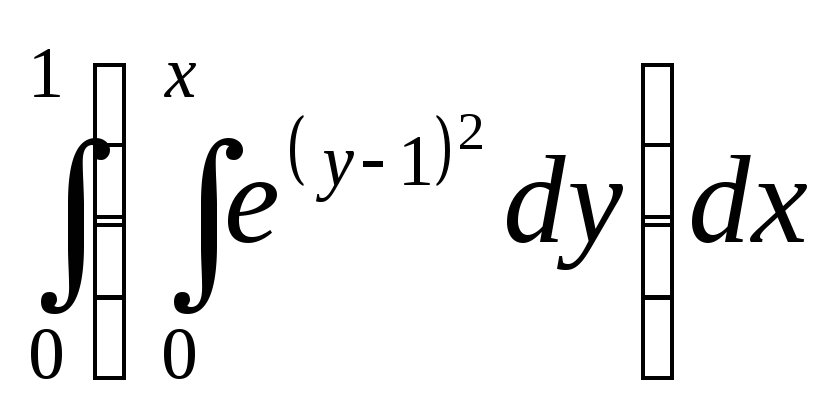 (
внутренний интеграл не берется)=
(
внутренний интеграл не берется)= =
=
















