Инвариантное определение ротора.

Рассмотрим произвольную точку Mв областиV. Проведем через нее поверхность, границей которой служит контур. Пусть поверхность и контур удовлетворяют условиям теоремы Стокса. По теореме о среднем для поверхностного интеграла и формуле Стокса получим

.

Здесь, как и ранее - обозначение области и ее площади. Из этого соотношения, стягивая контурк точкеM, получим

Это и есть инвариантное определение ротора.

Правая часть формулы – это поверхностная плотность циркуляции векторного поля (энергии в точке Mвращения векторного поля или работы векторного поля при вращении вокруг некоторого направления, определяемого вектором). Левая часть – это проекция ротора на это направление.

Если направление совпадает с направлением ротора и- единичный вектор, то левая часть равна модулю ротора. Поэтомумодуль ротора векторного поля равен максимальному значению поверхностной плотности циркуляции векторного поля.

Левая часть достигает максимума при коллинеарности направления и ротора векторного поля. Поэтому направление ротора векторного поля – это то направление, вокруг которого поверхностная плотность циркуляции векторного поля – наибольшая.

Пример.Найти ротор линейной скорости вращения с постоянной угловой скоростью

Векторное поле линейной скорости .

,

Ранее была сформулирована теорема о полном дифференциале для пространственной кривой. В ее доказательстве не хватало только одного пункта – перехода от пункта 3) к пункту 2). Все остальное доказывается аналогично случаю плоской кривой.

Теорема (о полном дифференциале) для пространственной кривой.

Пусть дуга ABлежит на кусочно-гладкой поверхностиS, пусть функцииP(x,y,z),Q(x,y,z),R(x,y,z) непрерывны и имеют непрерывные частные производные наS. Тогда следующие четыре утверждения эквивалентны.

1. не зависит от формы дуги (от пути интегрирования), а зависит только от начальной и конечной точек дуги.

2. Для любого замкнутого контура

3. 

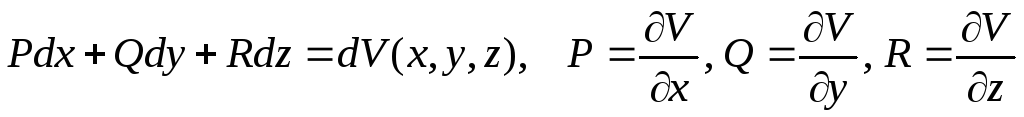4. . - полный дифференциал.

Теперь переход от пункта 3) к пункту 2) легко сделать по формуле Стокса.

Криволинейный интеграл от полного дифференциала можно вычислять по формуле

=, так как интеграл не зависит от формы дуги (пути интегрирования).

Криволинейный интеграл от полного дифференциала можно вычислять также по формуле Ньютона – Лейбница

=, где- потенциал векторного поля ().

Потенциальное поле и его свойства.

Векторное поле называетсяпотенциальным, если существует такое скалярное поле (потенциалвекторного поля), что=.

Замечание. Если поле- потенциально, то=- полный дифференциал. Тогда- полный дифференциал. Поэтому свойства потенциального поля можно сформулировать и доказать как следствия теоремы о полном дифференциале.

Свойства потенциального поля.

1. Линейный интеграл потенциального поля не зависит от формы дугиL= , а зависит только от начальной и конечной точек дуги.

В самом деле, =.

2. Циркуляция потенциального поля равна нулю

Полагая дугу АВ замкнутой (A=B), получаем =

3. Потенциальное поле является безвихревым, т.е.

Оператор Гамильтона

Оператор Гамильтона .

Применим оператор Гамильтона к скалярному полю .

Оператор Гамильтона представляет собой вектор-оператор. Его можно скалярно или векторно умножить на векторное поле .

Это дифференциальные операции первого порядка над скалярным и векторным полями. От скалярного поля можно взять градиент, от векторного поля можно взять дивергенцию и ротор.