6.4.3.4. Механические и физические приложения поверхностного интеграла 1-го рода.

6.4.3.4.1. Масса поверхности. Пусть на поверхности  распределена масса с поверхностной плотностью (x,y,z). Тогда масса m поверхности равна

m = .

6.4.3.4.2. Статические моменты и центр масс. Статические моменты поверхности относительно координатных плоскостей OYZ, OXZ, OXY равны соответственно

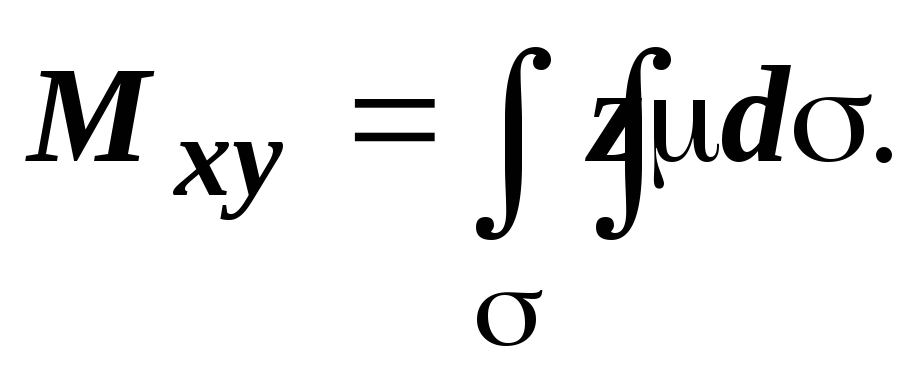
Координаты центра масс поверхности  равны x_c = ,y_c = ,z_c = .

6.4.3.4. 3. Моменты инерции. Момент инерции поверхности  относительно прямой L равен I_L=, где=r_L(x,y,z) - расстояние от точки (x,y,z), лежащей на поверхности , до прямой L. В частности, моменты инерции относительно координатных осей OX, OY, OZ равны

, ,.

Момент инерции относительно точки P(x₀,y₀,z₀) равен

Момент инерции относительно начала координат равен

Пример. Найти координаты центра масс полусферы x² + y² + z² = R², z  0, если поверхностная плотность в каждой точке сферы равна расстоянию от этой точки до оси OZ.

Решение: Масса полусферы  равна

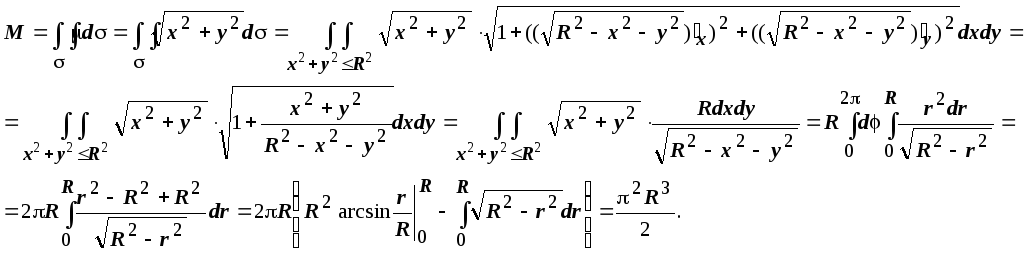
(Мы воспользовались тем, что интеграл равен четверти площади круга радиусаR т.е. ).

44