ОП_ЛР11
.docx
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ
-
Федеральное государственное автономное образовательное учреждение высшего образования
«Санкт-Петербургский государственный университет аэрокосмического приборостроения»
КАФЕДРА № 2
Преподаватель
Ст. преподаватель Куртяник Д.В.
Отчёт
по лабораторной работе №11
по дисциплине Информатика
на тему: « Передача имён функций в качестве параметров»
Работу выполнил
студент гр. 4616 Павлов А.В.
Санкт-Петербург
Цель лабораторной работы: изучение методов передачи имён функций в качестве параметров других функций; изучение методов нахождения значения определённых интегралов функций на заданном отрезке и с заданной точностью; совершенствование навыков процедурного программирования на языке C/С++ при решении задач с использованием рекурсивных функций.
Задание на программирование: используя технологию процедурного программирования реализовать заданный метод нахождения значения определённого интеграла произвольных функций на заданном отрезке и с заданной точностью и применить его для определения площадей областей на плоскости в соответствии с индивидуальным заданием.
Порядок выполнения работы:
1) Получить у преподавателя индивидуальное задание:
- метод нахождения значения определённого интеграла произвольной функции на заданном интервале интегрирования и с заданной точностью;
- задачу определения места нахождения точки с произвольно заданными координатами на координатной плоскости (вариант и формулировка этой задачи берётся из лабораторной работы №2).
2) Разработать математическую модель:
- привести уравнения линий, ограничивающих выделенные штриховкой области;
- описать условия попадания точки в каждую выделенную область;
- составить аналитические формулы определения площади каждой выделенной области;
- определить аналитический вид функций, графики которых совпадают с видом линий, ограничивающих выделенные штриховкой области;
- определить площадь каждой выделенной области с использованием значений определённых интегралов соответствующих функций на заданном интервале интегрирования и с заданной точностью.
3) Построить схему алгоритма решения задачи.
4) Составить программу на языке C/С++.
5) Входные данные должны вводиться с клавиатуры по запросу.
Выходные данные (сообщения) должны выводиться на экран в развернутой форме.
6) Использовать стандартные потоковые объекты ввода/вывода cin и cout.
7) Проверить и продемонстрировать преподавателю работу программы на полном наборе тестов.
8) Оформить отчет о лабораторной работе в составе: постановка задачи, математическая модель, схема алгоритма решения, текст программы, контрольные примеры.
1-3)
Вариант 9
Метод криволинейных трапеций.
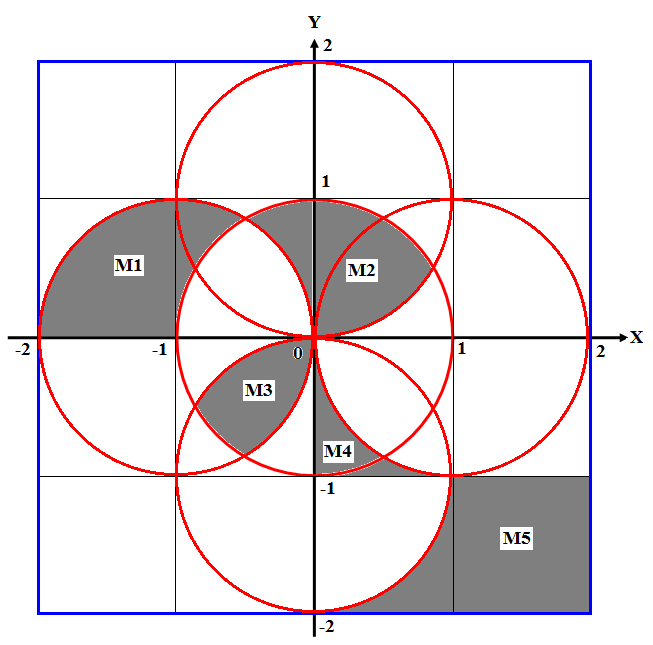
Математическая модель (условия принадлежности точек выделенным областям)
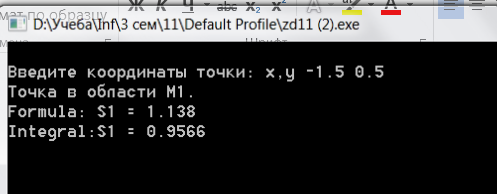
- условие 1 (принадлежность области М1):
(x + 1)2 + y2 < 1 {внутри левой окружности}
x 2 + y2 > 1 {за окружности}
y > 0 {выше линии y = 0}
Площадь области М1:
S=x/2-(0.5-√2)/ √2=1.338
Аналитический вид функций, подлежащих интегрированию:
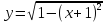
интервал интегрирования [-2, -0.5]
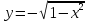
интервал интегрирования [-1, -0.5]
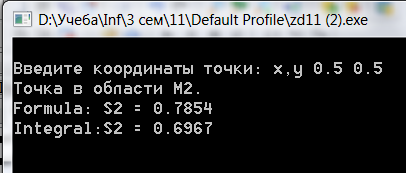
- условие 2 (принадлежность области М2):
x 2 + y2 < 1 {в центральной окружности}
(x + 1)2 + y2 > 1 { вне левой окружности
x2
+ (y-1)
2 > 1 {вне
верхней окружности }
Площадь области М2:
площадь четверти круга (πr2 / 4) = π / 4 ≈0.785
Аналитический вид функций, подлежащих интегрированию:

интервал
интегрирования [ -0.5,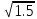 ]
]
y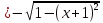
интервал интегрирования [ -0.5,0]
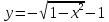
интервал интегрирования [0, 1]
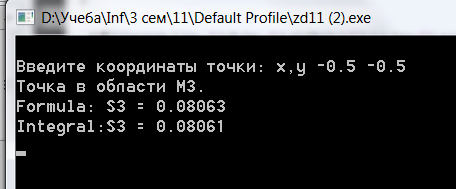
- условие 3 (принадлежность области М3):
(x + 1)2 + y2 < 1 { внутри левой окружности }
x2 + y2 < 1 {в центральной окружности}
x2 + (y+1) 2 < 1 {внутри верхней окружности }
Площадь области М3:
√3/2-(πr2 / 4)=0.806
Аналитически Аналитический вид функций, подлежащих интегрированию:
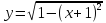
интервал
интегрирования [ -0.5,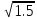 ]
]
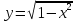
интервал
интегрирования [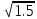 ,-0.5]
,-0.5]
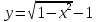
интервал интегрирования [-0.5, 0]
- условие 4 (принадлежность области М4):
(x - 1)2 + y2 > 1 {вне правой окружности}
y < 0 {ниже оси x}
y> -1 {выше линии y = -1}
x> 0 {правее линии x = 0}
x< 1 {левее x=1}
Площадь области М4:
(1 – πr2 / 4) ≈0.42
Аналитический вид функций, подлежащих интегрированию:

интервал интегрирования [0,1]

интервал интегрирования [0, 1]
- условие 5 (принадлежность области М5):
x2 + (y+1) 2 > 1 {вне левой окружности}
y > -2 {выше линии y = -2}
y <-1 {ниже линии y = -1}
x > 0 {правее линии x = 0}
x < 2 {левее x=2}
Площадь области М5:
(1 – πr2 / 4) ≈1.42
Аналитический вид функций, подлежащих интегрированию:
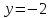
интервал интегрирования [0,1]

интервал интегрирования [0, 1]
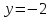
интервал интегрирования [1,2]
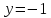
интервал интегрирования [1,2]
Текст программы
#include <iostream>
#include <math.h>
#include <locale.h>
using namespace std ;
typedef double(*Tfun)(double) ;
double integral(double, double, double, double, Tfun, double) ;
double fun1(double x) ;
double fun2(double x) ;
double fun3(double x) ;
double fun4(double x) ;
double fun5(double x) ;
double fun6(double x) ;
double fun7(double x) ;
double fun8(double x) ;
double fun9(double x) ;
double fun10(double x) ;
int main()
{int i = 0 ; //номер области
float x, y, //координаты точки
s1, s2, s3, s4, s5 ; //площади областей
float eps = .00001, //точность вычисления
shag= .001, //начальный шаг вычисления
s ; //значение определённого интеграла
setlocale(LC_ALL,"Russian") ;
cout << '\n' << "Введите координаты точки: x,y " ;
cin >> x >> y ;
cout.precision(4) ; //число знаков после дес. точки
if((sqrt((x+1)*(x+1)+y*y)<1)&&(sqrt(x*x+y*y)>1)&&(y>0))
{i=1;
cout << "Точка в области М1. " << endl ;
cout << "Formula: S1 = " << (s1 = M_PI/2-sqrt(3)/4) << endl ;
cout << "Integral:S1 = " << (s1 = integral(-2, -0.5, shag, eps, fun1, s)- integral(-1, -0.5, shag, eps, fun2, s))<<endl ;
}
if((sqrt(x*x+y*y)<1)&&(sqrt(x*x+(y-1)*(y-1))<1)&&(sqrt((x+1)*(x+1)+y*y)>1))
{i=1;
cout << "Точка в области М2. " << endl ;
cout << "Formula: S2 = " << (s2 = M_PI/4) << endl ;
cout << "Integral:S2 = " << (s2 = integral(-0.5, (sqrt(3)/2), shag, eps, fun2, s)- integral(-0.5, 0, shag, eps, fun1, s)- fabs(integral(0, 1, shag, eps, fun3, s)))<<endl ;
}
if((sqrt(x*x+y*y)<1)&&(sqrt((x+1)*(x+1)+y*y)<1)&&(sqrt(x*x+(y+1)*(y+1))<1))
{i=1;
cout << "Точка в области М3. " << endl ;
cout << "Formula: S3 = " << (s3 = sqrt(3)/2-M_PI/4) << endl ;
cout << "Integral:S3 = " << (s3 = -integral((-sqrt(3)/2), 0, shag, eps, fun4, s)-integral((-sqrt(3)/2), -0.5, shag, eps, fun5, s)+integral(-0.5, 0, shag, eps, fun6, s))<<endl ;
}
if((sqrt((x-1)*(x-1)+y*y)>1)&&(x>0)&&(x<1)&&(y<0)&&(y>-1))
{i=1;
cout << "Точка в области М4. " << endl ;
cout << "Formula: S4 = " << (s4 =1-M_PI/4) << endl ;
cout << "Integral:S4 = " << (s4 = fabs(integral(0, 1, shag, eps, fun7, s))- fabs(integral(0, 1, shag, eps, fun8, s)))<<endl ;
}
if((sqrt(x*x+(y+1)*(y+1))>1)&&(x>0)&&(x<2)&&(y<-1)&&(y>-2))
{i=1;
cout << "Точка в области М5. " << endl ;
cout << "Formula: S5 = " << (s5 = 2-M_PI/4) << endl ;
cout << "Integral:S5 = " << (s5 = fabs(integral(0, 1, shag, eps, fun9, s))- fabs(integral(0, 1, shag, eps, fun10, s))+fabs(integral(1,2, shag, eps, fun9, s))-fabs(integral(1, 2, shag, eps, fun7, s)))<<endl ;
}
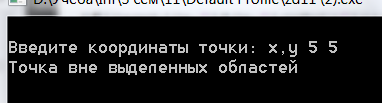
if(i!=1) cout<<"Точка вне выделенных областей"<<endl;
return 0 ;
}
//нахождение определенного интеграла методом трапеции
double integral(double a, double b, double h, double eps, Tfun fun, double s1)
{double x, s = 0 ;
int n, i ;
n = (b - a) / h ;
for (i = 0; i < n; i++)
{x = a + i * h + h / 2 ;
s += fun(x) ;
}
s *= h ;
if (fabs(s - s1) > eps)
s = integral(a, b, h / 2, eps, fun, s) ;
return s ;
}
//описание вида функции №1: (x+1)^2+y^2=1 (верхняя полуокружность)
double fun1(double x)
{return(sqrt(-2*x - x * x)) ;}
//описание вида функции №2: x^2+y^2=1 (верхняя полуокружность)
double fun2(double x)
{return(sqrt(1-x*x)) ;}
//описание вида функции №3: x^2+(y-1)^2=1 (нижняя полуокружность)
double fun3(double x)
{return(-sqrt(1-x*x)+1) ;}
//описание вида функции №4: x^2+(y+1)^2=1 (верхняя полуокружность)
double fun4(double x)
{return(sqrt(1-x*x)-1) ;}
//описание вида функции №5: x^2+y^2=1 (нижняя полуокружность)
double fun5(double x)
{return(-sqrt(1-x*x)) ;}
//описание вида функции №6: (x+1)^2+y^2=1 (нижняя полуокружность)
double fun6(double x)
{return(-sqrt(-2*x-x*x)) ;}
//описание вида функции №7: y=-1
double fun7(double x)
{return -1 ;}
//описание вида функции №8: (x-1)^2+y^2=1 (нижняя полуокружность)
double fun8(double x)
{return(-sqrt(2*x-x*x)) ;}
//описание вида функции №9: y=-2
double fun9(double x)
{return -2 ;}
//описание вида функции №10: x^2+(y+1)^2=1 (нижняя полуокружность)
double fun10(double x)
{return(-sqrt(1-x*x)-1) ;}
Примеры.