
- •С.В. Галкин
- •Задача о наилучшем приближении в н (гильбертовом пространстве).
- •Ряд Фурье по тригонометрической системе функций (тригонометрический ряд Фурье).
- •Лекция 2.
- •Разложение в ряд Фурье четных и нечетных функций.
- •Часть 2. Теория функций комплексной переменной. Лекция 1. Комплексные числа, 3 формы записи, основные операции.
- •Множества на комплексной плоскости.
- •Открытые и замкнутые множества, односвязное множество.
- •Лекция 2 Последовательность и ее предел.
- •Лекция 3 Геометрический смысл аргумента и модуля производной аналитической функции. Восстановление аналитической функции по ее действительной или мнимой части.
- •Восстановление аналитической функции по ее действительной или мнимой части.
- •Интеграл от функции комплексной переменной.
- •Свойства интеграла.
- •Три формы записи интеграла.
- •Интегральная теорема Коши для многосвязной области.
- •Интеграл с переменным верхним пределом.
- •Формула Ньютона – Лейбница.
- •Лекция 5. Интегральная формула Коши.
- •Лекция 6. Ряды в тфкп
- •Числовые ряды.
- •Функциональные ряды.
- •Степенные ряды.
- •Определение радиуса сходимости и исследование сходимости ряда на границе круга сходимости.
- •Лекция 8.
- •Теоремы Тейлора и Лорана
- •Теорема о разложении аналитической функции в степенной ряд
- •(Теорема Тейлора).
- •Неравенства Коши.
- •Ряд Лорана.
- •Теорема Лорана.
- •Лекция 8. Особые точки функций комплексной переменной. Правильная точка.
- •Связь полюсов и нулей.
- •Существенно особая точка.
- •Лекция 9. Вычеты и их применение.
- •Вычисление вычетов в точке конечной плоскости.
- •Общая теорема о вычетах.
- •Применение вычетов для вычисления несобственных интегралов.
- •Часть 3. Операционное исчисление Лекция 1 Преобразование Лапласа, таблица изображений.
- •Требования, предъявляемые к оригиналу.
- •Теоремы о начальном и конечном значениях.
- •Лекция 2. Теоремы запаздывания и свертки.
- •Свертка.
- •Лекция 4. Решение дифференциальных уравнений и систем Методом операционного исчисления.
- •Задано дифференциальное уравнение
- •Решение систем дифференциальных уравнений методом операционного исчисления.
- •Дополнение -функция, преобразование Лапласа -функции и ее разложение в ряд Фурье.
- •Преобразование Лапласа -функции.
Существенно особая точка.
Если вообще не
существует
![]() ,
ни конечного, ни бесконечного, то особая
точка
,
ни конечного, ни бесконечного, то особая
точка![]() называетсясущественно особой точкой
функции
называетсясущественно особой точкой
функции![]() .
.
Теорема.
Разложение функции в ряд Лорана в
окрестности существенно особой точки
конечной плоскости
![]() содержит бесконечное количество
отрицательных степеней
содержит бесконечное количество
отрицательных степеней![]() .
.
Доказательство.
Если разложение в ряд Лорана в
окрестности особой точки конечной
плоскости![]() не содержит отрицательных степеней, то
точка
не содержит отрицательных степеней, то
точка![]() - правильная (доказанная выше теорема)
- противоречие. Если разложение в ряд
Лорана содержит конечное число
отрицательных степеней, то точка
- правильная (доказанная выше теорема)
- противоречие. Если разложение в ряд
Лорана содержит конечное число
отрицательных степеней, то точка![]() - полюс (.доказанная выше теорема) -
противоречие. Остается только вариант
наличия в разложении бесконечного числа
слагаемых с отрицательными степенями.
- полюс (.доказанная выше теорема) -
противоречие. Остается только вариант
наличия в разложении бесконечного числа
слагаемых с отрицательными степенями.
Теорема
Сохоцкого.Каково бы ни было число
А, конечное или бесконечное, существует
такая последовательность
![]() -
существенно особая точка функции
-
существенно особая точка функции![]() ,
что
,
что![]() .
.
Доказательство.
1) Пусть A– конечное число.
Предположим, что не существует
последовательности, о которой идет речь
в теореме. Тогда значения функции
отделены отA, т.е.![]() .
Рассмотрим функцию
.
Рассмотрим функцию![]() .
.
Из предыдущей
оценки следует, что в
![]() -
окрестности точки
-
окрестности точки![]()
![]() ,
т.е.
,
т.е.![]() ограничена, следовательно,
ограничена, следовательно,![]() -
правильная точка функции
-
правильная точка функции![]() .
Поэтому существует конечный предел
.
Поэтому существует конечный предел![]() .
.
Пусть
 .
Выразим
.
Выразим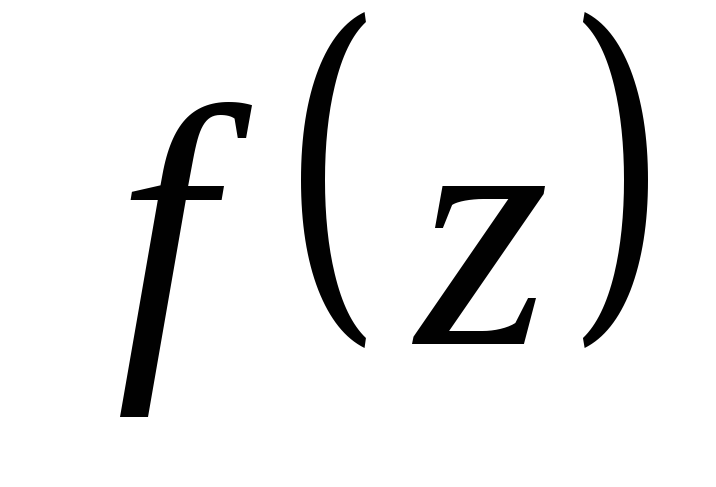 через
через .
. .
Тогда
.
Тогда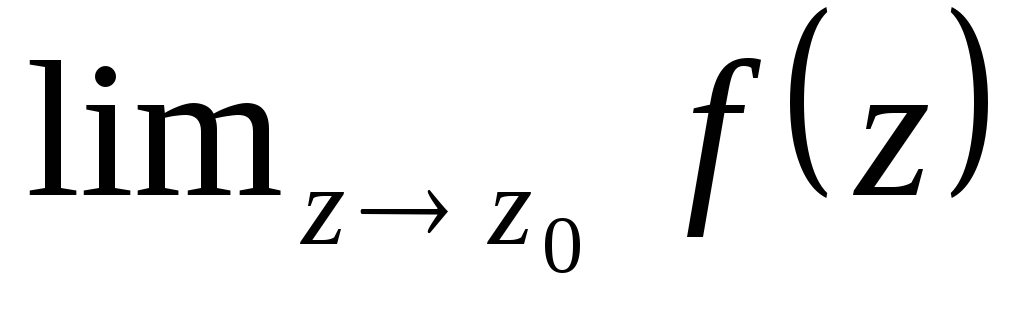 =
= - конечное число. Следовательно,
- конечное число. Следовательно, -
правильная точка функции
-
правильная точка функции - противоречие.
- противоречие.Пусть
 .
.
 .
.
Тогда
![]() ,
т.е.
,
т.е.![]() - полюс
- полюс![]() .
Противоречие.
.
Противоречие.
2) Пусть
![]() .
Надо доказать, что при
.
Надо доказать, что при![]() .
Пусть для любой последовательности
.
Пусть для любой последовательности![]() не стремится к бесконечно удаленной
точке. Тогда для любой последовательности
не стремится к бесконечно удаленной
точке. Тогда для любой последовательности![]()
![]() ,
следовательно, функция
,
следовательно, функция![]() ограничена в окрестности
ограничена в окрестности![]() ,
тогда
,
тогда![]() - правильная точка
- правильная точка![]() - противоречие.
- противоречие.
Классификация
особой точки ![]() (конечной плоскости) функции
(конечной плоскости) функции
![]() по ее разложению в ряд Лорана в окрестности
этой точки.
по ее разложению в ряд Лорана в окрестности
этой точки.
Если разложение
функции
![]() в ряд Лорана в окрестности
в ряд Лорана в окрестности![]() (по степеням
(по степеням![]() ):
):
Не содержит отрицательных степеней, то
 - правильная точка
- правильная точка .
.Содержит конечное число отрицательных степеней, то
 - полюс
- полюс ,
причем наинизшая отрицательная степень
определяет порядок полюса.
,
причем наинизшая отрицательная степень
определяет порядок полюса.Содержит бесконечное количество членов с отрицательными степенями, то
 - существенно особая точка
- существенно особая точка .
.
Это следует из доказанных выше теорем.
Классификация
бесконечно удаленной особой точки ![]()
![]() функции
функции
![]() по ее разложению в ряд Лорана в окрестности
этой точки.
по ее разложению в ряд Лорана в окрестности
этой точки.
Разложение
в ряд Лорана в окрестности точки
![]()
![]() ,
т.е. в области
,
т.е. в области![]() представляет
собой ряд Лорана по степенямz:
представляет
собой ряд Лорана по степенямz:![]() ,
в которомглавная часть, определяющая
особенности функции, содержитположительные
степени,аправильная часть–отрицательные степени.
,
в которомглавная часть, определяющая
особенности функции, содержитположительные
степени,аправильная часть–отрицательные степени.
Если
разложение в ряд Лорана в окрестности
точки
![]()
![]() ,
т.е. в области
,
т.е. в области![]() :
:
Не содержит положительных степеней, то

 -
правильная точка
-
правильная точка .
.Содержит конечное число положительных степеней, то

 - полюс
- полюс ,
причем наивысшая положительная степень
определяет порядок полюса.
,
причем наивысшая положительная степень
определяет порядок полюса.Содержит бесконечное количество членов с положительными степенями, то

 - существенно особая точка
- существенно особая точка .
.
Примеры.
 .
Это и есть разложение в ряд Лорана в
окрестности точки
.
Это и есть разложение в ряд Лорана в
окрестности точки
 ,
т.е. в области
,
т.е. в области ,
поэтому
,
поэтому
 - полюс
- полюс второго порядка.
второго порядка. .
Разложение по степеням
.
Разложение по степеням :
: справедливо
в области
справедливо
в области ,
т.е. в окрестности точки
,
т.е. в окрестности точки
 .
Оно содержит бесконечное количество
членов с положительными степенями,
поэтому
.
Оно содержит бесконечное количество
членов с положительными степенями,
поэтому
 - существенно особая точка
- существенно особая точка .
.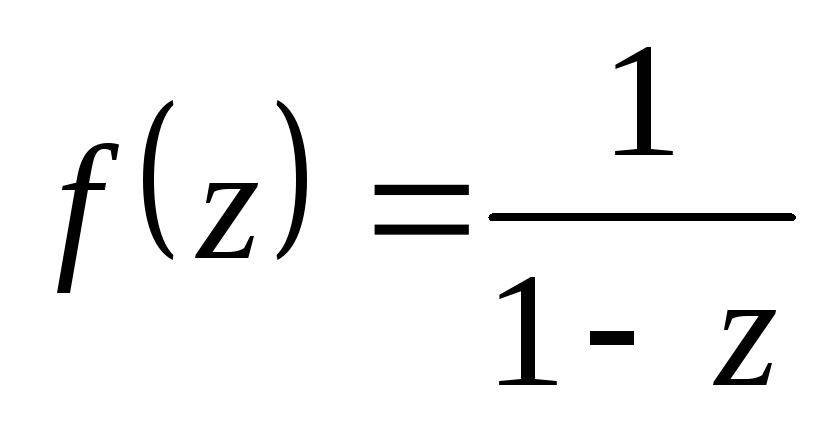 .
Запишем разложение в окрестности точки
.
Запишем разложение в окрестности точки
 ,
т.е. в области
,
т.е. в области .
.
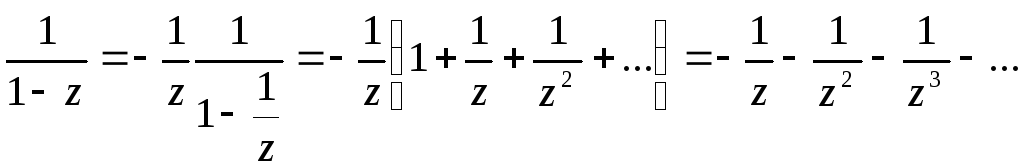 .
Разложение не содержит положительных
степеней
.
Разложение не содержит положительных
степеней![]() ,
поэтому точка
,
поэтому точка![]()
![]() - правильная, точнее, нуль первого
порядка.
- правильная, точнее, нуль первого
порядка.
4.
![]() .
Запишем разложение по степеням
.
Запишем разложение по степеням![]() в окрестности точки
в окрестности точки![]()
![]() .
.![]()
В разложении
старшая положительная степень – первая,
поэтому
![]()
![]() - полюс первого порядка. Это же разложение
справедливо в области
- полюс первого порядка. Это же разложение
справедливо в области![]() ,
поэтому оно является разложением в
окрестности точки
,
поэтому оно является разложением в
окрестности точки![]() .
В нем бесконечное количество отрицательных
степеней, поэтому точка
.
В нем бесконечное количество отрицательных
степеней, поэтому точка![]() - существенно особая.
- существенно особая.
