-
Расчёт электрической цепи переменного тока.
2
.1. В
соответствии с вариантом задания
начертим принципиальную схему
электрической цепи, также произвольно
зададим направления токов ветвей
(рис.8). Параметры элементов схемы и вид
двухполюсников указаны в таблице 2.
Рис.8.
2.2. Рассчитаем сопротивление всех ветвей электрической цепи (рис.8) и запишем в показательной и алгебраической формах.
Комплексное сопротивление ветвей, с учётом внутреннего сопротивления источников электрической энергии:
(16)
,
где
Гц.
Запишем
сопротивления ветвей в алгебраической
форме:
Ом;
Ом;
Ом; (17)
Ом;
Ом,
Учитывая данные таблицы 2, получим:
Ом;
Ом;
Ом ; 
Ом; (18)
Ом,
Запишем сопротивления ветвей в показательной форме. В общем случае комплексное сопротивление ветви в показательной форме имеет вид:
, (19)
где
(20)
,
при
; 
,
при
Используя
формулы (20), запишем комплексное
сопротивление ветвей в показательной
форме:
Ом;
Ом;
Ом; (21)
Ом;
Ом.
Определим активное и реактивное сопротивление каждой ветви:
для первой ветви:
Ом; 
Ом;
для второй ветви:
Ом; 
Ом;
для третей ветви:
Ом; 
Ом;
для четвёртой
ветви:
Ом; 
Ом;
для пятой ветви:
Ом; 
Ом;
-
Запишем основную систему уравнений электрического равновесия цепи (рис.8) для мгновенных значений токов и напряжений.
Топологические уравнения ветвей:
по первому закону Кирхгофа для мгновенных значений:
; 
;
.
По второму закону Кирхгофа для мгновенных значений:
;
;
,
где
В; 
В.
Компонентные
уравнения ветвей:
; 
; 
; 
;
; 
; 
; 
;
;
; 
; 
;
; 
.
Компонентные и топологические уравнения ветвей составляют основную систему уравнений электрического равновесия цепи.
-
Используя символический метод расчёта электрических цепей, найдём токи и напряжения всех ветвей электрической цепи (рис.9).
Рис.9.
Предположим, что
в каждом контуре протекает свой контурный
ток, комплексные амплитуды которых
равны соответственно:
(рис.9).
Запишем уравнения
по второму закону Кирхгофа для токов
.
В результате получим следующую систему
уравнений:
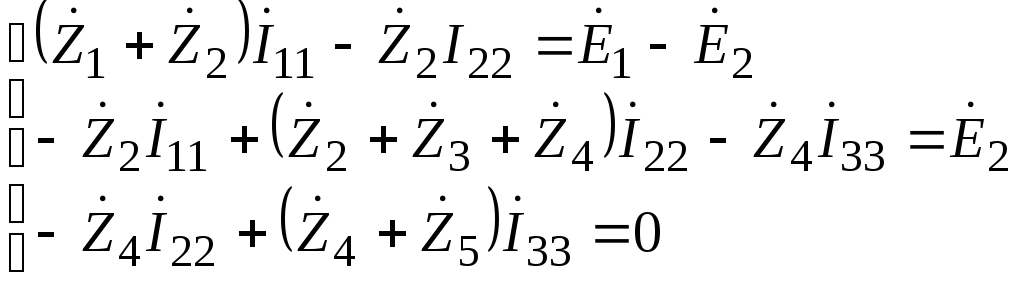, (20)
где
комплексные сопротивления ветвей
исследуемой электрической цепи (см.
формулы 18);
и
комплексные амплитуды источников
электрической энергии:
, 
. (21)
Подставляя (18) и (21) в систему уравнений (20), получим матричное уравнение:
(22)
где
; 
; 
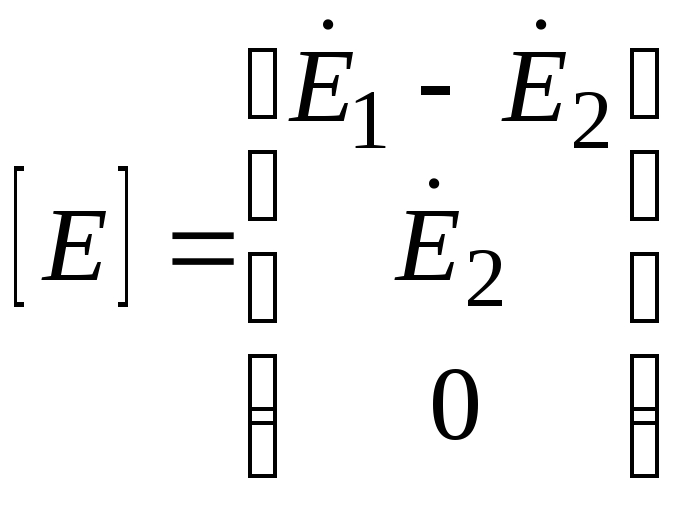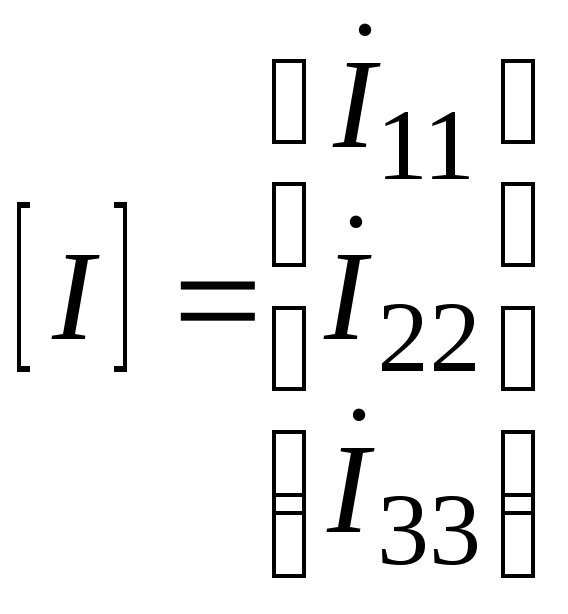
Решая матричное уравнение (22) в среде MathCad (см. приложение В), получим следующие значения контурных токов:
А;
А; (23)
А.
Найдём
комплексные амплитуды токов ветвей
электрической цепи (рис.9):
А;
А;
А; (24)
;
А.
Используя (24) определим активную и реактивную составляющие токов ветвей:
для первой ветви:
А; 
А;
для второй ветви:
А; 
А;
для третей ветви:
А; 
А;
для четвёртой
ветви:
А; 
А;
для пятой ветви:
А; 
А;
Используя формулы
перехода комплексных амплитуд к
мгновенным значениям тока и учитывая,
что циклическая частота
,
получим мгновенные значения токов
ветвей:
А;
А;
А; (25)
А;
А.
Применяя
обобщённый закон Ома для комплексных
величин, найдём комплексные амплитуды
напряжений ветвей:
;
;
; (26)
;
.
Подставляя (18), (21) и (24) в (26), получим:
;
;
; (27)
;
.
Вычисляя значения выражений (27), получим комплексные амплитуды напряжений ветвей:
В;
В;
В; (28)
В;
В.
Определим активную и реактивную составляющие напряжений ветвей:
для первой ветви:
В; 
В;
для второй ветви:
В; 
В;
для третей ветви:
В; 
В;
для четвёртой
ветви:
В; 
В;
для пятой ветви:
В; 
В;
Используя формулы
перехода комплексных амплитуд к
мгновенным значениям напряжения и
учитывая, что циклическая частота
,
получим мгновенные значения напряжений
ветвей:
В;
В;
В; (29)
В;
В.
2.5.Для
каждой ветви электрической цепи построим
полную векторную диаграмму токов и
напряжений. Для этого воспользуемся
данными, полученными в пункте 2.4. На
рис.10 представлены диаграммы токов и
напряжений ветвей электрической цепи
(рис.9). Для улучшения наглядности модули
векторов
,
увеличены в 10 раз; модули векторов
,
,
,
увеличены в 500 раз; модуль вектора
увеличен в 50000 раз.
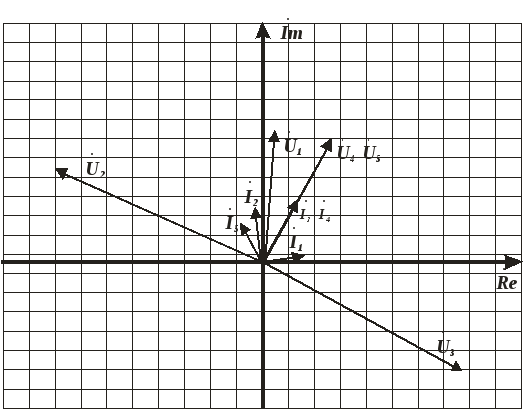
Рис.10.
2.6 Для ветвей
электрической цепи с источниками ЭДС
и
найдём комплексную, полную, активную и
реактивную мощности.
Найдём напряжения
и токи в ветвях с источниками ЭДС
и
в показательной форме. Так как:
В;
В;
А;
А,
то, пользуясь формулами (20), получим:
В;
;
В; 
А;
;
А; 
,
поэтому
В;
В;
А;
А.
Комплексная мощность равна:
, (30)
где
-
комплексно-сопряжённое значение тока
.
Так как
и
,
то комплексную мощность можно записать
в следующем виде:
(31)
Модуль комплексной мощности есть полная мощность:
(32)
Мощность, выделяющаяся на активных элементах:
(33)
Мощность реактивных элементов:
(34)
Пользуясь формулами
(30)-(34), найдём комплексную, полную,
активную и реактивную мощности в ветвях
с источниками ЭДС
и
.
В результате получим:
Для первой ветви:
комплексная мощность:
полная мощность:
;
активная мощность:
Вт;
реактивная мощность.
Вар;
Для второй ветви:
комплексная мощность:
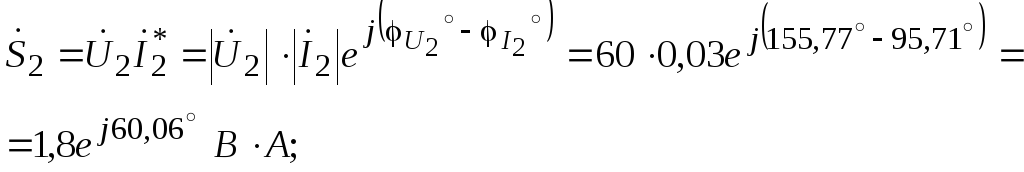
полная мощность:
;
активная мощность:
Вт;
реактивная мощность.
Вар;
2.7. Построим
графики мгновенных значений токов,
напряжений и мощностей в ветвях с
источниками ЭДС
и
.
Мгновенные значения токов и напряжений
в ветвях исследуемой электрической
цепи были найдены в пункте 2.4 (см. (25) и
(29)).
Мгновенное значение
тока ветви с источником ЭДС
:
А;
с источником
:
А.
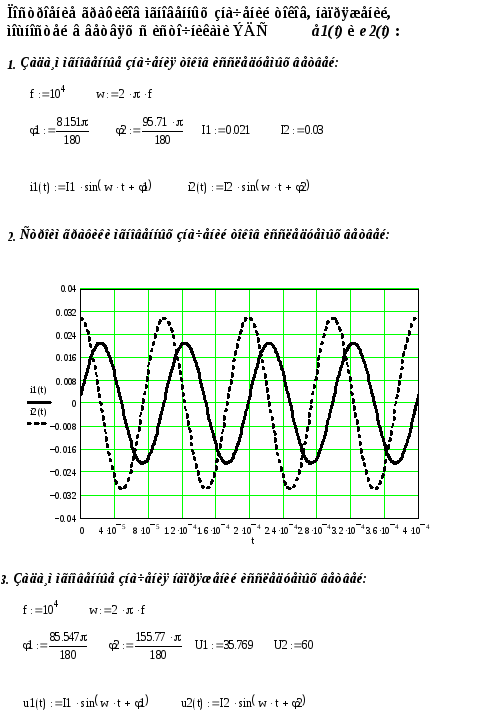
Используя среду MathCad
(см.Приложение Г), построим графики
мгновенных значений токов и напряжений
исследуемых ветвей. На рис.11 представлены
графики мгновенных значений токов
и
.
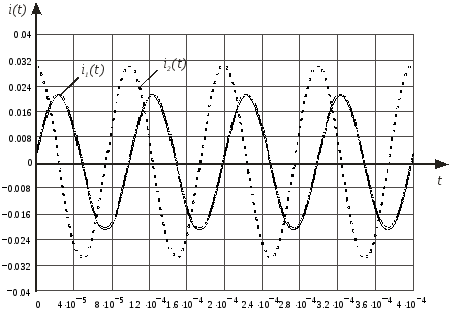
Рис.11.
Мгновенное значение
напряжения ветви с источником ЭДС
:
В;
с источником
:
В.
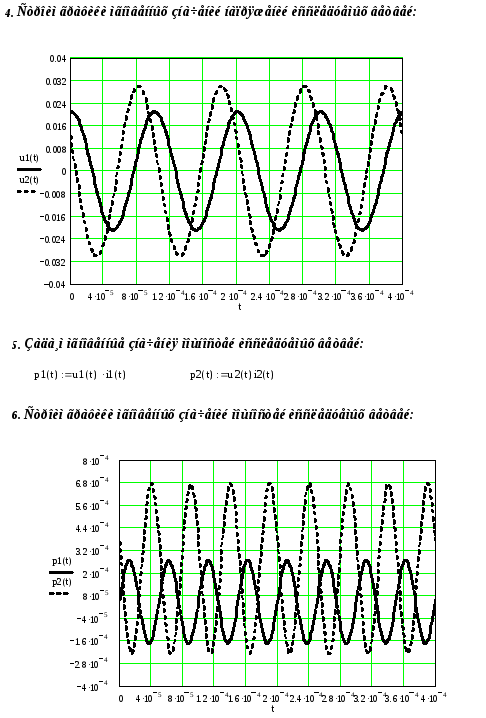
На рис.12 представлены графики мгновенных
значений напряжений
и
.
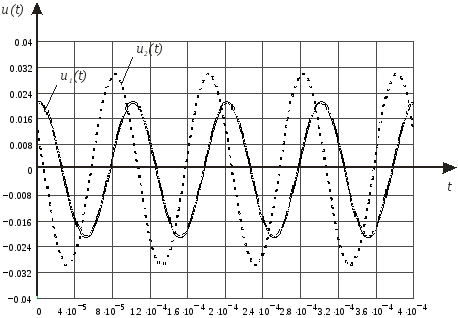
Рис.12.
Мгновенные значения мощности получим перемножением мгновенных значений токов и напряжений соответствующих ветвей (см. Приложение Г):
На рис.13 представлены графики мгновенных значений мощностей исследуемых ветвей.
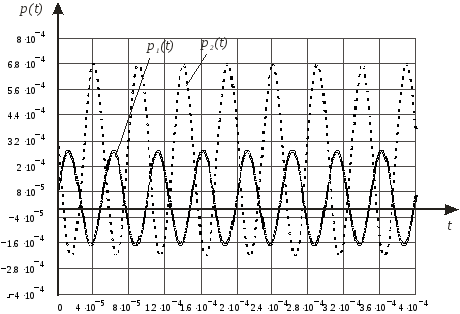
Рис.13.
Заключение
В ходе выполнения расчётно-графической работы было…
ПРИЛОЖЕНИЯ
Приложение А
Приложение Б
Приложение В
Приложение Г
