Введение
Данная расчётно-графическая работа посвящена изучению теории линейных электрических цепей. Теория линейных электрических цепей является основной теоретической базой в подготовке инженеров по радиотехнике, радиосвязи, радиовещанию, телевидению и другим специальностям. Данная расчётно-графическая работа...
-
Расчёт электрической цепи постоянного тока
1.1. В соответствии с вариантом задания начертим принципиальную схему электрической цепи (рис.3,а). Параметры элементов схемы указаны в таблице 1.
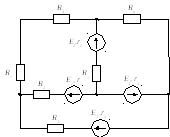
а)
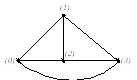
б) в)
Рис.3.
1.2. Построим граф исследуемой электрической цепи, используя сокращённое и расширенное топологические описания.
На рис.3,б-в представлены графы схемы электрической цепи (рис.3,а) с сокращённым и топологическим описаниями соответственно.
1.3. Рассчитаем
токи и напряжения ветвей схемы
электрической цепи (рис.4) методом
контурных токов. Для этого, предположим,
что в каждом контуре протекает свой
контурный ток:
,
,
(рис.4).
Рис.4
Составим уравнения по второму закону Кирхгофа для контурных токов, с учётом внутреннего сопротивления источников напряжения.
Для первого контура:
. (1)
Для второго контура:
. (2)
Для третьего контура:
. (3)
В уравнениях (1) –
(2) раскроем скобки и сгруппируем слагаемые
по
,
,
.
В результате получим систему уравнений
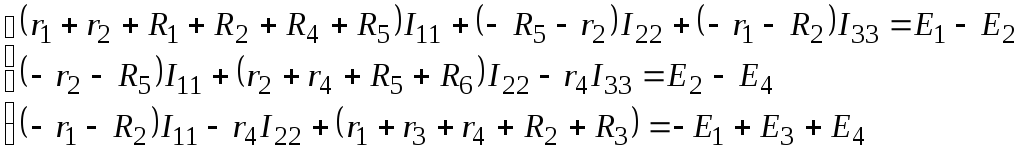(4).
(4)
Решим данную систему уравнений матричным методом. Для этого произведём в (4) следующую замену:
; 
; 
;
; 
;
; 
; 
;
; 
; 
.
В результате получим:
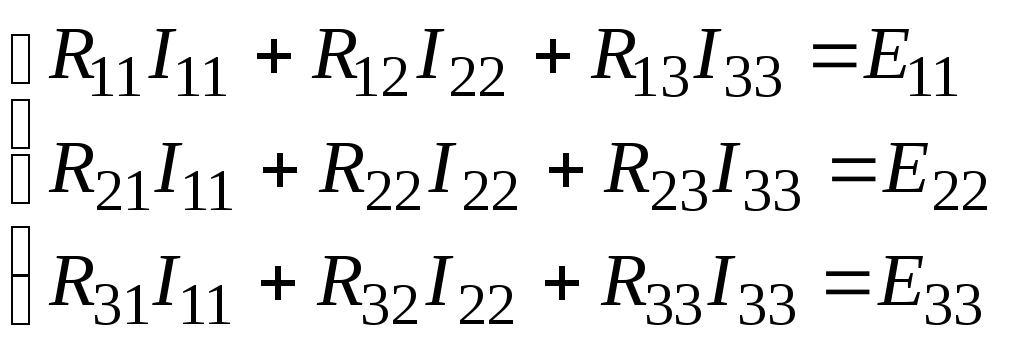, (5)
или в матричном виде:
, (6)
где
; 
;
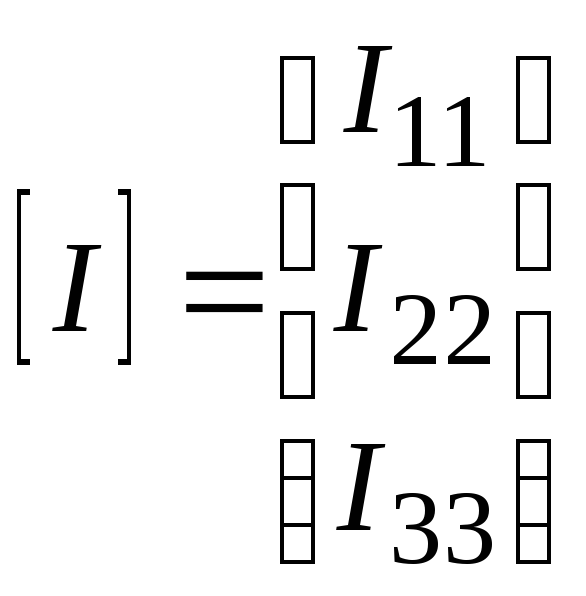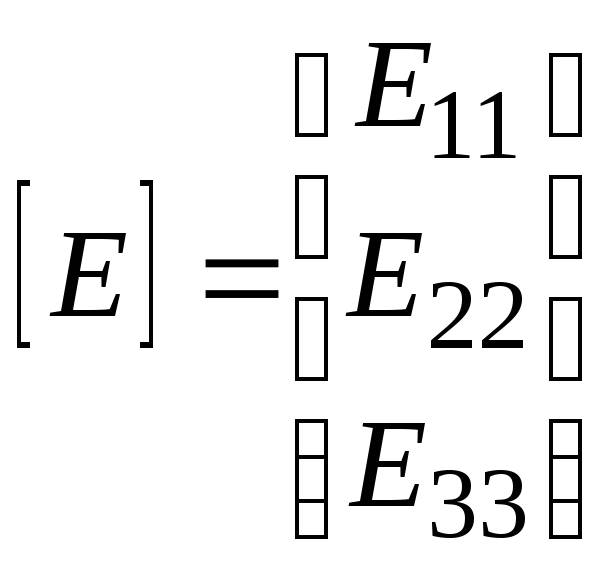(7)
Учитывая данные таблицы 1, получим:
;
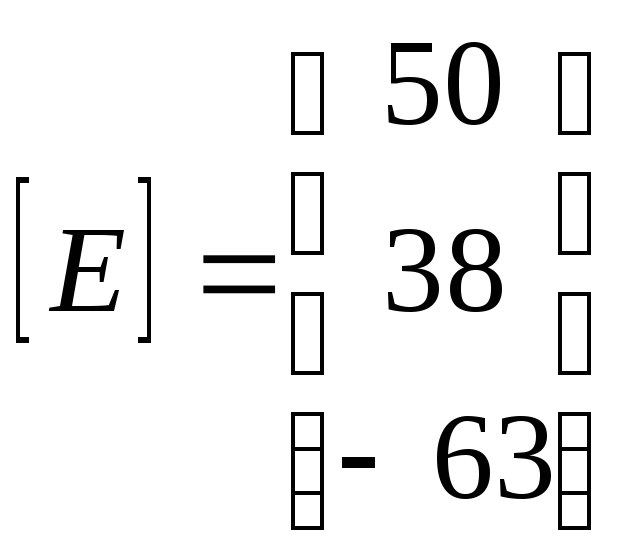
Рассчитаем токи
,
,
в среде MathCad
(см. приложение А). Получим следующие
значения контурных токов:
А; 
А; 
А.
Найдём токи в ветвях электрической цепи (рис.4).
; 
; 
;
(8)
; 
; 
Таким образом:
А; 
А;
А; 
А;
А; 
А.
На рис.5 указаны
положительные направления токов
,
,
,
,
,
,
значения которых равны соответственно
,
,
,
,
,
.
Рис.5
Найдём напряжения ветвей схемы электрической цепи (рис.5) по обобщённому закону Ома:
(9)
Таким
образом, напряжения ветвей равны:
В;
В;
В;
В;
В;
В.
На рис.5 указаны
положительные направления напряжений
ветвей
,
,
,
,
,
,
значения которых равны
,
,
,
,
,
.
1
.4. Рассчитаем
токи и напряжения ветвей схемы
электрической цепи (рис.6) методом узловых
потенциалов.
Рис.6.
Для этого найдём потенциалы узлов схемы (рис.6). Примем потенциал узла 0 равным нулю и найдём потенциалы всех оставшихся узлов. Согласно методу узловых потенциалов, составим следующую систему уравнений:
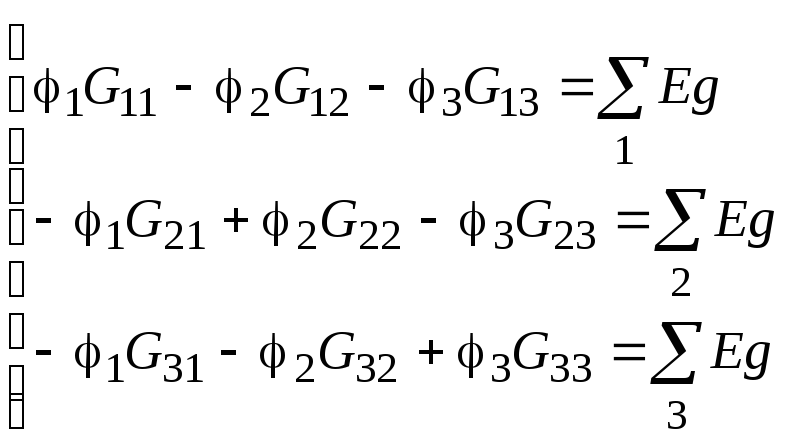, (10)
где
Запишем систему уравнений (10) в матричном виде:
, (11)
где
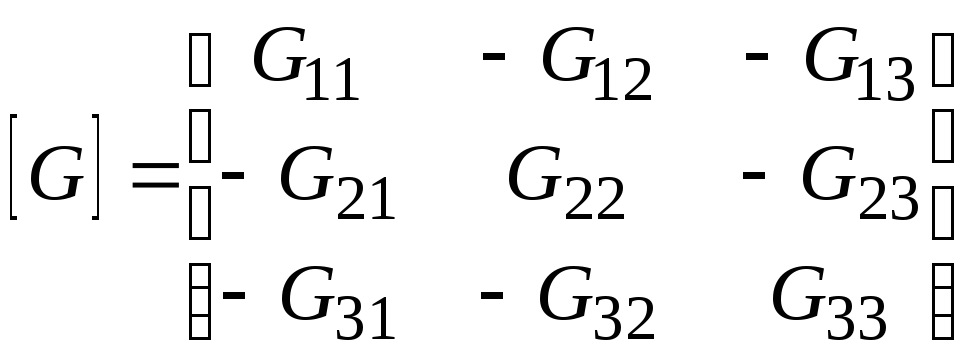
Решим уравнение (11), используя среду MathCad (см.приложение Б). Получим следующие значения узловых потенциалов:
В; 
В; 
В (12)
Найдём напряжения ветвей электрической схемы:
В;
В;
В;
В;
В;
В.
Используя обобщённый закон Ома для участка цепи, рассчитаем токи ветвей:
А;
А;
А;
А;
А;
А.
Рис.7.
На рис.7 показаны положительные направления токов и напряжений ветвей.
1.5. Определим мощность потерь и коэффициент полезного действия электрической цепи (рис.7), пренебрегая сопротивлением проводов.
Будем считать полезной нагрузкой все сопротивления электрической цепи, кроме внутренних сопротивлений источников электрической энергии. Также учтём следующее: если направление тока ветви совпадает с направлением источника ЭДС ветви, то источник вырабатывает электрическую энергию. Если же направление тока противоположно направлению ЭДС, то источник работает в режиме потребителя и является приёмником электрической энергии. Мощность, которую потребляет источник энергии, будем считать полезной. Тогда полезная мощность будет равна:
, (13)
откуда
Мощность
потерь будет равна мощности, которая
выделяется на внутренних сопротивлениях
источников энергии:
, (14)
откуда
.
Полная мощность цепи равна мощности, которую отдают источники электрической энергии в цепь:
, (15)
откуда
Найдём
коэффициент полезного действия цепи:
