3.3. Алгоритм нахождения компонент связанности

Вершины Х_i и X_j слабо связны, если существует путь (Х_i и X_j) в графе (G,X).

Вершины X_i и X_j сильно связаны, если существуют пути (Х_i и X_j) и (X_j и Х_i) в графе (G, X).

Если в графе нет путей Х_i и X_j и нет обратного пути из Х_j в X_i, то вершины Х_i и X_j не связаны.

Для неориентированною графа имеет смысл только понятие сильной связности. Отношение связности рефлексивно, симметрично, транзитивно - является отношением эквивалентности и однозначно разбивает множество вершим графа на компоненты связности: максимальные подмножества сильно связанных между собой вершин.

Пример 3.2.1

Компоненты связности: 1) {x1, x2, x3, x4}; 2) {x5, x6, x7}; 3) {x8}.

Между компонентами - только слабая связность: есть пути из вершин компоненты 1) в вершины компоненты 2) и 3) и из вершин компоненты 2) в 3).

3.2.1. Алгоритм построения компонент связности в неориентированном графе

1. i=0. Все вершины графа не отмечены.

2. i=i+1. Выбираем очередную неотмеченною вершину, отмечаем ее и все связанные с нею вершины значением индекса i с помощью распространения волны отметок по ребрам, идущим от уже отмеченных индексом i вершин. Таким образом, выделяется i компонента связности. Если есть еще неотмеченные вершины, то выполняется п. 2, иначе выделение компонент связности закончено.

П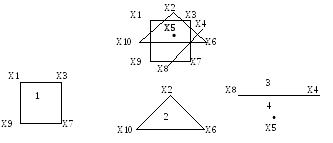 ример 3.2.2

1.i = 0

2. i = 1. Отмечаем индексом i =1 вершину Х₁, и связанные с ней вершины

Х₃, Х₇, Х₉. Получена первая компонента связности: 1{ Х_1, Х₃, Х₇, Х₉}.

3. i =2. Отметим индексом i = 2 вершину Х₄ и вершины Х₆, Х₁₀. Построена

вторая компонента связности: 2{ Х₂, Х₆, Х₁₀)

4. i=3 Отмечаются индексом i = 3 вершины X₄ и Х₈. Построена третья

компонента связности: 3{X₄, X₈}.

5. i=4. Отметим индексом i = 4 вершину Х₅, которая формирует четвертую компоненту связности -{X₅}.

3.4. Дерево. Остов.

Д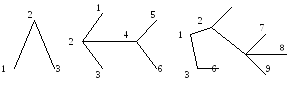 еревом называется конечный связный граф без циклов. Из свойств связности и отсутствия циклов следует, что у дерева количество компонент связности р =1 и цикломатическое число  = 0 = m – n + 1, отсюда следует что m = n -1 ; т.е. число ребер в дереве на единицу меньше числа вершин. Ниже приведены примеры деревьев.

4

Рис.3

Остов – это подграф (частичный), который может быть построен из графа удалением некоторых ребер и который является деревом.

В общем случае для графа можно построить несколько остовов. Для приведенного ниже графа построен один из возможных вариантов остова.

Д ля несвязного графа рассматриваются отдельные его компоненты. Остов такого графа – совокупность его компонент.

3.4.1. Алгоритм построения произвольного остова

1. Для каждой компоненты i графа выполняем пп.2 и 3.

2.Строим частичный подграф, содержащий все n_i вершины компоненты и не содержащий ребер (0 граф).

3. Если в текущий частичный граф включены уже n_i-1 ребер, то остов для компоненты i построен, иначе выбираем очередное нерассмотренное ребро компоненты и пытаемся включить его в текущий граф. Если в текущем графе это не приводит к образованию цикла, то включаем ребра, иначе - не включаем. Ребро считаем рассмотренным.

Выполняем п. 3.

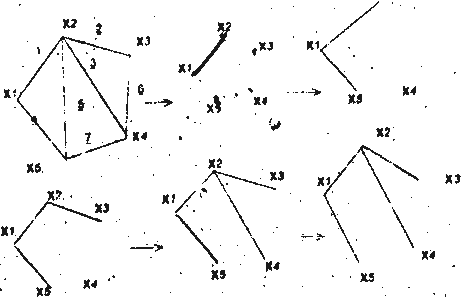
Так как цикл не образовался, то все ребра с номерами 1, 2, 3, 4 включены в остов. Проверяем: m=n-1(4-5-1).