2.7. Многокритериальные задачи исследования операций. О проблеме формирования единого критерия эффективности.

Как мы помним, операция есть целенаправленное меропри­ятие, и формальным выражением этого является сущест­вование некоторого функционала W — критерия эффек­тивности, увеличение (или уменьшение) которого и отражает стремление к достижению цели операции. Это, так сказать, в теории. А на практике, как мы убедились, проблема формирования критерия зачастую представляет собой чрезвычайные трудности. Эти трудности, как мы отметили ранее, существенно возрастают по мере усложнения и укрупнения изучаемых проблем, в результате возникновения ситуации, когда формальное описание единого критерия эффективности как эквивалента цели не только затруднительно, но, зачастую, в принципе невозможно.

Во всех подобных случаях попытки конкретизировать цель выливаются обычно в составление некоторого списка требований, состоящего из набора частных показателей эффективности (критериев) u_i (x, y), ( i = 1, n), сово­купное увеличение или уменьшение которых и представляется оперирующей стороне целью операции. Здесь и далее у = (y₁, y₂, …, y_n) - вектор управлений, х = (х₁, х₂, …, х_m) - вектор неопределенных параметров, X и Y –соответственно множества их возможных реализаций.

Эти частные показатели (критерии) U_i могут отражать оценки различных свойств объекта или процесса исследования или оценки одной и той же характеристики, но с различных точек зрения. Как правило, эти критерии оказываются несогласованными, то есть, увеличение одних из них может привести к уменьше­нию других, что делает проблему оптимального выбора про­тиворечивой и неоднозначной.

Такие задачи исследования операций, в которых цель опера­ции выражается столь неопределенно, что не может быть отражена в едином критерии эффективности, обычно на­зывают многокритериальными. Формально многокритериальная задача определяется множеством допустимых решений Х, на котором целевые функции u_i (x, y), (i=1, n) принимают действительные значения.

Сущность многокритериальной задачи состоит в нахождении такого решения х  Х, которое в том или ином смысле максимизирует значения всех функций u_i.

Существование решения, буквально максимизирующего все целевые функции, является редким исключением. Поэтому в теории многокритериальных задач понятие оптимальности получает различные и притом нетривиальные истолкования. Решение, обращающее в максимум один из показателей, например, u₁, как правило, не обращает ни в максимум, ни в минимум другие показатели u₂, u₃, …

[24/с.24] Однако, количественный анализ эффективности может оказаться весьма полезным и в случае нескольких показателей эффективности. Прежде всего, он позволяет заранее отбросить явно нерациональные варианты решений, уступающие лучшим вариантам по всем показателям.

Проиллюстрируем сказанное на примере. Пусть анализируется некоторая система, оцениваемая по двум показателям:

W – эффективность выполнения задачи системы;

C – затраты на создание системы.

Очевидно, что первый показатель желательно обратить в максимум, второй – в минимум. Предположим для простоты, что предлагается на выбор конечное число – 20 различных вариантов решения; обозначим их x₁, x₂, …, x₂₀

Д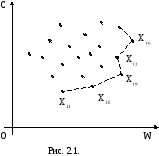ля каждого из них известны значения обоих показателей W и S.

Изобразим для наглядности каждый вариант решения в виде точки на плоскости с координатами W и S (рис. 2.1).

Из рисунка видно, что некоторые варианты решений «неконкурентоспособны» и заранее могут быть отброшены.

Действительно, те варианты, которые при той же стоимости S имеют преимущество над другими вариантами по эффективности W, должны лежать на правой границе области возможных вариантов. Те же варианты, которые при равной эффективности обладают меньшей стоимостью, должны лежать на нижней границе области возможных вариантов.

Очевидно, что при оценке по этим двум показателям следует предпочесть те варианты, которые лежат одновременно и на левой, и на нижней границе области (см пунктирную линию на рис. 2.1). Действительно, для каждого из вариантов, не лежащих на этом участке границы, всегда найдется другой вариант, не уступающий ему по эффективности, но зато более дешевый или, наоборот, не уступающий ему по дешевизне, но зато более эффективный.

Таким образом, из 20 предварительно выдвинутых вариантов большинство выпадает из рассмотрения, для дальнейшего анализа остаются только пять: x₁₀, x₁₁, x₁₂, x₁₆ и x₁₉. Из них x₁₆ - наиболее эффективный, x₁₁ - самый дешевый. Задача лица, принимающего решение, - разобраться в том, какой ценой мы согласны оплатить повышение эффективности или, наоборот, какой долей эффективности мы согласны пожертвовать, чтобы не нести слишком больших материальных потерь.

Аналогичный предварительный просмотр вариантов (правда без такой наглядной геометрической интерпретации) может быть произведен и в случае многих показателей.

Такая процедура предварительной отбраковки неконкурентоспособных вариантов решения должна всегда предшествовать решению задачи выбора целесообразного варианта с несколькими показателями.

Комплексная оценка системы сразу по нескольким показателям затруднительна и требует размышлений. Поэтому в теории многокритериальных задач понятие оптимальности получает различные и притом нетривиальные истолкования. Содержание многокритериальных задач состоит в выработке таких концепций оптимальности, доказательстве их реализуемости и нахождении этих реализаций.

* * * * * * * * * * * * * * * * * * * * * * * * * * *

Существует несколько способов борьбы с многокритериальностью.

А. Одним из распространен­ных, но, к сожалению, малоэффективных способов борьбы с многокритериальностью является, так называемое, свертывание частных критериев в некоторый единый критерий эффективности путем замены системы целевых функций u_i одной «сводной» функцией W(u_i). Эффективной эта процедура бывает лишь тогда, когда оперирующая сторона подсознательно ощу­щает единство целей операции, и задача исследователя опе­рации - перевести это подсознательное ощущение в кон­кретную осознанную форму. В противном случае такая процедура к успеху не приводит и привести не может, так как объективного единства целей в операции не существует. Проблема оптимального выбора в этом случае не мо­жет быть решена формальными средствами, она становится проблемой чисто психологической. Некоторые наиболее распространенные способы свертывания частных критериев:

1. Формирование цели качественного типа. Под качественными целями понимаются цели, которые могут быть только или достигнуты, или не достигнуты. Считается, что все результаты операции, приводящие к достижению цели, одинаково хороши (без их ранжирования между собой); точно так же все результаты, не приводящие к достижению цели, одинаково неудовлетворительны. При этом критерий эффективности должен принимать только два значения: например, 1 – в случае успеха и 0 - в противоположном случае или 1 и -, если нужно подчеркнуть полную неприемлемость недостижения цели;

Свертывание частных крите­риев в качественный осуществляется разбиением множе­ства значений частных критериев на удовлетворительные и неудовлетворительные. Назначаются некоторые числа u_i⁰ (i = 1, n) и удовлетворительными значениями объявляются только такие критерии, для которых u_i (x, y)  u_i⁰, i = 1, n.

При этом критерий - свертка принимает вид:

(2.1)

Этот способ образования единого критерия наиболее доступен пониманию оперирующей стороны, так как ближе всего отражает смысл требований, налагаемых на зна­чения частных критериев. Однако трудности корректного назначения чисел u_i⁰ так, чтобы не потерять наиболее эф­фективные способы действий или не попасть в область не­достижимых значений, делают эту процедуру не менее противоречивой и неоднозначной, чем стремление к одно­временному увеличению значений всех частных критериев.

2. Логическое свертывание. Если частные критерии u_i (x, у) являются критериями качественного типа, прини­мающими только значения 0 или 1, то для их свертывания можно использовать логические операции:

а) конъюнкция. Единая цель состоит в выполнении всех частных целей:

(2.2)

б) дизъюнкция. Единая цель, состоит в выполнении хо­тя бы одной из частных целей: (2.3)

Это наиболее конструктивный способ свертывания частных критериев. Однако он имеет ограниченное примене­ние, так как годен только для качественных целей.

3. Обобщенное логическое свертывание. Прямым обоб­щением действий предыдущего пункта является вместо (2.2):

(2.4)

вместо (2.3): (2.5)

Эти способы свертывания применимы для любых типов критериев. Выражение (2.4) немедленно превращается в (2.2), если все u_i, (x, y) принимают только значения 0; 1, а весовые коэффициенты λ_i =1. Точно так же в этом случае (2.5) эквивалентно (2.3). Трудности, связанные с таким типом свертывания, обусловлены неопределенностью при выборе конкретных значений весовых коэффициентов λ_i. Однако, подобного типа свертки могут оказаться чрезвычайно полезными при решении сложных задач те­ории исследования операций.

4. Линейное свертывание. Единый критерий эффектив­ности представляют в виде линейной комбинации частных показателей:

(2.6)

Этот способ обычно называют экономическим способом свертывания, так как весовые коэффициенты λ_i часто вы­ступают в роли цен на i-й товар и критерий W представляет собой суммарную прибыль. Назначение конкретных зна­чений коэффициентов λ_i, как и в способе 3, также вызывает немалые затруднения. Для установления значений коэффициентов λ_i нередко рекомендуется прибегать к экспертным оценкам.

Б. Другим подходом к решению многокритериальной задачи является понижение размерности задачи, при котором на каком-то этапе подготовки решений, оцениваемых по нескольким критериям, неизбежно приходится либо их ранжировать, либо отдавать предпочтение одному из этих критериев, добиваясь приемлемого компромисса. Вопрос состоит в том, каким способом и в какой форме осуществляется выбор подходящего критерия.

Существуют различные способы оценок, но первостепенное значение имеют два из них:

а) формирование множеств доминирующих решений – множества Парето, основанное на непосредственном вычислении значений критериев u_i для каждого управления с отбрасыванием бесперспективных вариантов и выбором доминирующего управления;

б) последовательный выбор уступок, связанный с исследованием задачи оптимизации по каждому из критериев u_i с одновременным изменением ограничений на величины остальных критериев.

Рассмотрим эти способы подробнее.

Формирование доминирующих решений. Предположим, что известны допустимые управления х = (х₁, х₂, …, х_m) оперирующей стороны и есть возможность вычислить значения частных критериев u₁, u₂, … u_n для каждого из управлений (табл. 2.1).

Таблица 2.1.

	u1	u2	. . .	un
x1	u1(x1)	u2(x1)	. . .	un(x1)
x2	u1(x2)	u2(x2)	. . .	un(x2)
. . .	. . .	. . .	. . .	. . .
xs	u1(xs)	u2(xs)	. . .	un(xs)
. . .	. . .	. . .	. . .	. . .
xk	u1(xk)	u2(xk)	. . .	un(xk)
. . .	. . .	. . .	. . .	. . .
xm	u1(xm)	u2(xm)	. . .	un(xm)

Рассмотрим два значения управления х_s и х_k. Будем говорить, что управление х_s доминирует над управлением х_k в смысле векторного критерия U(x)={u₁ (x), u₂ (х),…, u_n (x)}, если u_i (х_s)  u_i (х_k) (в задачах на max), причем хотя бы для одного значения i имеет место строгое неравенство. Очевидно, что из двух управлений х_s и х_k доминирующее управление х_s будет предпочтительнее в силу стремления оперирующей стороны к увеличению значений всех частных критериев (записывают x_sDx_k). Таким образом, управление х_k может быть исключено из дальнейшего анализа.

Процедуру отсева неконкурентных значений х можно продолжать до тех пор, пока она не при­ведет к выделению множества Х_ значений управления х, не сравнимых в смысле указанного принципа доминирования. Формально это означает, что для любой пары х_s и х_k  Х условие u_i (х_s)  u_i (х_k) влечет за собой равенство u_i (х_s)=u_i (х_k) для всех i. Множество Х_ называется множеством эффективных (или оптимальных по Парето) управлений, а соответствующее им множество U_= u (Х_) векторов — эффективными, или паретовскими векторами.

Управления (стратегии), признанные доминирующими, подлежат дальнейшему анализу – сравнению между собой по новым дополнительным критериям. Этот способ, конечно, не даст окончательного ответа на вопрос о лучшей стратегии, но позволит сузить круг исследуемых стратегий за счет «отсеивания» заведомо «слабых» стратегий и, тем самым, существенно сократить объемы и время исследовательской работы.

Последовательный выбор уступок. Несколько иной подход к проблеме многокритериальности вытекает из идеи последовательных уступок.

Пусть u₁, u₂, … u_n расположены в порядке убывающей важности.

Вначале отыскивается решение, доставляющее максимум показателю u₁ (max u₁ = u₁^*) при произвольных значениях других критериев, после чего оперирующая сторона ставится перед выбором – либо сохранить достигнутое, либо попытаться улучшить другие критерии (в первую очередь u₂) за счет уступок u₁*, то есть, возникает новая задача: найти решение, доставляющее экстремум u₂ при u₁≥ u₁* - Δu₁ и произвольных u₃, … u_n (здесь Δu₁ - конкретное количественное выражение уступки).

Далее ситуация повторяется: находим решение, доставляющее экстремум u₃ при u₂ ≥ u₂*- Δu₂, помня при этом об ограничении на u₁. И так далее. В результате многокритериальная задача сводится к однокритериальной путем наложения ограничения на все u_i, кроме одного, принимающего экстремальное значение.

Решая данную задачу поиска компромиссных решений, получим некоторую ясность в вопросах взаимосвязи критериев, соотношения уступок и выигрышей, влияния учтенных факторов на результат, что приведет к лучшей информированности оперирующей стороны об ожидаемых исходах планируемой операции и обеспечит более качественную подготовку окончательных решений.