
Задача № 3 (Схема №3)
Определить реакции опор балки, нагруженной, как показано на рисунке, а также построить эпюры поперечных сил Q и изгибающих моментов M.
F1 M
q
Дано: F1 = 12 кH
F2 = 8 кH
M = 20 кH·м









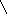
q
= 6 кH/м
с =
1,5 м 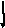

b = 2, м а = 1.4 м
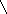
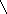
F2 Найти: RA, RВ
c b a



Решение: Рассматриваем систему сил, действующую на балку, и освобождаем точки A и C от связей, заменяя связи силами реакций связей RA и Rc . Действующую на балку равно распределенную нагрузку интенсивностью q заменяем равнодействующей Q = 1,4·q = 8400 кH, расположенной в середине длины этой нагрузки AB. Таким образом, на балку действует пара сил с моментом М и система параллельных сил F1, F2 , RA, Rc , Q. Для определения неизвестных реакций связей балки RA и Rc составляем уравнения равновесия.
RА
F1
M Rв Q 




А С
B F2
1
,5 2
1,4

z 1
z2


z 3

∑MА (Fi) = 0 RВ ·(b +c) – M + F1·с – Q·( b+ c+ a /2) + F2 · (b+ c+ a) = 0
∑MВ (Fi) =0 – M + F1·( b+ c) + F2· a - Q·( a/2) - RA ·(b+c) = 0
RВ = (M + F1·c – F2·( b+ c+ a ) + Q·(b+ c+ a/2) )/(b +c)
RВ = (20000+ 12000·1,5 – 8000·4,9 + +8400·4.2 )/3,5 =9737,143 Н
RА = F2·a – Q·( a/2) – M + F1·с
RА = 8000·1,4 – 8400·1,4/2 – 20000 +12000·2 = 2662,857 H
Возьмем для проверки уравнение равновесие сил относительно оси у
∑Fiy=0
RA-Q-F1 +F2+RB=0
2662.857-8400+8000-12000+9737.143=0
ОТВЕТ: RA = 2662,857 H RB = 9737.143 H
Для построения эпюр поперечных сил Q и изгибающих моментов M представим балку, состоящую из 3-х участков AB, BC и CD. Определим значения поперечных сил для каждого участка балки.
2663
На первом участке выберем сечение,










отстоящее на расстоянии x1 от конца балки.
400

Q 1
= RA
= 2662,857 H
















Определим
значение поперечных сил
на втором участке х2

Q2 = – F2 + q·z2
- 9337
-8000
Возьмем два крайних значения х2 для
второго участка.
z2 = 0 Q2 = – F2 + q∙0= – 8000 Н
z2 = 1,4 Q2 = – F2 + q∙1 ,4 = 400 Н
23994 Найдем
точку перегиба = - F2
+q∙ z2=0 

5320 х2=8000/6000=
1, 3 3 м

3994
Рассмотрим третий участок:





Q3 = RА
– F1
=2662, 85 –
12000 = -9337, 14.














Определим значения изгибающих
моментов 
для каждого участка балки. Воспользуемся
теми же участками и сечениями.
M1 = RA ·z1
при
z1
= 0 M1
= 0
при z1 = 1,5 M1 = 3994,228
M2 = F2 ·z2 - q·x22/2
при z1 = 0 M2 = 0
при z3 = 1,4 M2 = 8000∙ 1, 4 - 6000∙1, 42 /2= 5320
M3 = RA · z3 + M - F1·(z3 – z1 )
при z1 = 1,5 при z3 = 1,5 M3 = 2662,85 ∙ 1,5 +20000=23994,27 при z1 = 1,5 при z3 = 3,5 M3 =2662,85 ∙ 3,5 - 12000∙2+20000 = 5320
Поперечное сечение
a
=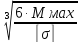 =
= =0,
1063
=0,
1063
