
- •§ 1. Пространство и его подмножества
- •§ 2. Функция n переменных, ее предел и непрервность
- •§ 3. Частные производные и дифференциал функции n, n2,
- •Обозначают введенную этим определением частную производную символами fх′(m0) или fх′(x0,y0) , а также
- •§ 4. Неявные функции.
- •§ 5. Свободный экстремум функции нескольких переменных
- •Пусть , а - любое, удовлетворяющее условиям . Взяв , удовлетворяющее указанным условиям, выберем для этого число такое, что и обозначим: . Имеем: , причём ;
- •§ 6. Условный экстремум
- •6. 3. Метод Лагранжа
- •В силу инвариантности формы первого дифференциала имеем:
- •Литература
- •§ 1. Пространство и его подмножества
- •Пространство …………………………. 3
- •§ 2. Функция n переменных, её предел и непрерывность
- •§ 3. Частные производные и дифференциалы
- •§ 4. Неявные функции
- •§ 5. Свободный экстремум функции нескольких переменных
- •§ 6. Условный экстремум
§ 3. Частные производные и дифференциал функции n, n2,
переменных
-
Частные производные функции двух переменных в точке
Пусть
функция f
определена в окрестности U![]() точки
М0 (х0,у0).
Положим φ(х)
= f(
х,у0).
Этим равенством функция φ определена
для тех х, для которых точка М(х,у0)
принадлежит U
точки
М0 (х0,у0).
Положим φ(х)
= f(
х,у0).
Этим равенством функция φ определена
для тех х, для которых точка М(х,у0)
принадлежит U![]() , т.е. φ определена в некоторой окрестности
U
, т.е. φ определена в некоторой окрестности
U![]() =(
a,b
), где
a<x0<b.
=(
a,b
), где
a<x0<b.
Определение 1. Если существует производная φ′(х0), то это число называют частной производной функции f по аргументу х в точке М0 .
Обозначают введенную этим определением частную производную символами fх′(m0) или fх′(x0,y0) , а также
Таким образом,
![]()
Пример
1.
![]() Функция f
определена
этим равенством во всех точках плоскости
Функция f
определена
этим равенством во всех точках плоскости
![]() ,
за исключением начала координат О(0,0).
Пусть М0
(х0
,у0)
– некоторая точка, отличная от О. Найдем
fх
′(M0).
Имеем:
,
за исключением начала координат О(0,0).
Пусть М0
(х0
,у0)
– некоторая точка, отличная от О. Найдем
fх
′(M0).
Имеем:
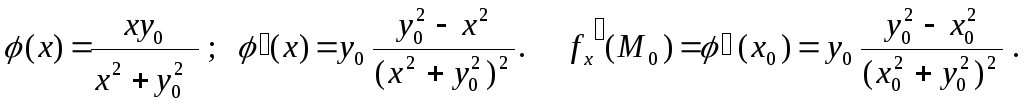
Из
свойств производной φ′
вытекают свойства частной производной
![]() :
пусть функции f
и
g
определены
в окрестности точки М0
и пусть существу- ют производные
:
пусть функции f
и
g
определены
в окрестности точки М0
и пусть существу- ют производные
![]() (M0)
и
(M0)
и
![]() (M0)
; тогда
(M0)
; тогда
-
существует hх′(M0), где h= f + g, причем hх′(M0) = fх′(M0) + gх′(M0) ;
2) существует hх′(M0), где h= f g, причем
hх′(M0) = fх′(M0) g(M0) + f(M0) gх′(M0) ;
3)
если g(M0)
≠ 0, то существует hх′(M0),
где h=
![]() ,
причем
,
причем
hх′(M0)
=

Рис.3













G

 Выясним
геометрический смысл числа
Выясним
геометрический смысл числа
 fх′(M0).
Пусть G есть
график функции f,
fх′(M0).
Пусть G есть
график функции f,
т.е. поверхность с уравнением z =f(x,y).
Обозначим через Г линию пересечения

![]() G с
плоскостью у = у0.
Уравнение Г
G с
плоскостью у = у0.
Уравнение Г
запишем в виде
системы
![]() .
.
![]() Исключив из этой
системы у,
Исключив из этой
системы у,
получим уравнение линии γ -
проекции Г на плоскость ХОZ : z = f(x,y0) = φ(x)
(рис.3). Производная φ′(х0) есть тангенс угла наклона к оси абсцисс касатель- ной l к кривой γ в точке Р0 , абсцисса которой равна х0 . Заметим, что кривые γ и Г конгруентны (получаются одна из другой параллельным переносом), а Р0 есть проекция точки N0(x0,y0,z0), где z0=f(x0,y0) . Значит, касательная L к кривой Г в точке N0 параллельна касательной l к γ в точке Р0. Отсюда заключаем: пусть Г есть линия пересечения графика функции с плоскостью, проходящей через точку М0 перпендикулярно к оси ординат, а N0 - точка на Г, проекция которой на ХОУ есть М0; частная производная fх′(M0) равна тангенсу угла между осью абсцисс и касательной к Г, проведенной в точке N0.
Аналогично
определяется fу′(M0)
– частная производная функции f
по аргументу
у в
точке М0(х0,у0):
fу′(M0)
![]() ψ′(у0)
, где ψ(у)
= f(x0,y).
ψ′(у0)
, где ψ(у)
= f(x0,y).
Пример
2.
![]() .
Найдем fу′(M0),
где М0(х0,у0)
– некоторая точка плоскости, отличная
от О(0,0). Имеем: ψ(у)
= f(x0,y)=
.
Найдем fу′(M0),
где М0(х0,у0)
– некоторая точка плоскости, отличная
от О(0,0). Имеем: ψ(у)
= f(x0,y)=![]()
fу′(M0)
![]() ψ′(у0)
=
ψ′(у0)
=
Очевидно, частная производная функции f по у обладает свойствами, аналогичными свойствам 1),2) и 3) частной производной по х. Геометрии- ческий смысл числа fу′(M0) выясняется так же, как это было сделано выше для fх′(M0): пусть Г есть линия пересечения графика G : z =f(x,y) c плоско- стью х =х0 ; fу′(х0,у0) есть тангенс угла между осью ординат и касательной к Г , проведенной в точке N0(x0,y0,z0), где z0=f(x0,y0).
3.2 Частные производные функции n переменных
Пусть функция
f(х),
х = (х1,х2,…,хn)
определена в окрестности U![]() точки
х0
= (
точки
х0
= (![]() ).
Выбрав одно из чисел 1,2,…,n
,обозначим его через i и
положим φi(t)
= f (xt)
, где xt
=
).
Выбрав одно из чисел 1,2,…,n
,обозначим его через i и
положим φi(t)
= f (xt)
, где xt
=
![]() -
точка, координаты которой совпадают с
координатами х0,
за исключением i-той
координаты, равной t. Так
как f
определена в окрестности точки х0,
функция φi
определена для t,
близких к числу xi0
, т.е. в окрестности
Ux
-
точка, координаты которой совпадают с
координатами х0,
за исключением i-той
координаты, равной t. Так
как f
определена в окрестности точки х0,
функция φi
определена для t,
близких к числу xi0
, т.е. в окрестности
Ux![]() .
.
Определение 2. Если существует производная φ′i(xi0) , то это число называют частной производной от функции f по аргументу xi в точке х0 .
Обозначают
частную производную, введенную
определением 2 символами f ′х![]() (
х0) и
(
х0) и
![]() .
Таким образом,
.
Таким образом,
f ′х![]() (
х0)
(
х0)
![]() φ′i(xi0)=
φ′i(xi0)=![]() .
.
Обозначим : h= t - xi0. Тогда t = xi0+ h ; h →0 при t → xi0. Значит,
f ′х![]() (
х0) =
(
х0) =![]() =
=
![]()
Свойства f
′х![]() (
х0) вытекают из свойств
производной φ′i(xi0)
– они аналогичны утверждениям 1), 2)
и 3) ,п.3.1.
(
х0) вытекают из свойств
производной φ′i(xi0)
– они аналогичны утверждениям 1), 2)
и 3) ,п.3.1.
Пусть функция
f(x1,x2,…,xn)
определена на некотором открытом
множестве Х, Х![]() ,
и пусть в каждой точке х этого
множества существует частная производная
f ′х
,
и пусть в каждой точке х этого
множества существует частная производная
f ′х![]() (
х). Зададим на Х функцию g
i ,
сопоставив каждому х
(
х). Зададим на Х функцию g
i ,
сопоставив каждому х![]() число f ′х
число f ′х![]() (
х):
(
х):
![]() х
х![]() g (х) = f
′х
g (х) = f
′х![]() (
х). Функцию g
i называют
частной произ- водной от функции f
по аргументу х
(
х). Функцию g
i называют
частной произ- водной от функции f
по аргументу х![]() и обозначают символами f ′х
и обозначают символами f ′х![]() ,
f ′х
,
f ′х![]() (
х),
(
х),
![]() .
.
Пример 3.
![]() В примерах 1 и 2 были найдены частные
производные этой функции в произвольной
точке М0(х0,у0)
, отличной от О(0,0):
В примерах 1 и 2 были найдены частные
производные этой функции в произвольной
точке М0(х0,у0)
, отличной от О(0,0):
 ,
,![]() fу′(M0)=
fу′(M0)=
 Здесь х0 и у0
– координаты произвольной точки
плоскости. Заменив обозначения (х0,у0)
на (х,у), получим выражения, задающие
функции f ′х и f ′у
на проколотой плоскости :
Здесь х0 и у0
– координаты произвольной точки
плоскости. Заменив обозначения (х0,у0)
на (х,у), получим выражения, задающие
функции f ′х и f ′у
на проколотой плоскости :
![]() , fу′(х,у)=
, fу′(х,у)=
![]()
-
Функции, дифференцируемые в точке
Пусть функция
α определена в некоторой
проколотой окрестности точки 0(0,0,…,0)
и пусть
![]()
![]() .
Будем говорить в этом случае, что функция
α есть ″о - малое″ от
||x|| и записывать
при этом α(х) =
о(||x||).
.
Будем говорить в этом случае, что функция
α есть ″о - малое″ от
||x|| и записывать
при этом α(х) =
о(||x||).
Определение
3. Функцию f называют
дифференцируемой в точке х0
, х0![]() ,
если она определена в некоторой
окрестности этой точки , а для ее
приращения
,
если она определена в некоторой
окрестности этой точки , а для ее
приращения
![]() h)
, h = (
h1,h2,…,hn),
справедлива асимптотическая формула
h)
, h = (
h1,h2,…,hn),
справедлива асимптотическая формула
![]() (h)
= (А,h) +
α(h),
(1) где A
=( A1,A2,…,An)
– некоторый вектор, (А,h)
= А1h1+A2h2+…+Anhn
– скаляр- ное произведение
векторов, а α(h)
= о(||h ||).
(h)
= (А,h) +
α(h),
(1) где A
=( A1,A2,…,An)
– некоторый вектор, (А,h)
= А1h1+A2h2+…+Anhn
– скаляр- ное произведение
векторов, а α(h)
= о(||h ||).
Формула (1) эквивалентна каждой из следующих двух формул:
![]() (h)
= А1h1+A2h2+…+Anhn
+||h || ε(h),
(2) где ε(h)→
0 при h→ 0
и ε(0) = 0;
(h)
= А1h1+A2h2+…+Anhn
+||h || ε(h),
(2) где ε(h)→
0 при h→ 0
и ε(0) = 0;
![]() (h)
= А1h1+A2h2+…+Anhn
+h1 ε1(h)
+ h2
ε2(h)
+…+ hn
εn(h)
, (3) где при h→
0 εi
(h) →
0 , i = 1,2,…,n.
(h)
= А1h1+A2h2+…+Anhn
+h1 ε1(h)
+ h2
ε2(h)
+…+ hn
εn(h)
, (3) где при h→
0 εi
(h) →
0 , i = 1,2,…,n.
► Покажем, что из формулы (1) вытекает (2), из (2) вытекает (3), а из (3) следует (1) – тем самым будет доказана эквивалентность этих формул.
(1)![]() (2).
В некоторой окрестности U0
точки 0 зададим функцию
ε(h):
(2).
В некоторой окрестности U0
точки 0 зададим функцию
ε(h):
ε(h)=
![]()
При h
≠ 0 отсюда имеем:
![]() (h)
= (А,h)
+||h || ε(h),
причем ε(h)→
0 при h→ 0
и ε(0) = 0.
(h)
= (А,h)
+||h || ε(h),
причем ε(h)→
0 при h→ 0
и ε(0) = 0.
(2)![]() (3).
Имеем:
(3).
Имеем:
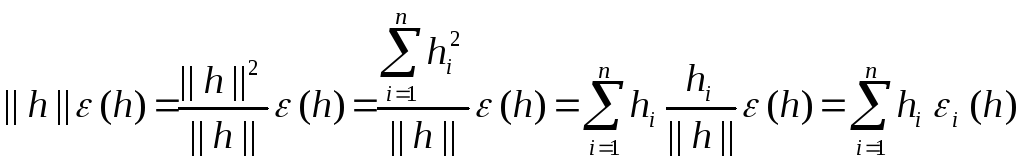 ,
,
где
![]() ,
i = 1,2,…,n.
Заметим:
,
i = 1,2,…,n.
Заметим:
![]() при h→ 0 ,
при h→ 0 ,
т.е. при h→
0 εi
(h) →
0 , i = 1,2,…,n.
Таким образом, заменив в (2) слагаемое
||h || ε(h)
на
![]() (h),
где εi
(h) введены
указанным выше способом, получим формулу
(3).
(h),
где εi
(h) введены
указанным выше способом, получим формулу
(3).
(3)![]() (1).
Обозначим: α(h)
=
(1).
Обозначим: α(h)
=
![]() (h).
Имеем:
(h).
Имеем:
![]() ,
,
и так как при
h→ 0 εi
(h) →
0 , i = 1,2,…,n,
то
![]() при h→ 0 ,
т.е. α(h)
= о(||h ||). Следовательно,
из (3) вытекает (1). ◄
при h→ 0 ,
т.е. α(h)
= о(||h ||). Следовательно,
из (3) вытекает (1). ◄
Теорема 1.
(Необходимые условия дифференцируемости)
Пусть функ- ция f дифференцируема
в точке х0. х0![]() .
Тогда 1) f непрерывна в точке
х0 и 2) в точке х0
существуют частные производные f
по каждому из ее аргументов.
.
Тогда 1) f непрерывна в точке
х0 и 2) в точке х0
существуют частные производные f
по каждому из ее аргументов.
►Из (1) легко
видеть, что
![]() (h)
→ 0 при h→ 0;
в силу теоремы о приращении непрерывной
функции ( п. 2.3) f непрерывна в точке
х0 .
(h)
→ 0 при h→ 0;
в силу теоремы о приращении непрерывной
функции ( п. 2.3) f непрерывна в точке
х0 .
2) Пусть i
– одно из чисел 1,2,…,n, а
h вектор,
все координаты которого равны нулю, за
исключением его i- той
координаты hi
, равной h≠ 0
: h = (
0,…,0,h,0,…,0). Так
как для такого вектора ||h||
= |h| , то, подставив
его в (1), получим:
![]() (h)
= Аih
+ α(|h|)
. Отсюда:
(h)
= Аih
+ α(|h|)
. Отсюда:
![]() так как α(h)
= о(||h ||). Таким
образом, частная производная f ′х
так как α(h)
= о(||h ||). Таким
образом, частная производная f ′х![]() (
х0) существует и
равна Аi
. ◄
(
х0) существует и
равна Аi
. ◄
Следствие.
Вектор А =( A1,A2,…,An)
в формулах (1), (2) и (3) определяется
единственным образом : А = (
![]() ) , так что, например, формулу (1) можно
записать так :
) , так что, например, формулу (1) можно
записать так :
![]() (h)
=
(h)
=
![]() о(||h ||).
о(||h ||).
Формулы (1), (2) и
(3) часто записывают в более компактном
виде с помощью символического вектора
(
![]() ), который называют оператором Гамильтона
и обозначают символом
), который называют оператором Гамильтона
и обозначают символом
![]() - ″набла″. Вектор А =
(
- ″набла″. Вектор А =
(
![]() ) представляют как произведение
символического вектора
) представляют как произведение
символического вектора
![]() на число f(х0);
тогда сумма
на число f(х0);
тогда сумма
![]() есть
скалярное произве-дение векторов
есть
скалярное произве-дение векторов
![]() f(х0)
и h :
f(х0)
и h :
![]() =
(
=
(![]() f(х0),
h). Теперь
формулу (2) , например, можно записать
так:
f(х0),
h). Теперь
формулу (2) , например, можно записать
так:
![]() (h)
= (
(h)
= (![]() f(х0),
h) + ||h
|| ε(h)
. (4)
f(х0),
h) + ||h
|| ε(h)
. (4)
Теорема 2.
(Достаточные условия дифференцируемости)
Пусть фун- кция f
(х1,х2, …,хn)
определена в некоторой окрестности
точки х0 , х0![]() ,
и имеет во всех точках этой окрестности
частные производные по каждому своему
аргументу. Если f
и ее частные производные f ′х
,
и имеет во всех точках этой окрестности
частные производные по каждому своему
аргументу. Если f
и ее частные производные f ′х![]() , i = 1,2,…,n
непрерывны в точке х0
, то функция f
дифференцируема в х0
.
, i = 1,2,…,n
непрерывны в точке х0
, то функция f
дифференцируема в х0
.
Мы приведем доказательство для случая n = 2; в общем случае оно про- водится по той же схеме, но становится весьма громоздким.
► Пусть функция
f (х,у) и ее частные
производные f ′х (х,у)
и fу′(х,у) оп-
ределены в некоторой ε – окрестности
U![]() (
ε) точки М0(х0,у0)
и непрерывны в этой точке. Нужно
установить дифференцируемость f
в точке М0 , для чего достаточно
доказать формулу (3), которую здесь можно
записать так:
(
ε) точки М0(х0,у0)
и непрерывны в этой точке. Нужно
установить дифференцируемость f
в точке М0 , для чего достаточно
доказать формулу (3), которую здесь можно
записать так:
![]() (h1,h2)
= fх′(M0)
h1 +
fу′(M0)
h2 + h1
ε1(h1,
h2) + h2
ε2
(h1, h2),
(5) где ε1(h1,
h2) и
ε2 (h1,
h2)
стремятся к нулю при h1
→0, h2→0.
(h1,h2)
= fх′(M0)
h1 +
fу′(M0)
h2 + h1
ε1(h1,
h2) + h2
ε2
(h1, h2),
(5) где ε1(h1,
h2) и
ε2 (h1,
h2)
стремятся к нулю при h1
→0, h2→0.
Пусть h1
и h2
выбраны так, что точка P
(х0+ h1
, у0+ h2
) содержится в окрестности U![]() (
ε). Тогда справедливы равенства
(
ε). Тогда справедливы равенства
![]() (h1,h2)
= f (х0+
h1 , у0+
h2 ) -
f (х0 ,
у0 ) =
(h1,h2)
= f (х0+
h1 , у0+
h2 ) -
f (х0 ,
у0 ) =
= f (х0+ h1 , у0+ h2 ) - f (х0 , у0+ h2 ) + f (х0 , у0+ h2 ) - f (х0 , у0 ). (6)
На сегменте
L1, ограниченном
точками х0 и х0+
h1,
определим функцию φ
равенством:
![]() L1 φ
(х) = f (х , у0+
h2 ).
Так как в U
L1 φ
(х) = f (х , у0+
h2 ).
Так как в U![]() (
ε) существует производная f ′х
,то в каждой точке сегмента L1
существует производная φ′(х)
= f ′х(х , у0+
h2 ).
Значит, функция φ
удовлетворяет на сег-
(
ε) существует производная f ′х
,то в каждой точке сегмента L1
существует производная φ′(х)
= f ′х(х , у0+
h2 ).
Значит, функция φ
удовлетворяет на сег-
менте L1 требованиям условия теоремы Лагранжа, и справедлива формула конечных приращений : φ (х0+ h1) - φ (х0) = φ′(х0+θ1 h1) h1. где θ1 – некоторое число , 0 < θ1 < 1. Отсюда, так как φ (х) = f (х , у0+ h2 ), получим:
f (х0+ h1 , у0+ h2 ) - f (х0 , у0+ h2 ) = f ′х( х0+θ1 h1, у0+ h2 ) h1
Аналогично, рассмотрев функцию ψ(у) = f (х0 , у ) на сементе L2, ограни- ченном точками у0 и у0+ h2, получим равенство
f (х0 , у0+ h2 ) - f (х0 , у02 ) = f ′у( х0 , у0+ θ2 h2 ) h2.
Таким образом, из (6) теперь следует:
![]() (h1,h2)
= f ′х( х0+θ1
h1, у0+
h2 )
h1 + f ′у(
х0 , у0+ θ2
h2 )
h2.
(7)
(h1,h2)
= f ′х( х0+θ1
h1, у0+
h2 )
h1 + f ′у(
х0 , у0+ θ2
h2 )
h2.
(7)
Обозначим : ε1(h1, h2) = f ′х( х0+θ1 h1, у0+ h2 ) - f ′х( х0 , у0 ) ,
ε2 (h1, h2) = f ′у( х0 , у0+ θ2 h2 ) - f ′у( х0 , у0 ).
Тогда f ′х( х0+θ1 h1, у0+ h2 ) = f ′х( х0 , у0 ) + ε1(h1, h2), (8)
f ′у( х0 , у0+ θ2 h2 ) = f ′у( х0 , у0 ) + ε2 (h1, h2), (9)
причем из
непрерывности функций f ′х и
f ′у следует, что ε1(h1,
h2) и
ε2
(h1, h2)
стремятся к нулю при h1
→0, h2→0.
После подстановки (8) и (9) в (7) получим
для
![]() (h1,h2)
представление (5) . ◄
(h1,h2)
представление (5) . ◄
Пусть m и n - некоторые натуральные числа.
Теорема 3.
(О дифференцируемости сложной
функции) Пусть функции φ1(t),
φ2(t),
…, φn(t)
, где t = ( t1,t2,
…,tm
), дифференцируемы в точке t0![]() ,
а функция f
(х1,х2, …,хn)
дифференцируема в точке х0
,
а функция f
(х1,х2, …,хn)
дифференцируема в точке х0![]() ,
х0 =(х10,х20,
…,хn0),
где хi0
= φi
(t0),
i = 1,2,…,n.
Тогда сложнaя функция
F(t)
= f(φ1(t),
φ2(t),…,φn(t))
дифференцируема в точке t0
, причем
,
х0 =(х10,х20,
…,хn0),
где хi0
= φi
(t0),
i = 1,2,…,n.
Тогда сложнaя функция
F(t)
= f(φ1(t),
φ2(t),…,φn(t))
дифференцируема в точке t0
, причем
F′![]() (t0)=
(t0)=
![]() , k = 1,2,…,m
. (10)
, k = 1,2,…,m
. (10)
► Согласно
определению 3 нужно показать, что 1) F
определена в некоторой окрестности
точки t0
и что 2) для приращения
![]() (τ)
= F(t0+
τ) - F(t0)
, τ
= (τ1,
τ2, …,
τm)
, справедливо представление
(τ)
= F(t0+
τ) - F(t0)
, τ
= (τ1,
τ2, …,
τm)
, справедливо представление
![]() (τ)
=
(τ)
=
![]() +
α (τ)
, где Ak
, k = 1,2,…,m
- некоторые числа, а α
(τ) = о (||τ||)
.
+
α (τ)
, где Ak
, k = 1,2,…,m
- некоторые числа, а α
(τ) = о (||τ||)
.
1) Функции f и φi , i = 1,2,…,n – дифференцируемые, а потому и непре- рывные функции. Значит, требования условия теоремы 4, п. 2.3, выполнены, и в силу утверждения 1) этой теоремы найдется ε > 0 такое,что F определена в ε - окрестности точки t0 .
2) Пусть вектор
τ = (τ1,
τ2, …,
τm)
удовлетворяет требованию ||τ||
< ε . Обозначим: hi=
φi(t0+
τ)- φi
(t0)=
![]() (τ)
, i = 1,2,…,n .
Отсюда, так как φi
(t0)
= хi0
, получим: φi(t0+
τ) = хi0+
hi
, i = 1,2,…,n
. Следовательно,
(τ)
, i = 1,2,…,n .
Отсюда, так как φi
(t0)
= хi0
, получим: φi(t0+
τ) = хi0+
hi
, i = 1,2,…,n
. Следовательно,
![]() (τ)
= F(t0+
τ) - F(t0)
= f(φ1(t0+
τ ), φ2(t0+
τ), …, φn(t0+
τ)) - f(φ1(t0),
φ2(t0),
…, φn(t0))
= f(х10+
h1,
х20+
h2 ,…,
хn0+
hn)
- f(х10,
х20 ,…,
хn0)
= f
(х0+
h )
- f (х0
)=
(τ)
= F(t0+
τ) - F(t0)
= f(φ1(t0+
τ ), φ2(t0+
τ), …, φn(t0+
τ)) - f(φ1(t0),
φ2(t0),
…, φn(t0))
= f(х10+
h1,
х20+
h2 ,…,
хn0+
hn)
- f(х10,
х20 ,…,
хn0)
= f
(х0+
h )
- f (х0
)=![]() (h)
,
(h)
,
где h = (h1,h2, …,hn) . Так как f дифференцируема в точке х0 , то
![]() (τ)
=
(τ)
=
![]() (h)
=
(h)
=
![]() f ′х
f ′х![]() (
х0)
hi
+
||h
|| ε(h)
, (11) где ε(h)→
0 при h →
0.
Функции φi
дифференцируемы в точке t0
, поэтому при каждом i
= 1,2,…,n hi=
(
х0)
hi
+
||h
|| ε(h)
, (11) где ε(h)→
0 при h →
0.
Функции φi
дифференцируемы в точке t0
, поэтому при каждом i
= 1,2,…,n hi=
![]() (τ)
=
(τ)
=
![]() + || τ|| εi(τ)
, где εi(τ)
→ 0 при τ →
0 . Подставим эти
выражения для hi
в (11) :
+ || τ|| εi(τ)
, где εi(τ)
→ 0 при τ →
0 . Подставим эти
выражения для hi
в (11) :
![]() (τ)
=
(τ)
=![]() f ′х
f ′х![]() (
х0)
(
х0)
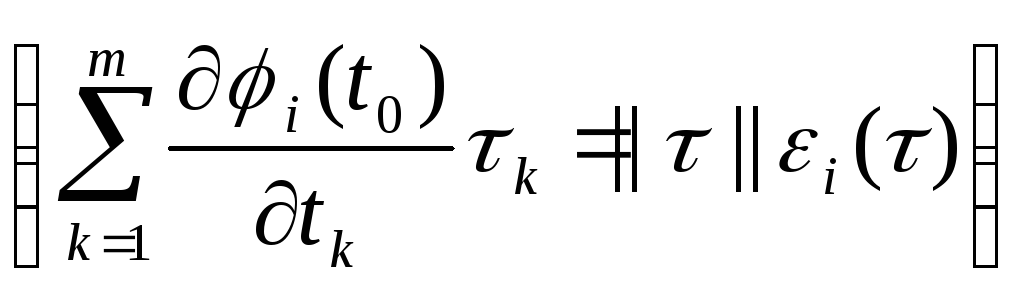 +||h
|| ε(h)
=
+||h
|| ε(h)
=
=![]() f ′х
f ′х![]() (
х0)
(
х0)
![]() +
|| τ||
+
|| τ||![]() f ′х
f ′х![]() (
х0)
εi(τ)
+||h
|| ε(h)
. Меняя порядок
суммирования в двойной сумме, получим
:
(
х0)
εi(τ)
+||h
|| ε(h)
. Меняя порядок
суммирования в двойной сумме, получим
:
![]() (τ)
=
(τ)
=
![]() +
α (τ)
, (12)
+
α (τ)
, (12)
где Ak
=
![]() f ′х
f ′х![]() (
х0)
(
х0)
![]() ,
k =1,2,…,m
,
,
k =1,2,…,m
,
α
(τ) = || τ||![]() f ′х
f ′х![]() (
х0) εi(τ)
+||h || ε(h)
.
(
х0) εi(τ)
+||h || ε(h)
.
Покажем, что α
(τ) =о (||τ||)
, т.е.
![]() Имеем при τ ,
удовлетво- ряющих неравенствам 0
< || τ|| <
ε :
Имеем при τ ,
удовлетво- ряющих неравенствам 0
< || τ|| <
ε :
![]() =
β(τ)
+ γ (τ)
, где β(τ)
=
=
β(τ)
+ γ (τ)
, где β(τ)
=
![]() f ′х
f ′х![]() (
х0) εi(τ)
, γ (τ)
=
(
х0) εi(τ)
, γ (τ)
=
![]() ε(h)
. Так как εi(τ)
→ 0 при τ →
0 , i = 1,2,…,n
, то β(τ)
→ 0 при τ →
0. Покажем, что и γ
(τ) → 0 при τ
→ 0.
ε(h)
. Так как εi(τ)
→ 0 при τ →
0 , i = 1,2,…,n
, то β(τ)
→ 0 при τ →
0. Покажем, что и γ
(τ) → 0 при τ
→ 0.
Так как hi=
![]() (τ)
, а φi
непрерывна в точке t0
, то по теореме о прира- щении
непрерывной функции hi
→ 0 при τ
→ 0. Значит, h
= (h1,h2,
…,hn)
→ 0 при τ
→ 0 . Но ε(h)→
0 при h →
0, следовательно, ε(h)→
0 при τ → 0.
(τ)
, а φi
непрерывна в точке t0
, то по теореме о прира- щении
непрерывной функции hi
→ 0 при τ
→ 0. Значит, h
= (h1,h2,
…,hn)
→ 0 при τ
→ 0 . Но ε(h)→
0 при h →
0, следовательно, ε(h)→
0 при τ → 0.
Воспользовавшись
формулой (4), можем записать: hi
=
![]() (τ)
= (
(τ)
= (![]() φi(t0),
τ ) +
|| τ
|| εi(τ
) . Отсюда: | hi|
≤ | (
φi(t0),
τ ) +
|| τ
|| εi(τ
) . Отсюда: | hi|
≤ | (![]() φi(t0),
τ ) |
+ || τ || |
εi(τ
)| . В силу неравенства Коши-
Буняковского ( п. 1.1 ) | (
φi(t0),
τ ) |
+ || τ || |
εi(τ
)| . В силу неравенства Коши-
Буняковского ( п. 1.1 ) | (![]() φi(t0),
τ ) |
≤ ||
φi(t0),
τ ) |
≤ ||![]() φi(t0)||
|| τ || .
Обозначим через
М наибольшее
из чисел
||
φi(t0)||
|| τ || .
Обозначим через
М наибольшее
из чисел
||![]() φi(t0)||
, i =1,2,…,n. Так как
εi(τ)
→ 0 при τ →
0 ,
i = 1,2,…,n , найдется δ , 0 < δ < ε , такое,что
при всех τ , 0
< || τ||
≤ δ и всех i = 1,2,…,n справедливо |
εi(τ
)| ≤ М. Значит, при
всех τ , 0
< || τ||
≤ δ и всех i = 1,2,…,n
φi(t0)||
, i =1,2,…,n. Так как
εi(τ)
→ 0 при τ →
0 ,
i = 1,2,…,n , найдется δ , 0 < δ < ε , такое,что
при всех τ , 0
< || τ||
≤ δ и всех i = 1,2,…,n справедливо |
εi(τ
)| ≤ М. Значит, при
всех τ , 0
< || τ||
≤ δ и всех i = 1,2,…,n
|
hi|
≤ ||![]() φi(t0)||
|| τ
|| + || τ
|| | εi(τ
)| ≤ М ||
τ || + ||
τ || М = 2М ||
τ || .
φi(t0)||
|| τ
|| + || τ
|| | εi(τ
)| ≤ М ||
τ || + ||
τ || М = 2М ||
τ || .
Теперь при 0 < || τ|| ≤ δ имеем:
 Следовательно, дробь
Следовательно, дробь
![]() есть
функция от τ,
ограниченная в проколотой δ-
окрестности точки 0; таким
образом, γ (τ)
представляет собой произведение
ограниченной функции
есть
функция от τ,
ограниченная в проколотой δ-
окрестности точки 0; таким
образом, γ (τ)
представляет собой произведение
ограниченной функции
![]() на
бесконечно малую при τ
→ 0 функцию ε(h)
, поэтому γ (τ)
→ 0 при τ →
0.
на
бесконечно малую при τ
→ 0 функцию ε(h)
, поэтому γ (τ)
→ 0 при τ →
0.
Итак, при τ → 0 β(τ) → 0 и γ (τ) → 0 ; значит, α (τ) =о (||τ||). Отсюда и из (12) вытекает и дифференцируемость F в точке t0 , и выражения для ее частных производных:
F′![]() (t0)=Аk
=
(t0)=Аk
=
![]() , k = 1,2,…,m
. ◄
, k = 1,2,…,m
. ◄
Отметим частные случаи формул (10)
Пусть φi
, i = 1,2,…,n –
функции одной переменной t,
дифференцируе -мые в точке t0
, а функция f (х1,х2,
…,хn)
дифференцируема в точке х0![]() ,
х0 =(х10,х20,
…,хn0),
где хi0
= φi
(t0),
i = 1,2,…,n.
Тогда сложнaя функция
F(t)
= f(φ1(t),
φ2(t),
…, φn(t))
дифференцируема в точке t0
, причем
,
х0 =(х10,х20,
…,хn0),
где хi0
= φi
(t0),
i = 1,2,…,n.
Тогда сложнaя функция
F(t)
= f(φ1(t),
φ2(t),
…, φn(t))
дифференцируема в точке t0
, причем
![]()
Пусть функции φ (u,v) и ψ(u,v) дифференцируемы в точке N0 (u0,v0) , а f (x,y) дифференцируема в точке M0(x0,y0) , где x0 = φ (u0,v0) , y0 = ψ(u0,v0) . Тогда функция F( u,v) = f( φ (u,v), ψ(u,v)) дифференцируема в точке N0 , причем
![]()
![]()
Замечание.
Пусть обозначения φi
, i = 1,2,…,n ,
f , t
, x,
t0 ,
x0
имеют тот же смысл, что в тексте
теоремы 3, и пусть переменная u
есть сложная функция переменных
t1,t2,
…,tm
: u = f(φ1(t),
φ2(t),
…, φn(t))
= F (t1,t2,
…,tm)
. Условимся в следующих обозначениях :
через u′![]() или
или
![]() обозначаем частные производные функции
f по ее аргументам
х1,х2, …,хn
; через u′
обозначаем частные производные функции
f по ее аргументам
х1,х2, …,хn
; через u′![]() или
или
![]() обознаёчаем частные производные функции
F (t1,t2,
…,tm)
, через
обознаёчаем частные производные функции
F (t1,t2,
…,tm)
, через
![]() обозначаем частные призводные функции
φi(t1,t2,
…,tm)
. Тогда формулы (10) можно записать в
следующем виде : u′
обозначаем частные призводные функции
φi(t1,t2,
…,tm)
. Тогда формулы (10) можно записать в
следующем виде : u′![]() =
=
![]() , k = 1,2,…,m
.
, k = 1,2,…,m
.
Определение
4. Будем говорить, что функция f
(х1,х2, …,хn)
дифферен- цируема на открытом множестве
Х![]() ,
если она дифференцируема в каждой точке
этого множества.
,
если она дифференцируема в каждой точке
этого множества.
Определение
5. Будем говорить, что функция f
(х1,х2, …,хn)
непрерывно дифференцируема на открытом
множестве Х![]() ,
если она дифференцируе- ма на этом
множестве и ее частные производные по
всем ее аргументам непрерывны на Х.
,
если она дифференцируе- ма на этом
множестве и ее частные производные по
всем ее аргументам непрерывны на Х.
3.4 Дифференциал функции в точке. Инвариантность формы
дифференциала .
Пусть функция f (x) , x = (x1,x2,…,xn) , дифференцируема в точке х0 . Тог- да для ее приращения справедливо представление (h = (h1,h2,…,hn) ) :
![]() f(h)
=
f(h)
=
![]() + o(||h||).
+ o(||h||).
Выражение
![]() в этом представлении называют
дифференциа -лом функции f
в точке х0 и
обозначают символами
в этом представлении называют
дифференциа -лом функции f
в точке х0 и
обозначают символами
![]() или
или
![]() h)
:
h)
:
![]() h)
h)
![]() .
.
Пример 1.
![]() Пусть М0 (х0 ,у0)
– некоторая точка, отличная от О(0,0).
Имеем ( см.п. 3.2) :
Пусть М0 (х0 ,у0)
– некоторая точка, отличная от О(0,0).
Имеем ( см.п. 3.2) :
 ,
,![]() fу′(M0)=
fу′(M0)=
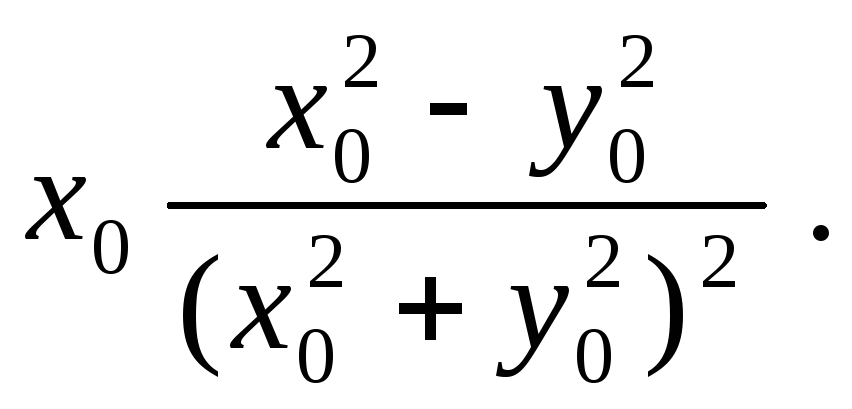 Значит,
Значит,
![]()

 .
В частности, при х0=1,
у0= 2
.
В частности, при х0=1,
у0= 2
![]()
![]() .
Если же х0= у0=1,
то
.
Если же х0= у0=1,
то
![]() fу′(M0)= 0 , и потому
fу′(M0)= 0 , и потому
![]() 0
при любых h1
и h2,
т.е.
0
при любых h1
и h2,
т.е.
![]() ≡
0.
≡
0.
Имеем :
![]() f(h)
= f(х0+h)
– f(x0)
, где x0
= (x10,x20,…,xn0)
, h =
(h1,h2,…,hn).
Обозначим : х = х0+h
, x =
(x1,x2,…,xn);
тогда h = х -
х0 , hi
= xi
– xi0
, i = 1,2, …,n.
Разность xi
– xi0
называют приращением аргумента
(независимой пере- менной) xi
и обозначают ее через Δ
xi
; эту же разность называют также
диф- ференциалом аргумента (независимой
переменной) xi
и обозначают ее в та- ком случае
через d xi
. Таким образом, выражение для
f(h)
= f(х0+h)
– f(x0)
, где x0
= (x10,x20,…,xn0)
, h =
(h1,h2,…,hn).
Обозначим : х = х0+h
, x =
(x1,x2,…,xn);
тогда h = х -
х0 , hi
= xi
– xi0
, i = 1,2, …,n.
Разность xi
– xi0
называют приращением аргумента
(независимой пере- менной) xi
и обозначают ее через Δ
xi
; эту же разность называют также
диф- ференциалом аргумента (независимой
переменной) xi
и обозначают ее в та- ком случае
через d xi
. Таким образом, выражение для
![]() h)
можно запи- сать в следующей форме :
h)
можно запи- сать в следующей форме :
![]() h)
=
h)
=
![]() (13)
(13)
Из свойств частных производных нетрудно вывести следующие правила вычисления дифференциалов в точке х0 : пусть функции f и g дифференцируемы в точке х0 ; тогда
1. если в окрестности точки х0 f (х) ≡ Соnst , то df ≡ 0 ;
-
d(f+g) = df + dg;
-
d(f g) = g df +f dg; в частности, если f (х) ≡ С, то d(Сg) = С dg;
-
если g(x0) ≠ 0, то
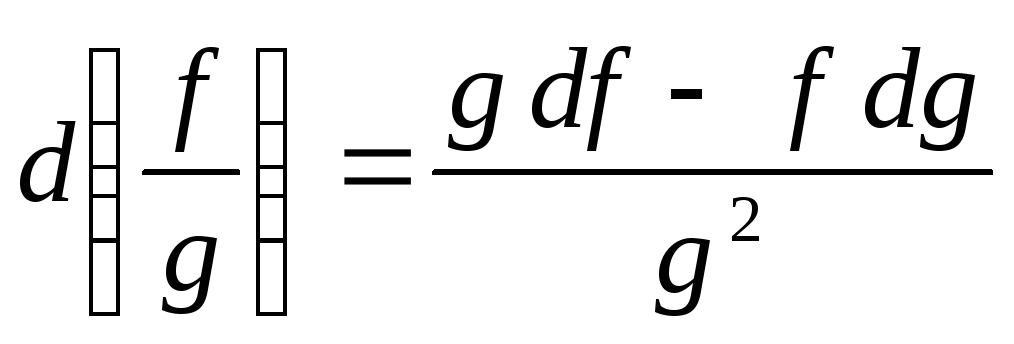 .
.
Выведем формулу
для дифференциала сложной функции.
Пусть F(t)=
=f(φ1(t),
φ2(t),
…, φn(t))
, где функции φi
, i = 1,2,…,n,
дифференцируемы в точке t0![]() ,
а функция f дифференцируема
в точке х0
,
а функция f дифференцируема
в точке х0![]() ,
х0 =(х10,х20,
…,хn0),
где хi0
= φi
(t0),
i = 1,2,…,n. По
теореме 3 , п 3.3., функция F(t)
=F ( t1,t2,
…,tm
) дифференцируема в точке t0
. Запишем ее
дифференциал :
,
х0 =(х10,х20,
…,хn0),
где хi0
= φi
(t0),
i = 1,2,…,n. По
теореме 3 , п 3.3., функция F(t)
=F ( t1,t2,
…,tm
) дифференцируема в точке t0
. Запишем ее
дифференциал :
![]() .
Воспользуемся формулами (10) :
.
Воспользуемся формулами (10) :
 . Отсюда, так как
. Отсюда, так как
![]() ,
получим:
,
получим:
![]() (14)
(14)
Опишем теперь свойство дифференциала, которое называют ивариант- ностью (неизменностью) его формы. Пусть переменная u является функцией от n переменных x1,x2,…,xn, дифференцируемой в точке х0 : u = f (х1,х2, …,хn) . Дифференциал du выражается формулой (13), которую, используя обозначе- ния, принятые в замечании п. 3.3, можно записать так:
du =![]() .
(15)
.
(15)
Пусть теперь
каждая из переменных x1,x2,…,xn
представляет собой дифференцируемую
функцию переменных t1,t2,
…,tm
: xi
= φi(t1,t2,
…,tm),
i = 1,2, …,n.
Тогда переменная u
является сложной функцией от t1,t2,
…,tm,
а ее дифференциал в обозначениях
замечания п.3.3 будет записан в виде du=
![]()
![]() ;
его же в виду формулы (14) можно записать
и так: du =
;
его же в виду формулы (14) можно записать
и так: du =![]() , что совпадает с (15). Таким образом, если
переменная u
является функцией от n
переменных x1,x2,…,xn
, то ее дифферен- циал du
записывается формулой (15) как в случае,
когда x1,x2,…,xn
являются независимыми переменными,
так и тогда, когда они в свою очередь
предс- тавляют собой функции от некоторых
переменных t1,t2,
…,tm
- в этом и состо- ит инвариантность
формы du . Однако,
следует помнить о существенном раз-
личии между этими двумя случаями в
содержании формулы (15). Если пере- менные
x1,x2,…,xn
независимы, то их дифференциалы –
это их приращения, следовательно,
значения dxi
, i= 1,2, …,n
в (15) можно назначать произвольно. Во
втором случае dxi
есть дифференциал функции
φi(t1,t2,…,tm),
т.е., величи- на, зависящая от значений
дифференциалов dtk
, k= 1,2, …,k.
, что совпадает с (15). Таким образом, если
переменная u
является функцией от n
переменных x1,x2,…,xn
, то ее дифферен- циал du
записывается формулой (15) как в случае,
когда x1,x2,…,xn
являются независимыми переменными,
так и тогда, когда они в свою очередь
предс- тавляют собой функции от некоторых
переменных t1,t2,
…,tm
- в этом и состо- ит инвариантность
формы du . Однако,
следует помнить о существенном раз-
личии между этими двумя случаями в
содержании формулы (15). Если пере- менные
x1,x2,…,xn
независимы, то их дифференциалы –
это их приращения, следовательно,
значения dxi
, i= 1,2, …,n
в (15) можно назначать произвольно. Во
втором случае dxi
есть дифференциал функции
φi(t1,t2,…,tm),
т.е., величи- на, зависящая от значений
дифференциалов dtk
, k= 1,2, …,k.
-
Касательная плоскость к графику функции двух переменных
Пусть функция
f(x,y)
определена в некоторой окрестности
U![]() точки М0(х0,у0)
, G – график функции,
т.е. поверхность с уравнением z
= f(x,y),
а N0 – точка
графика G, проекцией
которой на плоскость ХОY
является М0 , т.е. N0(х0,у0,
z0)
, где z0
= f(х0,у0).
Пусть П – плоскость, проходящая
через N0 и не
параллельная оси OZ.
Уравнение плоскости П запишем в
виде z = l
(x,y),
где l(x,y)
= z0 + A
(x – x0)
+ B (y
– y0) , A
и B – некоторые
числа.
точки М0(х0,у0)
, G – график функции,
т.е. поверхность с уравнением z
= f(x,y),
а N0 – точка
графика G, проекцией
которой на плоскость ХОY
является М0 , т.е. N0(х0,у0,
z0)
, где z0
= f(х0,у0).
Пусть П – плоскость, проходящая
через N0 и не
параллельная оси OZ.
Уравнение плоскости П запишем в
виде z = l
(x,y),
где l(x,y)
= z0 + A
(x – x0)
+ B (y
– y0) , A
и B – некоторые
числа.
Пусть М(х,у)
– некоторая точка, принадлежащая U![]() , а N и Р – точки , имеющие
одинаковые с М абсциссу и ординату,
причём N лежит на поверх-
ности G, а P
- на плоскости П : N
(x,y,zG
), P (x,y,zП),
где zG
=f(х,у) , zП
= l(х,у) (
рис. 4).
, а N и Р – точки , имеющие
одинаковые с М абсциссу и ординату,
причём N лежит на поверх-
ности G, а P
- на плоскости П : N
(x,y,zG
), P (x,y,zП),
где zG
=f(х,у) , zП
= l(х,у) (
рис. 4).
 Обозначим:
h1= x
- x0 , h2=
y – y0
, h =
=
Обозначим:
h1= x
- x0 , h2=
y – y0
, h =
=
![]() = (h1, h2).
Заметим : || h
|| есть рас- стояние между точками М0
и М , а zG
– zП –
расстояние между точками N
и Р, первая из которых лежит на графике
G, а вторая – на
плоскости П.
= (h1, h2).
Заметим : || h
|| есть рас- стояние между точками М0
и М , а zG
– zП –
расстояние между точками N
и Р, первая из которых лежит на графике
G, а вторая – на
плоскости П.
Определение 4. Плоскость П называют касательной плоскостью к по- верхности G в точке N0, если разность аппликат zG – zП точек N и P есть о(||h||):
 .
.
Теорема 4.
(О касательной плоскости) Пусть
функция f(x,y)
опреде- лена в некоторой окрестности
U![]() точки М0(х0,у0),
а G – график этой
функ- ции, т.е. поверхность, уравнение
которой z = f(x,y)
. Тогда:
точки М0(х0,у0),
а G – график этой
функ- ции, т.е. поверхность, уравнение
которой z = f(x,y)
. Тогда:
1) для того, чтобы существовала касательная плоскость к поверхности G в точке N0(x0,y0,z0 ), где z0 = f(х0,у0), необходимо и достаточно, чтобы f была дифференцируема в точке М0;
2) если функция f дифференцируема в точке М0 , то плоскость П, урав- нение уравнение которой
z = z0 + f′x(x0,y0) (x – x0) + f′y(x0,y0) (y – y0) , (16)
является касательной плоскостью к поверхности G а точке N0;
3) если касательная плоскость к поверхности G а точке N0 существует, то только одна.
► 1) Необходимость. Пусть f дифференцируема в точке М0 . Покажем, что тогда касательная плоскость существует, а именно, что плоскость П, за- данная уравнением (16), удовлетворяет определению 4. Действительно, f дифференцируема в точке М0 , поэтому
Δ![]() f (h1
,h2 ) =
f′x(x0,y0)
h1 +
f′y(x0,y0)
h2 +
o(||h||)
, т.е., так как
Δ
f (h1
,h2 ) =
f′x(x0,y0)
h1 +
f′y(x0,y0)
h2 +
o(||h||)
, т.е., так как
Δ![]() f (h1
,h2 )=
f(х,у) - f(х0,у0)
= zG
- z0 ,
f (h1
,h2 )=
f(х,у) - f(х0,у0)
= zG
- z0 ,
zG - z0 = f′x(x0,y0) h1 + f′y(x0,y0) h2 + o(||h||) .
Отсюда : zG - ( z0 + f′x(x0,y0) (x – x0) + f′y(x0,y0) (y – y0) ) = o(||h||). Выраже- ние в скобке есть правая часть уравнения (16). Обозначив её через zП , полу- чим: zG – zП = о(||h||). Значит, П – касательная плоскость.
Достаточность.
Пусть плоскость П, заданная
уравнением z = l
(x,y),
где l(x,y)
= z0 + A
(x – x0)
+ B (y
– y0) , A
и B – некоторые
числа, является ка- сательной плоскостью
к графику G в точке
N0 . Обозначим :
zG=
f(M)
, zП =
l(M)
, где М(х,у) – точка, принадлежащая
U![]() .
Тогда в силу определения 4 zG
– zП =
о(||h||) , где h
=
.
Тогда в силу определения 4 zG
– zП =
о(||h||) , где h
=
![]() = (h1, h2)
, h1= x
- x0, h2=
y – y0
. Заметим:
= (h1, h2)
, h1= x
- x0, h2=
y – y0
. Заметим:
zG
– zП =
f(M) -
l(M)= f
(x,y) - l(x,y) = f (x,y) – (z0
+ A (x – x0)
+ B (y – y0)
) Отсюда
: f (x,y)
– z0
= A (x –
x0)
+ B (y – y0)
+ о(||h||)
. Но
![]()
f
(x,y)
– z0=
f(х0+h,у0+h)
- f(х0,у0)
= Δ![]() f (h1
,h2 ).
Значит,
Δ
f (h1
,h2 ).
Значит,
Δ![]() f (h1
,h2 )= A
h1 + Bh2
+ о(||h||) , т.е., f
дифференцируема в точке М0 .Тем
самым достаточность доказана. Заметим,
что здесь А = f′x(x0,y0)
, В = f′y(x0,y0),
так что если z = z0
+ A (x
– x0) + B
(y – y0)
есть уравнение касатель- ной плоскости,
то A и B
определяются единственным образом:
А = f′x(x0,y0)
, В = f′y(x0,y0).
Следовательно,если П – касательная
плоскость к к графику G
в точке N0, то её
уравнение есть уравнение (16).
f (h1
,h2 )= A
h1 + Bh2
+ о(||h||) , т.е., f
дифференцируема в точке М0 .Тем
самым достаточность доказана. Заметим,
что здесь А = f′x(x0,y0)
, В = f′y(x0,y0),
так что если z = z0
+ A (x
– x0) + B
(y – y0)
есть уравнение касатель- ной плоскости,
то A и B
определяются единственным образом:
А = f′x(x0,y0)
, В = f′y(x0,y0).
Следовательно,если П – касательная
плоскость к к графику G
в точке N0, то её
уравнение есть уравнение (16).
-
Если f дифференцируема в точке М0 , то плоскость, заданная уравне- нием (16) есть касательная плоскость – это было установлено при доказатель- стве Необходимости.
-
При доказательстве Достаточности установлена единственность этой касательной плоскости. ◄
Пример. f
(x,y)
=
![]() .
Эта функция дифференцируема во всех
точках плоскости, ее график – параболоид
вращения z =
.
Эта функция дифференцируема во всех
точках плоскости, ее график – параболоид
вращения z =
![]() .
Следовательно, в каждой
точке параболоида существует касательная
плоскость. Запишем урав- нение
плоскости, касающейся параболоида в
точке Р0 (1,2,5). Имеем: f′x(x,y)
= 2х , f′x(x,y)
=2у . Подставив в уравнение (16) эти
производные, х0 = 1, у0
= 2 , z0 =
5 , получим: z = 5 + 2(х
– 1) + 4(у – 2) , т.е. 2х + 4у – z
– 5 = 0 .
.
Следовательно, в каждой
точке параболоида существует касательная
плоскость. Запишем урав- нение
плоскости, касающейся параболоида в
точке Р0 (1,2,5). Имеем: f′x(x,y)
= 2х , f′x(x,y)
=2у . Подставив в уравнение (16) эти
производные, х0 = 1, у0
= 2 , z0 =
5 , получим: z = 5 + 2(х
– 1) + 4(у – 2) , т.е. 2х + 4у – z
– 5 = 0 .
Замечание. Пусть f (x,y) дифференцируема в точке М0(х0,у0), G : z = =f (x,y) – график этой функции, N0 (х0,у0, z0) , z0 = f(х0,у0) , - точка, принадле- жащая G, П – плоскость, касающаяся G в точке N0 . Пусть, далее, Г – гладкая кривая, все точки которой принадлежат G , и которая проходит через N0 , а Δ – касательная прямая к Г в точке N0. Покажем, что касательная Δ лежит в ка- сательной плоскости П . Действительно, пусть

- уравнение Г, а t0
– точка на (α,β)
такая, что
![]() .
Так как все точки Г принадлежат
G, то функции
.
Так как все точки Г принадлежат
G, то функции
![]() удовлетворяют урав- нению z
= f (x,y)
на (α,β):
удовлетворяют урав- нению z
= f (x,y)
на (α,β):
![]() .
Продифференцировав это тождест- во и
подставив t = t0,
получим:
.
Продифференцировав это тождест- во и
подставив t = t0,
получим:
![]() ,
т.е.
,
т.е.
![]() .
Левая часть этого равенства представ-
ляет собой скалярное произведение
векторов
.
Левая часть этого равенства представ-
ляет собой скалярное произведение
векторов
![]() и
и
![]()
![]() ;
следовательно, угол между этими векторами
прямой. Напомним, что
;
следовательно, угол между этими векторами
прямой. Напомним, что
![]() есть нормальный вектор плоскости П
( см. уравнение (16)), а
есть нормальный вектор плоскости П
( см. уравнение (16)), а
![]() -
направляющий вектор касательной Δ.
Значит, касательная Δ
парал- лельна плоскости П , и так как
Δ проходит через точку
N0 , дежащую на П,
то Δ лежит на П.
-
направляющий вектор касательной Δ.
Значит, касательная Δ
парал- лельна плоскости П , и так как
Δ проходит через точку
N0 , дежащую на П,
то Δ лежит на П.
-
Частные производные высших порядков
Пусть
функция f(x,y)
дифференцируема на некотором открытом
мно- жестве
![]() .
Из теоремы о необходимых условиях
дифференцируемости вытекает, что на Х
определены
частные производные
.
Из теоремы о необходимых условиях
дифференцируемости вытекает, что на Х
определены
частные производные
![]() и
и
![]() .
Эти функции могут оказаться дифференцируемыми
на Х. В
этом случае на Х
оп- ределены
частные производные этих функций.
Частные производные от
.
Эти функции могут оказаться дифференцируемыми
на Х. В
этом случае на Х
оп- ределены
частные производные этих функций.
Частные производные от
![]() и
и
![]() называют частными производными второго
порядка от функ- ции f(x,y),
при этом
называют частными производными второго
порядка от функ- ции f(x,y),
при этом
![]() и
и
![]() называют частными производными пер-
вого порядка от функции f(x,y).
Приняты следующие обозначения:
называют частными производными пер-
вого порядка от функции f(x,y).
Приняты следующие обозначения:
![]() -
частная производная второго порядка
от функции f(x,y)
по х дважды
(частная производная от
-
частная производная второго порядка
от функции f(x,y)
по х дважды
(частная производная от
![]() по х);
по х);
![]() -
частная производная второго порядка
от функции f(x,y)
по ху (
частная производная от
-
частная производная второго порядка
от функции f(x,y)
по ху (
частная производная от
![]() по у);
по у);
![]() -
частная производная второго порядка
от функции f(x,y)
по ух (
частная производная от
-
частная производная второго порядка
от функции f(x,y)
по ух (
частная производная от
![]() по х);
по х);
![]() -
частная производная второго порядка
от функции f(x,y)
по у дважды
( частная производная от
-
частная производная второго порядка
от функции f(x,y)
по у дважды
( частная производная от
![]() по у).
по у).
Если
частные производные второго порядка
дифференцируемые функ- ции,то их частные
производные называют частными производными
третьего порядка от функции f(x,y).
Вообще, частными производными порядка
![]()
![]() от
функции f(x,y)
называют частные производные от её
частных произ- водных порядка
от
функции f(x,y)
называют частные производные от её
частных произ- водных порядка
![]() .
.
Производные
![]() и
и![]() называют
смешанными частными производ- ными
второго порядка функции f(x,y).
Если функция f(x,y)
удовлетворяет условиям, указанным в
приведённой ниже теореме, справедливо
равенство
называют
смешанными частными производ- ными
второго порядка функции f(x,y).
Если функция f(x,y)
удовлетворяет условиям, указанным в
приведённой ниже теореме, справедливо
равенство
![]() =
=![]() .
.
Определение.
Будем
говорить, что функция f(x,y)
![]() раз дифферен цируема в точке Р0
(х0,у0),
если она и все её частные производные
до порядка
раз дифферен цируема в точке Р0
(х0,у0),
если она и все её частные производные
до порядка
![]() включительно определены в некоторой
окрестности
включительно определены в некоторой
окрестности
![]() ,
причём все её частные производные
порядка
,
причём все её частные производные
порядка
![]() дифференцируемы в точке Р0.
дифференцируемы в точке Р0.
Заметим,
что если функция f(x,y)
![]() раз дифференцируема в точке Р0
(х0,у0),
то в этой
точке существуют все частные производные
от f(x,y)
до порядка
раз дифференцируема в точке Р0
(х0,у0),
то в этой
точке существуют все частные производные
от f(x,y)
до порядка
![]() включительно.
включительно.
Теорема
( О
равенстве смешанных частных производных
второго порядка)
Если функция f(x,y)
дважды дифференцируема в точке Р0
(х0,у0),
то справедливо
равенство
![]() .
.
► По
условию
f(x,y)
дважды дифференцируема в точке Р0
(х0,у0),
значит, существует ε
>0, такое,
что в
![]() определены
определены
![]() и
и
![]() ,
причём обе эти функции дифференцируемы
в точке Р0
. Пусть
,
причём обе эти функции дифференцируемы
в точке Р0
. Пусть
![]() -
некото- рое
число. Если
-
некото- рое
число. Если
![]() ,
то точка
,
то точка
![]() содержится
в
содержится
в
![]() .
Везде ниже считаем, что
.
Везде ниже считаем, что
![]() удовлетворяет условию 0
<
удовлетворяет условию 0
<
![]() .
Обозначим:
.
Обозначим:
![]() ,
,
![]() Функция
Функция![]() определена
в некоторой окрестности точки Р0,
а
определена
в некоторой окрестности точки Р0,
а
![]() -
на сегменте, ограниченном точками х0
и х0+
-
на сегменте, ограниченном точками х0
и х0+![]() ,
причем на этом сегменте
,
причем на этом сегменте
![]() .
Запишем приращение
.
Запишем приращение
![]() этой функции:
этой функции:
![]() =
=![]() .=
.=
![]() .
По
формуле конечных приращений
.
По
формуле конечных приращений
![]() ,
где
,
где
![]() -
неко- торое число,
-
неко- торое число,
![]() .
Отсюда:
.
Отсюда:
![]() =
=![]()
![]() .
.
![]() Так как
Так как
![]() дифференцируема в точке Р0,
то
дифференцируема в точке Р0,
то
![]() где
где
![]()
![]() при
при
![]() .
Положив здесь
.
Положив здесь
![]()
![]() ,
получим:
,
получим:
![]()
![]() .
Положим теперь
.
Положим теперь
![]()
![]()
![]() .
Отсюла:
.
Отсюла:
![]()
![]() =
=![]() ,
(17) где
,
(17) где
![]()
![]() -
-![]() .
Заметим:
.
Заметим:
![]() .
.
Положим теперь
![]() ,
и рассмотрим
,
и рассмотрим
![]() :
:
![]() ,
где
,
где
![]() ,
т.е.,
,
т.е.,
![]()
![]() =
=
=![]() =
=
=![]()
Так
как
![]() дифференцируема в точке Р0,
то
дифференцируема в точке Р0,
то
![]() где
где
![]()
![]() при
при
![]() .
Положив здесь
.
Положив здесь
![]()
![]() ,
получим:
,
получим:
![]()
![]()
![]()
![]() Отсюда:
Отсюда:
![]() =
=![]() =
=![]() ,
(18)
,
(18)
где
![]()
![]()
![]() ,
причём
,
причём
![]() .
.
Заметим:
![]() =
=![]() =
=
=![]() .
.
![]()
=![]() .
Таким образом,
.
Таким образом,
![]() =
=![]() .
Отсюда и из (17) и (18) следует: при любых t
таких, что 0 <
.
Отсюда и из (17) и (18) следует: при любых t
таких, что 0 <
![]() справедливо
справедливо
![]() =
=![]() .
Поделив
обе части этого равенства на
.
Поделив
обе части этого равенства на
![]() ,
получим:
,
получим:
![]()
![]() =
=
![]() .
При
.
При
![]() левая часть стремится к нулю; значит,
левая часть стремится к нулю; значит,
![]()
![]() .
◄
.
◄
Следствие. Пусть k,l,m – натуральные числа, причём k+l=m. Если функция f(x,y) m раз дифференцируема в точке Р0, то значение в этой точке любой частной производной порядка m функции f , полученной дифферен-цированием k раз по х и l раз по у, не зависит от порядка, в котором произво- дились последовательные дифференцирования.
Понятие частных производных высших порядков, введенное выше для функций двух переменных, нетрудно обобщить и сформулировать аналогич- ные понятия для функций любого количества переменных.
Пусть
функция
![]() дифференцируема на некотором отк-рытом
множестве Х.
Тогда на
этом множестве определены её частные
произ- водные
дифференцируема на некотором отк-рытом
множестве Х.
Тогда на
этом множестве определены её частные
произ- водные
![]() Если частная производная
Если частная производная
![]() диф- ференцируема, то её частные
производные называют частными производны-
ми второго порядка функции
диф- ференцируема, то её частные
производные называют частными производны-
ми второго порядка функции![]() .
Символами
.
Символами
![]() и
и![]() обозначают производную от
обозначают производную от
![]() по переменной хк
; т.o.
, чтобы найти
по переменной хк
; т.o.
, чтобы найти
![]() ,
нужно сначала
,
нужно сначала![]() продифференцировать
по хi
, а затем
полученную функцию продифференцировать
по хк.
продифференцировать
по хi
, а затем
полученную функцию продифференцировать
по хк.
Частными
производными третьего порядка функции
![]() называют частные производные от её
частных производных второго порядка.
Вообще, частной производной порядка m,
где m
называют частные производные от её
частных производных второго порядка.
Вообще, частной производной порядка m,
где m![]() ,
функции
,
функции
![]() называют частую производную от частной
производной порядка m-1
этой функции; производные
называют частую производную от частной
производной порядка m-1
этой функции; производные
![]() называют при этом частными производными
первого порядка.
Пусть
называют при этом частными производными
первого порядка.
Пусть
![]() -
некоторое натуральное число, не
превышающее m,
-
некоторое натуральное число, не
превышающее m,
![]() -
набор натуральных чисел,
не обязательно
попарно различных, каж- дое из которых
не превышает n
, k1,k2,...,kl
– натуральные числа такие, что их сумма
равна m.
Символом
-
набор натуральных чисел,
не обязательно
попарно различных, каж- дое из которых
не превышает n
, k1,k2,...,kl
– натуральные числа такие, что их сумма
равна m.
Символом
 обозначают частную производ- ную порядка
m,
для вычисления которой
следует
обозначают частную производ- ную порядка
m,
для вычисления которой
следует
![]() сначала продифференцировать α1
раз по переменной
сначала продифференцировать α1
раз по переменной
![]() ,
затем полученную функцию α2
раз
продифференцировать по переменной
,
затем полученную функцию α2
раз
продифференцировать по переменной
![]() и
т.д.
и
т.д.
Определение
8. Будем
говорить, что функция f(x)
= f(x1,x2,…,xn)
m,
где m
> 1, раз дифференцируема в точке х0
![]() Еn
, если
она и все ее частные произ- водные до
порядка m –
1 включительно определены в некоторой
окрестности U
Еn
, если
она и все ее частные произ- водные до
порядка m –
1 включительно определены в некоторой
окрестности U![]() ,
причем все ее производные порядка m
– 1 дифференцируемы в точке х0.
,
причем все ее производные порядка m
– 1 дифференцируемы в точке х0.
Справедливы утверждения :
1) если функция f m раз дифференцируема в точке х0 , то в этой точке суще- ствуют все ее частные производные порядка m ;
2) пусть k1,k2,…,kl – натуральные числа, m = k1+k2 +… + kl ; если функция f m раз дифференцируема в точке х0 , то значения в этой точке всех её частных производных порядка m, полученных дифференцированием k1 раз по x1 , k2 раз по x2 и т. д., kl раз по xl , одинаковы; т.е., значения таких производных не зависят от того, в каком порядке указанные дифференцирования производи- лись.
Определение 9. Будем говорить, что функция f(x) = f(x1,x2,…,xn) m раз, где m >1, непрерывно дифференцируема в точке х0 , если в некоторой окрест- ности этой точки существуют все ее частные производные порядка m, причём эти производные непрерывны в точке х0 .
Определение
10. Будем
говорить, что функция f(x)
= f(x1,x2,…,xn)
m
раз, где
m
>1, непрерывно дифференцируема на
открытом множестве Х![]() Е n
, если
все ее частные производные порядка m
непрерывны на Х
.
Е n
, если
все ее частные производные порядка m
непрерывны на Х
.
-
Дифференциалы высших порядков
Пусть функция f (x,y) m раз, где m > 1, дифференцируема в точке Р0(х0,у0) .
Определение
11. Дифференциалом
порядка m
функции f
(x,y) в точке
Р0
называют
выражение
![]() ,
где h1
и
h2
– переменные,
принимающие независимо друг от друга
любые вещественные значения.
,
где h1
и
h2
– переменные,
принимающие независимо друг от друга
любые вещественные значения.
Переменные
h1
и
h2
называют
приращениями аргументов х
и
у соот-
ветственно,
обозначая
их через
![]() и
и
![]() .
Переменные h1
и
h2
называют
также дифференциалами аргументов х
и
у соответственно,
обозначая
их в этом слу- чае через
.
Переменные h1
и
h2
называют
также дифференциалами аргументов х
и
у соответственно,
обозначая
их в этом слу- чае через
![]() и
и
![]() .
Дифференциал порядка m
функции f
(x,y) в точке
Р0
будем обозначать
через
.
Дифференциал порядка m
функции f
(x,y) в точке
Р0
будем обозначать
через
![]() ,
а также через
,
а также через
![]() или через
или через
![]() .
Таким образом,
.
Таким образом,
![]()
![]() ,
где
,
где
![]() .
.
Для примера запишем дифференциалы второго и третьего порядков:
![]()
![]()
![]()
![]() Pfgbitv
Pfgbitv
![]()
![]()
![]()
![]()
+![]()
Пусть
функция f(x)
= f(x1,x2,…,xn)
m
раз, где
m >1,
дифференцируема в точке х0
![]() ,
х0 =(х10,х20,
…,хn0)
,
х0 =(х10,х20,
…,хn0)
Определение
12. Дифференциалом
порядка m
функции f
(x)
в точке
x0
называют
выражение
 ,
где h1,
h2,
…hn
– переменные,
принимающие независимо друг от друга
любые вещественные значения, a
k1,k2,...kn
–
набор целых неотрицательных чисел
таких, что
,
где h1,
h2,
…hn
– переменные,
принимающие независимо друг от друга
любые вещественные значения, a
k1,k2,...kn
–
набор целых неотрицательных чисел
таких, что
![]() и
и
![]() .
Суммирование
производится по всевозможным наборам
k1,k2,...kn
удовлетво-
ряющих указанным условиям 1) и 2).
.
Суммирование
производится по всевозможным наборам
k1,k2,...kn
удовлетво-
ряющих указанным условиям 1) и 2).
Дифференциал
порядка m
функции f
(x)
в точке x0
будем обозначать
через
![]() ,
а также через
,
а также через
![]() или через
или через
![]() .
При n=
2 дифференциал порядка m,
введенный определением 12, совпадает с
дифференциалом порядка m
функции двух переменных (см. определение
11). Приведём ещё выражение дифференциала
второго порядка функции трёх переменных
.
При n=
2 дифференциал порядка m,
введенный определением 12, совпадает с
дифференциалом порядка m
функции двух переменных (см. определение
11). Приведём ещё выражение дифференциала
второго порядка функции трёх переменных
![]() в
точке Р0(х0,у0,z0):
в
точке Р0(х0,у0,z0):
![]() =
=
![]()
![]()
![]()
+![]()
![]()
![]()
3.8. Формула Тейлора
Теорема 6. Пусть m > 1 и пусть функция f(x) = f(x1,x2,…,xn) m -1 раз диффе- ренцируема в некоторой ε – окрестности точки x0 = (x10,x20, …, xn0) и m раз дифференцируема в самой точке x0 . Тогда для любой точки x, принадлежа- щей указанной ε – окрестности справедлива асимптотическая формула
![]() ,
(19) где
,
(19) где
![]()
Доказательство
этой теоремы можно найти в [1]. Выражение
![]()
![]() представляет
собой алгебраический многочлен степени
не выше m от
n
переменных
x1,x2,…,xn.
Его называют
многочленом Тейлора сте- пени m
функции f(x
) ,
а представление (19) – формулой Тейлора
в точке x0.
В качестве
примера запишем формулу Тейлора при m
=2 для функции f
(x,y) в точке
Р0(х0,у0):
представляет
собой алгебраический многочлен степени
не выше m от
n
переменных
x1,x2,…,xn.
Его называют
многочленом Тейлора сте- пени m
функции f(x
) ,
а представление (19) – формулой Тейлора
в точке x0.
В качестве
примера запишем формулу Тейлора при m
=2 для функции f
(x,y) в точке
Р0(х0,у0):
![]()
![]()

+
![]() .
.
