
- •§ 1. Пространство и его подмножества
- •§ 2. Функция n переменных, ее предел и непрервность
- •§ 3. Частные производные и дифференциал функции n, n2,
- •Обозначают введенную этим определением частную производную символами fх′(m0) или fх′(x0,y0) , а также
- •§ 4. Неявные функции.
- •§ 5. Свободный экстремум функции нескольких переменных
- •Пусть , а - любое, удовлетворяющее условиям . Взяв , удовлетворяющее указанным условиям, выберем для этого число такое, что и обозначим: . Имеем: , причём ;
- •§ 6. Условный экстремум
- •6. 3. Метод Лагранжа
- •В силу инвариантности формы первого дифференциала имеем:
- •Литература
- •§ 1. Пространство и его подмножества
- •Пространство …………………………. 3
- •§ 2. Функция n переменных, её предел и непрерывность
- •§ 3. Частные производные и дифференциалы
- •§ 4. Неявные функции
- •§ 5. Свободный экстремум функции нескольких переменных
- •§ 6. Условный экстремум
§ 1. Пространство и его подмножества
1.1.
Пространство
![]() .
.
Пусть
n
– натуральное число, а х
- упорядоченный набор из n
вещест- венных чисел: х=
( x1,
x2,
… ,xn)
. Набор х
назовем
n–мерным
вектором, а числа, в него входящие, –
координатами этого вектора. Введем
операции сложения векторов, умножения
вектора на вещественное число и скалярного
умножения векторов: если х
= ( x1,
x2,
… ,xn)
и у =
( у1,
у2,
… ,уn)
- два век- тора, x
+ y
- их сумма,
![]() x
- произведение числа
x
- произведение числа
![]() на вектор x,
а (x,y)
– скалярное произведение x
на y,
то
на вектор x,
а (x,y)
– скалярное произведение x
на y,
то
x
+ y
![]() (
x1+
у1, x2+
у2,
… , xn+
уn)
;
(
x1+
у1, x2+
у2,
… , xn+
уn)
;
![]() x
x
![]() (
(![]() x1,
x1,
![]() x2,
… ,
x2,
… ,
![]() xn)
; (1)
xn)
; (1)
(x,y)![]() x1
у1+
x2
у2+…+
xnуn.
x1
у1+
x2
у2+…+
xnуn.
Обозначим
через
![]() совокупность всевозможных n–мерных
векторов, на которой введены описанные
выше операции.
совокупность всевозможных n–мерных
векторов, на которой введены описанные
выше операции.
![]() представляет
собой одну из реализаций n–мерного
эвклидова пространства. Числа x1,
x2
, …, xn
, обра- зующие
набор х
- это координаты элемента x
пространства
представляет
собой одну из реализаций n–мерного
эвклидова пространства. Числа x1,
x2
, …, xn
, обра- зующие
набор х
- это координаты элемента x
пространства
![]() относительно ортонормированного базиса
этого пространства; в качестве базиса
обычно выступает так называемый
стандартный базис – система {e
относительно ортонормированного базиса
этого пространства; в качестве базиса
обычно выступает так называемый
стандартный базис – система {e![]() }
}![]() ,
где e
,
где e![]() -
век- тор, все координаты которого равны
нулю, за исключением к -той координа
-ты, равной единице.
-
век- тор, все координаты которого равны
нулю, за исключением к -той координа
-ты, равной единице.
Определим норму элемента x= ( x1, x2, … ,xn):
||x||
![]()
![]()
![]()
![]() .
.![]()
Свойства нормы известны из курса линейной алгебры.
1.
||x||≥0
; (||x||=0)
![]() ( x=
0 (0,0,
… ,0) ) ;
( x=
0 (0,0,
… ,0) ) ;
2.
||![]() x||
=
x||
=
![]() ||x||
;
||x||
;
3.
|(x,y)|![]() ||x
|| ||y
|| (неравенство
Коши-Буняковского);
||x
|| ||y
|| (неравенство
Коши-Буняковского);![]()
4. ||x +y|| ≤||x|| + ||y|| ( неравенство треугольника ).
В
формулировках определений и теорем
дифференциального исчисле- ния функций
нескольких переменных элементы
пространства
![]() нередко на- зывают не векторами, а точками
пространства
нередко на- зывают не векторами, а точками
пространства
![]() .
Делается это из соображе- ний удобства
речи, а также для того, чтобы в этих
формулировках отчетливее выступали
имеющиеся аналогии с понятиями и
теоремами дифференциаль - ного исчисления
функций одной переменной.
.
Делается это из соображе- ний удобства
речи, а также для того, чтобы в этих
формулировках отчетливее выступали
имеющиеся аналогии с понятиями и
теоремами дифференциаль - ного исчисления
функций одной переменной.
Пусть
х1
= (![]() ,
x
,
x![]() ,
… ,x
,
… ,x![]() )
и х2
= (
)
и х2
= (![]() ,
x
,
x![]() ,
… ,x
,
… ,x![]() )
– два элемента пространства
)
– два элемента пространства
![]() .
Будем говорить, что точка х1
является
началом вектора х2
- х1
= (
.
Будем говорить, что точка х1
является
началом вектора х2
- х1
= (![]() -
-![]() ,x
,x![]() -
x
-
x![]() ,
…
,
…![]()
![]()
![]()
![]() ,
x
,
x![]() -
x
-
x![]() )
, а точка х2
- его концом
; норму этого вектора назовем расстоянием
между точками х1
и
)
, а точка х2
- его концом
; норму этого вектора назовем расстоянием
между точками х1
и ![]()
![]() х2
и обозначим через ρ(х1,
х2)
: ρ(х1,
х2)
х2
и обозначим через ρ(х1,
х2)
: ρ(х1,
х2)
![]() ||х2
- х1||=
||х2
- х1||=
![]() .
Из свойств нормы cледует:
.
Из свойств нормы cледует:
1)
ρ(х1,
х2)
≥ 0 ; ( ρ(х1,
х2)
= 0)
![]() (х1
=х2)
;
(х1
=х2)
;
2![]()
![]() )
ρ(х1
, х
2)
= ρ(х2,
х1)
;
)
ρ(х1
, х
2)
= ρ(х2,
х1)
;
3![]()
![]() )
ρ(х1,
х2)
≤ ρ(х1,
х3)
+ ρ(х3,
х2).
)
ρ(х1,
х2)
≤ ρ(х1,
х3)
+ ρ(х3,
х2).
Пусть
х0
– некоторая точка пространства
![]() ,
а ε – некоторое положи- тельное число.
Множество точек х,
расстояние от которых до х0
меньше ε,
назовем ε- окрестностью точки х0
и обозначим через U
,
а ε – некоторое положи- тельное число.
Множество точек х,
расстояние от которых до х0
меньше ε,
назовем ε- окрестностью точки х0
и обозначим через U![]() (ε)
:
(ε)
:
U![]() (ε)
(ε)
![]() {x
{x![]()
![]() │
ρ(х0,
х)
< ε
}
│
ρ(х0,
х)
< ε
}
Иногда,
называя элемент пространства
![]() точкой, мы будем обозна- чать его большой
буквой латинского алфавита, записывая,
например, P (х1,
х2,
…, хn), что
следует читать: точка P
с координатами х1,х2,
…, хn . Смысл
символов ρ(P1,
P2) и
U
точкой, мы будем обозна- чать его большой
буквой латинского алфавита, записывая,
например, P (х1,
х2,
…, хn), что
следует читать: точка P
с координатами х1,х2,
…, хn . Смысл
символов ρ(P1,
P2) и
U![]() (ε),
употребляемых в таких случаях, понятен
ввиду изложенного выше. “Точечная“
терминология бывает удобной, в частно-
сти, при геометрической интерпретации
понятий и теорем в пространствах
(ε),
употребляемых в таких случаях, понятен
ввиду изложенного выше. “Точечная“
терминология бывает удобной, в частно-
сти, при геометрической интерпретации
понятий и теорем в пространствах
![]() ,
,![]() и
и
![]() .
.
Э![]() лемент
x=
(х)
пространства
лемент
x=
(х)
пространства
![]() представляет собой “набор“, содер-
жащий только одно число х.
Такой элемент удобно представлять
точкой чис- ловой оси с координатой х;
тогда вся числовая ось будет служить
интерпре- тацией пространства
представляет собой “набор“, содер-
жащий только одно число х.
Такой элемент удобно представлять
точкой чис- ловой оси с координатой х;
тогда вся числовая ось будет служить
интерпре- тацией пространства
![]() .
В этой интерпретации норма элемента
x=
(х)
есть модуль числа
х, расстояние
между точками x1=
(х1)
и x2=
(х2)
есть модуль разности их координат:
ρ(х1,
х2)
= |x2-x1|;
ε – окрестность точки x0
=(х0)
- это интервал ( х0
- ε, х0
+ ε).
.
В этой интерпретации норма элемента
x=
(х)
есть модуль числа
х, расстояние
между точками x1=
(х1)
и x2=
(х2)
есть модуль разности их координат:
ρ(х1,
х2)
= |x2-x1|;
ε – окрестность точки x0
=(х0)
- это интервал ( х0
- ε, х0
+ ε).
Упорядоченную
пару (х,у) ( упорядоченную тройку
(x,y,z))
веществен- ных чисел можно расматривать
как декартовы координаты точки, лежащей
на плоскости (находящейся в пространстве).
Это позволяет интерпретировать
пространство
![]() c помощью координатной
плоскости ХОY , а пространство
c помощью координатной
плоскости ХОY , а пространство
![]() представлять совокупностью точек
трехмерного пространства, в котором
введена декартова система координат.
В этой интерпретации норма элемента х
есть расстояние от точки М,
представляющей этот элемент, до начала
ко- ординат, ε – окрестность точки М0
есть круг ( соответственно, шар )
радиуса ε с центром точке М0.
представлять совокупностью точек
трехмерного пространства, в котором
введена декартова система координат.
В этой интерпретации норма элемента х
есть расстояние от точки М,
представляющей этот элемент, до начала
ко- ординат, ε – окрестность точки М0
есть круг ( соответственно, шар )
радиуса ε с центром точке М0.
Удобна
и другая, векторная интерпретация
пространств
![]() ,
,![]() и
и
![]() .
Про- странство
.
Про- странство
![]() можно
представить совокупностью V1
геометрических
векторов (направленных отрезков),
параллельных некоторой оси L.
В этом случае элемент x=
(х)
представлен вектором, проекция которого
на ось L
равна чис- лу х, норма этого элемента
есть |x|,
т.е. длина вектора.
можно
представить совокупностью V1
геометрических
векторов (направленных отрезков),
параллельных некоторой оси L.
В этом случае элемент x=
(х)
представлен вектором, проекция которого
на ось L
равна чис- лу х, норма этого элемента
есть |x|,
т.е. длина вектора.
Упорядоченную
пару (х,у)
( упорядоченную тройку (х,у,z))
веществен- ных чисел можно рассматривать
как координаты в ортонормированном
бази- се i
, j
(в ортонормированном базисе i
, j
, k
) геометрического вектора, лежа- щего
на плоскости (расположенного в
пространстве); операции, введенные
равенствами (1) соответствуют действиям
над геометрическими векторами в векторной
алгебре: сложение векторов, умножение
вектора на число, скаляр- ное умножение
векторов. Поэтому совокупность V2
геометрических
векто -ров, параллельных некоторой
плоскости, можно рассматривать в качестве
интерпретации пространства
![]() ,
а совокупность V3
геометрических векто- ров, расположенных
в пространстве, - в качестве интерпретации
пространст- ва
,
а совокупность V3
геометрических векто- ров, расположенных
в пространстве, - в качестве интерпретации
пространст- ва
![]() .
В этих интерпретациях норма элемента
есть длина геометрического вектора,
представляющего этот элемент.
.
В этих интерпретациях норма элемента
есть длина геометрического вектора,
представляющего этот элемент.
-
Предел последовательности элементов пространства
 .
.
Пусть{xk}
- последовательность точек пространства
![]() ,
а x0
– некоторая точка этого пространства.
,
а x0
– некоторая точка этого пространства.
Определение 1. x0 назовем пределом последовательности {xk}, если ρ(хk, х0) → 0, т.е. если
![]() ρ(хk,
х0)
< ε )
ρ(хk,
х0)
< ε )
Если последовательность {xk} и точка x0 удовлетворяют требованиям этого определения, будем записывать lim xk = x0 или xk→ x0 и будем го- ворить, что последовательность {xk} сходится к. x0 .
Из
определения 1 видно, что при всяком
![]() >0
в
>0
в
![]() -окрестности
U
-окрестности
U![]() (ε)
содержится бесконечное множество членов
последовательности {xk}
, схо- дящейся к.
x0
( именно, все те ее члены, номера которых
превышают
(ε)
содержится бесконечное множество членов
последовательности {xk}
, схо- дящейся к.
x0
( именно, все те ее члены, номера которых
превышают
![]() ),
а вне U
),
а вне U![]() (ε)
может находиться разве лишь конечное
количество ее членов. Напомним, что
такой же фразой можно характеризовать
и поведение число- вой последовательности
{xk},
сходящейся к числу х0
( [2], п.
3.2), так что предел числовой последовательности
и предел последовательности элемен-
тов
(ε)
может находиться разве лишь конечное
количество ее членов. Напомним, что
такой же фразой можно характеризовать
и поведение число- вой последовательности
{xk},
сходящейся к числу х0
( [2], п.
3.2), так что предел числовой последовательности
и предел последовательности элемен-
тов
![]() -
понятия аналогичные . Аналогичны и
формулировки их основных свойств. Можно
сказать, что теоремы о сходящихся
числовых последова- тельностях ( [2],
п.п. 3.3, 3.4) справедливы и для
последовательностей в
-
понятия аналогичные . Аналогичны и
формулировки их основных свойств. Можно
сказать, что теоремы о сходящихся
числовых последова- тельностях ( [2],
п.п. 3.3, 3.4) справедливы и для
последовательностей в
![]() ,
за исключением
тех из них,
которых касаются неравенств – для
элементов
,
за исключением
тех из них,
которых касаются неравенств – для
элементов
![]() отношения
″больше″ или ″меньше″ не определены.
отношения
″больше″ или ″меньше″ не определены.
Пусть
задана последовательность {xk}![]() ,
xk
= (
,
xk
= (
![]() )
. Рассмот- рим последовательности,
образованные первыми координатами
векторов xk
, их вторыми
координатами и т.д. , их n
-ными координатами:
)
. Рассмот- рим последовательности,
образованные первыми координатами
векторов xk
, их вторыми
координатами и т.д. , их n
-ными координатами:
{x![]() }
}![]() , {x
, {x![]() }
}![]() , … , {x
, … , {x![]() }
}![]()
Теорема
1.
( О покоординатной
сходимости)
Пусть задана последо- вательность
{xk}![]() ,
xk
= (
,
xk
= (
![]() )
и точка x0
= (
)
и точка x0
= (
![]() )
. Для то- го, чтобы последовательность
{xk}
)
. Для то- го, чтобы последовательность
{xk}![]() сходилась к x0
,
необходимо и достато- чно, чтобы
последовательность {x
сходилась к x0
,
необходимо и достато- чно, чтобы
последовательность {x![]() }
}![]() сходилась к х10
, {x
сходилась к х10
, {x![]() }
}![]() сходилась к х20
и т.д.,
последовательность {x
сходилась к х20
и т.д.,
последовательность {x![]() }
}![]() сходилась к xn0
:
сходилась к xn0
:
(xk→
x0
)
![]() (x
ik→
x
i0
,
i = 1,2,…,n )
(x
ik→
x
i0
,
i = 1,2,…,n )
► В
силу определения 1 xk→
x0
означает
ρ(хk,
х0)
→ 0 , т. е.
![]() , что, очевидно, имеет место тогда и
только тогда, когда каждая из скобок
в подкоренном выражении стремит- ся к
нулю, т.е.
, что, очевидно, имеет место тогда и
только тогда, когда каждая из скобок
в подкоренном выражении стремит- ся к
нулю, т.е.
![]() при i
= 1,2, …, n
. ◄
при i
= 1,2, …, n
. ◄
Теорема 2. (О единственности предела) Сходящаяся последователь- ность имеет только один предел.
►
Допустим,
что xk→
x0
и xk→
у0
, где x0
= (
![]() ),
у0
= (у10,
у
),
у0
= (у10,
у![]() ).
В силу теоремы 1 x1k→
x10
и
x1k→
у10.
Но для числовых последовательностей
справедлива теорема о единственности
предела ( [2], п. 3.2), поэтому х10
= у10.
Аналогично докажем, что и другие
координаты точки у0
совпадают
с соответствующими координатами точки
x0
.
Значит, x0
= у0
. ◄
).
В силу теоремы 1 x1k→
x10
и
x1k→
у10.
Но для числовых последовательностей
справедлива теорема о единственности
предела ( [2], п. 3.2), поэтому х10
= у10.
Аналогично докажем, что и другие
координаты точки у0
совпадают
с соответствующими координатами точки
x0
.
Значит, x0
= у0
. ◄
Теорема 3. ( О действиях над сходящимися последовательностями)
Пусть xk→ x0 и уk→ у0 . Тогда 1) xk + yk → x0 + y0 , 2) λ xk → λ x0 (здесь λ – любое число) , 3) (xk, уk) → (x0 , у0) .
► Пусть xk = ( х1k,x2k, …, xnk) , yk = ( y1k,y2k, …, ynk) , x0 = ( х10,x20, …, xn0), y0 = (y10,y20, …, yn0). 1) Имеем: xk+yk = ( x1k+y1k, x2k+y2k, …, xnk +ynk), x0 + y0 = ( x10+y10, x20+y20, … , xn0+yn0) . По теореме 1 из xk→ x0 и уk→ у0 следует xik → xi0 и уik → уi0 при i = 1,2,…,n ; значит, по теореме об ариф- метических действиях со сходящимися числовыми последовательностями ( [2], п. 3.3) xik+yik → xi0+yi0 при i = 1,2,…,n . Снова обращаясь к теореме 1, отсюда получаем : xk + yk → x0 + y0 . Доказательства утверждений 2) и 3) аналогичны. ◄
Определение 2. Последовательность {αk} называют бесконечно малой последовательностью, если ее предел равен нулевому вектору 0(0,0,… …,0).
Справедливы
утверждения : 1) если {αk}
и {βk}
- бесконечно
малые последовательности
, то
{ αk+
βk}
и
{λαk}
, где λ – любое вещественное число, также
бесконечно малые последовательности;
2) (αk→
0)
![]() (
||αk||→
0 ); З) пусть {xk}-
некоторая последовательность, а x0
- некоторая точка: тогда ( xk→
x0
)
(
||αk||→
0 ); З) пусть {xk}-
некоторая последовательность, а x0
- некоторая точка: тогда ( xk→
x0
)
![]() (
xk-
x0
→ 0 ).
(
xk-
x0
→ 0 ).
Упражнение. Доказать утверждения 1) – 3).
1.3.
Множества
в
![]() .
.
Пусть
Х
- некоторое множество точек пространства
![]() ,
а х0
– некото-
рая точка этого пространства.
,
а х0
– некото-
рая точка этого пространства.
Определение
1. х0
назовем
внутренней точкой множества Х,
если
существует ε-окрестность U![]() (ε),
целиком содержащаяся в Х.
(ε),
целиком содержащаяся в Х.
Определение
2. х0
назовем
граничной точкой множества Х,
если в любой
ε-окрестности U![]() (ε)
содержатся хотя бы одна точка множества
Х
и хотя бы одна точка, Х
не
принадлежащая.
(ε)
содержатся хотя бы одна точка множества
Х
и хотя бы одна точка, Х
не
принадлежащая.

![]() x1.
x1.
![]() x2
Замечание. Внутренняя
точка множества Х
принадле-
x2
Замечание. Внутренняя
точка множества Х
принадле-
жит Х. Граничная точка множества Х может принадле-
жать, но может и не принадлежать Х.
Рис.1
На рис.1 плоская фигура
представляет множество Х
, лежащее в
![]() ;
х1
– внутренняя
точка Х,
а х2
– его
граничная точка.
;
х1
– внутренняя
точка Х,
а х2
– его
граничная точка.
Определение
3. х0
называют
предельной точкой множества Х,
если всякая
ε-окрестность U![]() (ε)
содержит хотя бы одну точку множества
Х,
отличную от х0
.
(ε)
содержит хотя бы одну точку множества
Х,
отличную от х0
.
Определение
4. х0
называют
изолированной точкой множества Х,
ес- ли
существует ε-окрестность U![]() (ε)
такая, что х0
является
единственной точ- кой этой окрестности,
принадлежащей Х.
(ε)
такая, что х0
является
единственной точ- кой этой окрестности,
принадлежащей Х.
Замечание. Предельная точка множества Х может принадлежать, но может и не принадлежать Х. Изолированная точка множества Х принадле-жит Х.
Пример
1. Пусть Х
есть множество
точек М(х,у) , координаты кото- рых
удовлетворяют уравнению
![]() .
Очевидно, Х
состоит из
начала координат О(0,0) и точек окружности
радиуса единица с центром в О. Точки
окружности – предельные точки множества
Х,
О – его изолирован- ная точка.
.
Очевидно, Х
состоит из
начала координат О(0,0) и точек окружности
радиуса единица с центром в О. Точки
окружности – предельные точки множества
Х,
О – его изолирован- ная точка.
Упражнение. Доказать следующие утверждения. 1) Всякая принадлежащая множеству Х точка является либо его внутрен- ней, либо его граничной точкой. 2) Всякая принадлежащая множеству Х точка является либо его предель- ной, либо его изолированной точкой . 3) х0 является предельной точкой множества Х тогда и только тогда, когда существует сходящаяся к х0 последовательность, все члены которой принад- лежат Х и отличны от х0 . 4) Внутренняя точка множества является его предельной точкой. 5) Изолированная точка множества является его граничной точкой. 6) Граничная точка множества является либо его предельной, либо его изолированной точкой.
Определение 5. Х называют открытым множеством, если каждая его точка является внутренней точкой этого множества.
Определение 6. Х называют замкнутым множеством, если ему при- надлежат все его предельные точки.
Замечание. Множество, содержащее все свои граничные точки, явля- ется замкнутым. Множество, не содержащее ни одной из своих граничных точек, является открытым.
Пример
2. Пусть Х1
= { M(x,y)|
![]() }
, X2
= { M(x,y)|
}
, X2
= { M(x,y)|
![]() },
X3
= {M(x,y)|
},
X3
= {M(x,y)|
![]() }.
Здесь Х1
– открытое
множество, так как не содержит граничных
точек ( точек единичной окружности). X2
– замкнутое множество, так как содержит
все свои граничные точки. Множество X3
не является
ни открытым, ни замкнутым, ибо часть его
граничных точек ему принадлежит (точки
верхней половины единичной окружности),
а другая их часть (точки интервала (-1,1)
оси абсцисс) Х3
не принадлежит.
}.
Здесь Х1
– открытое
множество, так как не содержит граничных
точек ( точек единичной окружности). X2
– замкнутое множество, так как содержит
все свои граничные точки. Множество X3
не является
ни открытым, ни замкнутым, ибо часть его
граничных точек ему принадлежит (точки
верхней половины единичной окружности),
а другая их часть (точки интервала (-1,1)
оси абсцисс) Х3
не принадлежит.
Определение
7. Совокупность
всех внутренних точек множества Х
называют
внутренностью множества Х
и обозначают
через
![]() .
Совокуп- ность всех граничных точек
множества Х
называют
его границей и обо -значают через
.
Совокуп- ность всех граничных точек
множества Х
называют
его границей и обо -значают через
![]() .
.
Определение 8. Х называют ограниченным множеством, если существует М > 0 такое, что норма любого элемента Х не превышает М. Множество, не являющееся ограниченным, называют неограниченным.
1.4.
Линии
в
![]() .
.
Напомним
основные понятия, касающиеся непрерывных
плоских кри- вых ( [1], § 17). Пусть функции
х(t)
и у(t)
определены на некотором проме- жутке
![]()
![]() .Обозначим
через Рt
точку
плоскости с абсциссой х(t)
и ординатой у(t)
, а через γ
– упорядоченную совокупность {Рt}
этих точек, где t
пробегает, возрастая весь промежуток
.Обозначим
через Рt
точку
плоскости с абсциссой х(t)
и ординатой у(t)
, а через γ
– упорядоченную совокупность {Рt}
этих точек, где t
пробегает, возрастая весь промежуток
![]() .
Упорядоченность γ
означает, что при любых t1
и
t2
, t1<
t2
, принадлежащих
.
Упорядоченность γ
означает, что при любых t1
и
t2
, t1<
t2
, принадлежащих
![]() ,
точка Рt
,
точка Рt![]() считается
пред- шествующей точке Рt
считается
пред- шествующей точке Рt![]() .
Прибегая к геометрической интерпретации,
можно сказать, что γ
– это траектория, которую описывает на
плоскости точка Рt
при возрастании t
от α
до β.
γ
называют непрерывной плоской кривой,
а систему
.
Прибегая к геометрической интерпретации,
можно сказать, что γ
– это траектория, которую описывает на
плоскости точка Рt
при возрастании t
от α
до β.
γ
называют непрерывной плоской кривой,
а систему
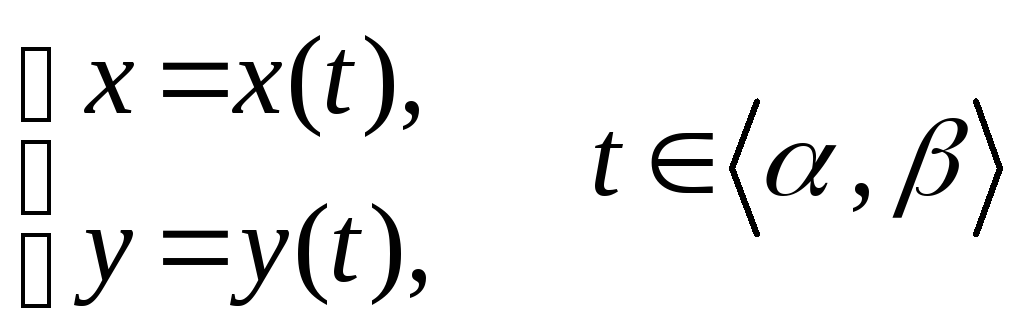 - параметрическими уравнениями кривой
γ.
γ
есть годог- раф вектор-функции r(t)
= x(t)
i
+ y(t)
j
;
параметрические уравнения γ
мож- но записать в векторной форме : r
= r(t)
,
- параметрическими уравнениями кривой
γ.
γ
есть годог- раф вектор-функции r(t)
= x(t)
i
+ y(t)
j
;
параметрические уравнения γ
мож- но записать в векторной форме : r
= r(t)
,
![]() ,
где r
= xi
+ + yj
. Если
промежуток
,
где r
= xi
+ + yj
. Если
промежуток
![]() представляет собой сегмент, то точку А
= Р
представляет собой сегмент, то точку А
= Р![]() называют началом кривой γ,
а точку В=Р
называют началом кривой γ,
а точку В=Р![]() -
ее концом; говорят также, что непрерывная
кривая γ
соединяет точки А и В.
-
ее концом; говорят также, что непрерывная
кривая γ
соединяет точки А и В.
Пусть
Р0(х0,у0)
– заданная точка, а s
= s1i
+ s2j
- заданный
вектор. Система
 есть параметрические уравнения прямой,
проходящей через точку Р0
параллельно вектору s
.
есть параметрические уравнения прямой,
проходящей через точку Р0
параллельно вектору s
.
Опишем
аналогичные понятия в пространстве
![]() любой
размерности n≥2.
Пусть функции xi(t),
i
= 1,2,…,n,
непрерывны на промежутке
любой
размерности n≥2.
Пусть функции xi(t),
i
= 1,2,…,n,
непрерывны на промежутке
![]() ,
,
![]() .
Обозначим через Рt
точку с координатами (x1(t),
x2(t),
…, xn(t)),
а через γ
– упорядоченную совокупность { Рt}
этих точек, где t
пробегает, возрастая, промежуток
.
Обозначим через Рt
точку с координатами (x1(t),
x2(t),
…, xn(t)),
а через γ
– упорядоченную совокупность { Рt}
этих точек, где t
пробегает, возрастая, промежуток
![]() .
Упорядоченность γ
понимается так же, как выше. γ
назовем непрерывной кривой в
.
Упорядоченность γ
понимается так же, как выше. γ
назовем непрерывной кривой в
![]() ,
а систему
,
а систему
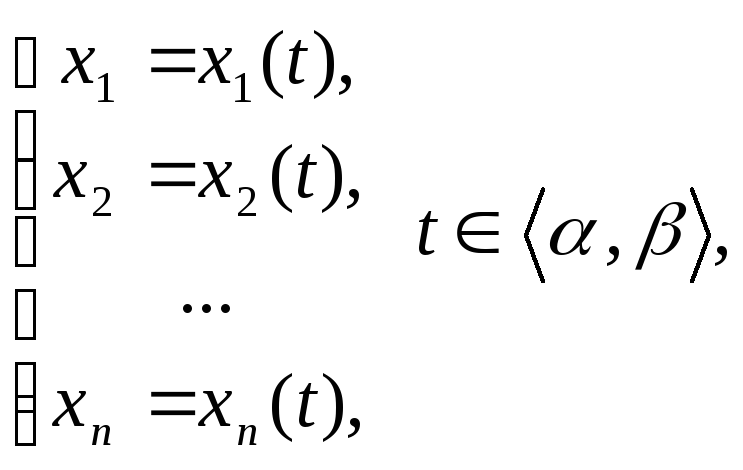 (1)
(1)
-
параметрическими уравнениями γ.
Введя обозначения r
= ( x1,x2,
…,xn)
, r(t)
= (x1(t),
x2(t),
…, xn(t))
, систему (1) можно записать в векторной
форме: r
= r(t),
![]() .
В дальнейшем запись γ
= { r
= r(t),
.
В дальнейшем запись γ
= { r
= r(t),
![]() }
следу- ет читать так: γ
- непрерывная кривая, заданная уравнениями
(1) или r
=r(t),
}
следу- ет читать так: γ
- непрерывная кривая, заданная уравнениями
(1) или r
=r(t),
![]() .
.
Пусть
Р0(
x10,x20,
…,xn0)
- заданная точка, а s
= (s1,s2,
…,sn)
– заданный вектор. Линию, заданную в
![]() уравнениями
уравнениями

называют прямой линией ; она проходит через точку Р0 и параллельна век-тору s .
Если
промежуток
![]() есть сегмент, А = Р
есть сегмент, А = Р![]() ,
В = Р
,
В = Р![]() ,
то точку А будем называть началом кривой
γ,
заданной уравнениями (1), а точку В –
концом этой кривой. Будем также говорить,
что непрерывная кривая γ
сое- диняет точки А и В.
,
то точку А будем называть началом кривой
γ,
заданной уравнениями (1), а точку В –
концом этой кривой. Будем также говорить,
что непрерывная кривая γ
сое- диняет точки А и В.
Определение
1. Множество
![]() назовем связным множеством, если любые
две его точки можно соединить непрерывной
кривой, все точки которой принадлежат
Х.
назовем связным множеством, если любые
две его точки можно соединить непрерывной
кривой, все точки которой принадлежат
Х.
Определение 2. Областью будем называть любое связное открытое множество .
