36. Изложить способы задания плоскости в пространстве и вывести различные виды уравнений плоскости в зависимости от способа ее задания..

Плоскость в пространстве может быть задана:

1) точкой и вектором перпендикулярным плоскости

2) тремя точками

3) отрезками, отсекаемыми плоскостями на осях координат

4) точкой и двумя неколлинеарными векторами параллельными плоскости

Виды уравнений плоскости в пространстве:

-1-)

-2-) A(х-х₀)+В(у-у₀)+С(z-z₀)=0 -- уравнение плоскости проходящей через данную точку перпендикулярно данному вектору.

-3-) Aх+ Ву+ Сz+D=0 -- общее уравнение плоскости

37. Разъяснить критерии определения взаимного расположения плоскостей в пространстве, записать условия их параллельности и перпендикулярности. Записать формулу для определения угла между плоскостями и расстояния от точки до плоскости.

Взаимное расположение плоскостей в пространстве:

Две плоскости в пространстве либо параллельны, либо пересекаются, либо перпендикулярны.

Условие параллельности:

р₁//р₂  n1(вектор)↑↓n2(вектор)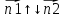  A1/A2=B1/B2=C1/C2

Условие совпадения:

р₁=р₂  A1/A2=B1/B2=C1/C2=D1/D2 …. A1/A2 не равно B1/B2(В1/B2 не равно C1/C2) пересекаются

Условие перпендикулярности:

р1┴р2 тогда и только тогда, когда перпендикулярны их нормальные вектора

А₁А₂+В₁В₂+С₁С₂=0

Плоскости, пересекаясь, образуют четыре двугранных угла: два тупых и два острых или четыре прямых, причем оба тупых угла равны между собой, и оба острых тоже равны между собой. Для определения его величины возьмем точку M на линии пересечения плоскостей и в этой точке в каждой из плоскостей проведем перпендикуляры L₁ и L₂ к линии пересечения. Нарисуем также нормальные векторы n₁ и n₂ плоскостей П₁и П ₂ с началами в точке М.

Если через точку M провести плоскость П, перпендикулярную линии пересечения плоскостей П₁и П ₂, то прямые L₁ и L₂ и изображения векторов n₁ и n₂ будут лежать в этой плоскости. косинус острого угла между плоскостями.

Пусть плоскость П,задана уравнением Ax+By+Cz+D=0 и дана точка M_o(X_o;Y_o; Z_o) . Тогда расстояние p от точки M_o до плоскости П определяется по формуле

38. Изложить способы задания прямой в пространстве и вывести различные виды уравнений прямой в пространстве в зависимости от способа ее задания.

Прямая в пространстве может быть задана:

1) точкой и направляющим вектором

2) двумя точками

3)пересечением двух плоскостей

Уравнения:

; t∊R -- векторное уравнение прямой

x-x₀/a₁=y-y₀/a₂=z-z₀/a₃ -- каноническое уравнение прямой

x-x₁/x₂-x₁=y-y₁/y₂-y₁=z-z₁/z₂-z₁-- уравнение прямой по двум точкам

39. Разъяснить критерии взаимного расположения прямых в пространстве и записать различные условия их взаимного расположения.

Взаимное расположение прямых на плоскости.

A₁/ A₂= B₁/ B₂ =C₁/ C₂ (две прямые на плоскости либо пересекаются в одной точке либо совпадают либо параллельны)

Условия параллельности совпадает с условием коллинеарности векторов: A₁/A₂= B₁/B₂=C₁/C₂

Условия перпендикулярности равносильно условию перпендикулярности их направляющих векторов a₁ a₂ A₁*A₂+ B₁*B₂+ C₁*C₂