
- •Отчет по радиологии
- •Задание №1
- •Задание №2
- •График зависимости концентрации радона от времени
- •Задание №3
- •Задача №4
- •График зависимости концентрации от мощности наносов, перекрывающих урансодержащий пласт
- •Задание № 5
- •Расчёт дозы излучения - излучения 4 - среды для гранитов.
- •2. Расчёт дозы излучения - излучения 4 - среды для известняков.
- •Задание № 6
- •Расчет γ – поля вне пласта.
- •Задание №7
- •Задание №8
- •Задание №9
- •Функция пропускания γ-лучей.
- •График зависимости функции пропускания γ –лучей от мощности пласта
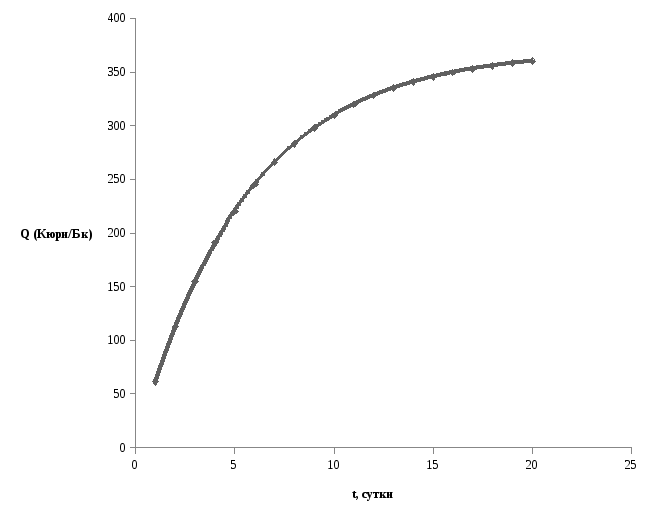
График зависимости концентрации радона от времени
Задание №3
Условие: рассчитать концентрацию Rn в объемном пласте конечной мощности, выходящего на дневную поверхность.
Исходные
данные:
H=2м;
Pu=0,05;
L=1м;
p0=2,3
г/см3;
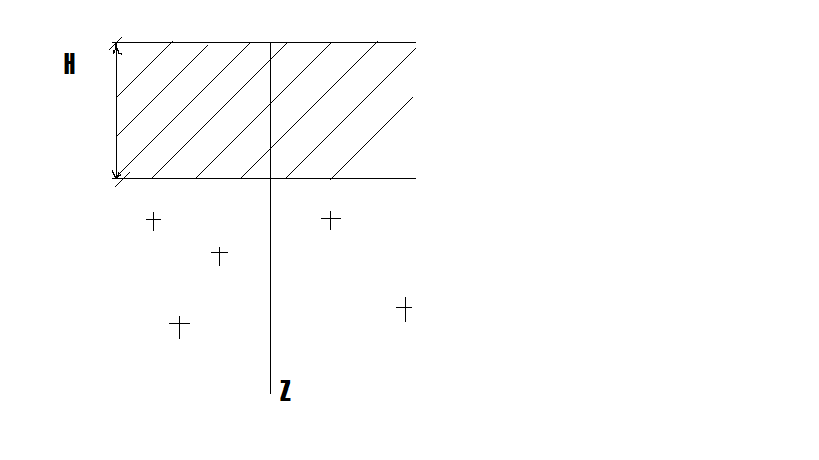
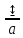 =1
=1
Распределение
концентрации радиоактивной эманации
в пределах мощности активного пласта
С(Z;H).
Для случая, установившегося во t
режима (
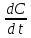 =0)
и при отсутствии конвективного переноса
(D=0)
дифференциальное уравнение переноса
выглядит
следующим образом:
=0)
и при отсутствии конвективного переноса
(D=0)
дифференциальное уравнение переноса
выглядит
следующим образом:
 С=
С=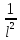 C=-
C=-
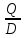
Где Q – количество эманаций, выделяющих в поровое пространство единицы объема пласта в единицу времени;
D - коэффициент диффузии радиоактивной эманации; L – диффузионная длина.
Поскольку
пласт по горизонтальным осям бесконечен,
то в случае однородного распределения
активных компонентов градиенты
концентрации по осям X,Y
будут равны 0, т.е.
 С=
С=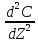 тогда
тогда
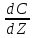 -
-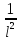 C
=-
C
=-
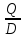 .
Для решения дифференциального уравнения
необходимы граничные условия:
.
Для решения дифференциального уравнения
необходимы граничные условия:
-
Концентрация эманации в воздухе обычно нескольких порядков меньше концентрации в поровом пространстве горных пород, С=0 при Z=0;
-
Будем считать подстилающие породы настолько плотными (очень малая пористость), что эманация не будет в них диффундировать, т.е.
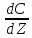 =0,
при Z=11
=0,
при Z=11
Решая дифференциальное уравнение с учетом граничных условий получим:
С(Z,H)
=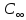
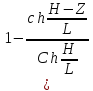 ]
]
Где
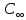 -
концентрация в любой точке однородного
4π-активного пространства.
-
концентрация в любой точке однородного
4π-активного пространства.
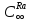 =3,4∙104
=3,4∙104
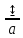 p0pu(эман)
p0pu(эман)
Где pu- массовая доля урана, %
p0 – плотность радиоактивного пласта, г/см3.
При
заданных условиях
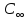 =3,4∙104∙1∙2,3∙0,05=0,391∙104[эман]
=3,4∙104∙1∙2,3∙0,05=0,391∙104[эман]
[1
эман =3,7∙103
Бк/м3],
тогда
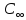 =1,447∙107
Бк/м3
=1,447∙107
Бк/м3
При расчете концентрации радона используется шаг равный 0,2м
-
Z=0, C(Z;H)=0
-
Z=0, 2 Ch
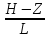 =
2-0,2/1=Ch 1,8=3,08
=
2-0,2/1=Ch 1,8=3,08
Ch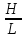 =
=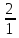 =Ch2=3,72
=Ch2=3,72
C(Z,H)=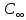 [1-
[1-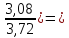 0,249∙107
Бк/м3
0,249∙107
Бк/м3
-
Z=0,4 Ch
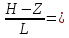 2-0,4/1=Ch1,6=2,6
2-0,4/1=Ch1,6=2,6
C(Z,H)=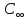 [1-
[1-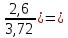 0,435∙107
Бк/м3
0,435∙107
Бк/м3
-
Z=0,6 Ch
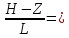 2-0,6/1=Ch1,4=2,16
2-0,6/1=Ch1,4=2,16
C(Z,H)=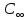 [1-
[1- 0,607∙107
Бк/м3
0,607∙107
Бк/м3
-
Z=0,8 Ch
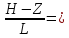 2-0,8/1=Ch1,2=1,82
2-0,8/1=Ch1,2=1,82
C(Z,H)=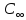 [1-
[1-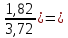 0,739∙107
Бк/м3
0,739∙107
Бк/м3
-
Z=1 Ch
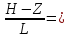 2-1/1=Ch1=1,55
2-1/1=Ch1=1,55
C(Z,H)=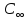 [1-
[1-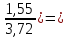 0,844∙107
Бк/м3
0,844∙107
Бк/м3
-
Z=1,2 Ch
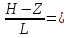 2-1,2/1=Ch0,8=1,34
2-1,2/1=Ch0,8=1,34
C(Z,H)=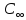 [1-
[1-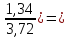 0,925∙107
Бк/м3
0,925∙107
Бк/м3
-
Z=1,4 Ch
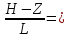 2-1,4/1=Ch0,6=1,19
2-1,4/1=Ch0,6=1,19
C(Z,H)=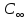 [1-
[1-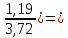 0,984∙107
Бк/м3
0,984∙107
Бк/м3
-
Z=1,6 Ch
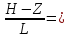 2-1,6/1=Ch0,4=1,08
2-1,6/1=Ch0,4=1,08
C(Z,H)=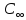 [1-
[1-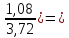 1,027∙107
Бк/м3
1,027∙107
Бк/м3
-
Z=1,8 Ch
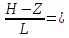 2-1,8/1=Ch0,2=1,02
2-1,8/1=Ch0,2=1,02
C(Z,H)=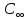 [1-
[1-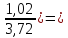 1,051∙107
Бк/м3
1,051∙107
Бк/м3
-
Z=2 Ch
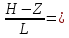 2-2/1=Ch0=1
2-2/1=Ch0=1
C(Z,H)=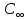 [1-
[1-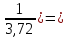 1,058∙107
Бк/м3
1,058∙107
Бк/м3
Зависимость концентрации радона от мощности пласта:
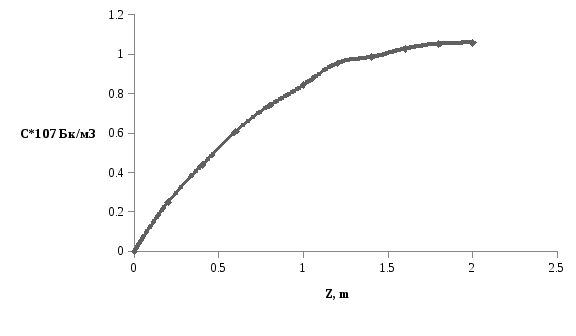
Вывод: с увеличением мощности радиоактивного пласта, выходящего на дневную поверхность, увеличивается в нем концентрация радона.
Задача №4
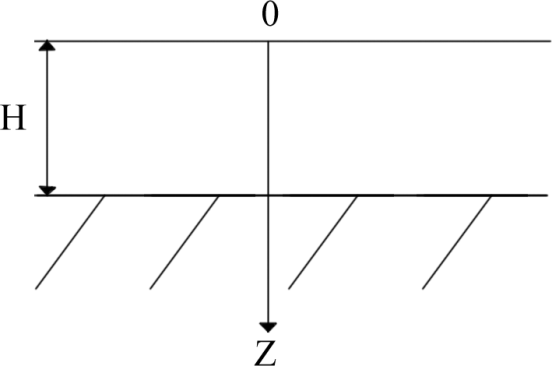
Условие: расчет поведения концентрации радона в чехле наносов конечной мощности, перекрывающих урансодержащий пласт бесконечной мощности.
Исходные
данные:
Н=2м; L=1м;
![]() =2,6
г/
=2,6
г/![]() ;
;
![]() =0,05%;
η=15%; η=α
=0,05%;
η=15%; η=α
При
поиски распределения концентрации
радиоактивности эманации в пределах
мощности чехла считают, что источники
эманации в насосах отсутствуют. Задача
ограничивается стандартным случаем,
т.е.:
![]()
Предположим,
что скорость конвективного переноса
V=0,
записывается уравнением переноса: С-![]()
Поскольку,
по горизонтальным осям градиент
концентрации радиоактивного компонента
равен нулю, то уравнение переноса будет
однородным, т.е.:
![]()
Граничные условия:
-
При Z=0, С=0;
-
Поток эманации через единицу поверхности контакта(полагается, что через границу раздела чехол-пласт плоская, горизонтальная и безграничная) в единицу времени составляет j [Бк/
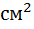 ]
, тогда второе граничное условие j=D
dC/dZ
при z=H
]
, тогда второе граничное условие j=D
dC/dZ
при z=H
В итоге получаем:
С(Z,H)=C(Z,H)=
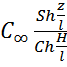 ;
;
где
![]() -
концентрации в любой точке однородного
4-х активного пространства:
-
концентрации в любой точке однородного
4-х активного пространства:
![]() =
3,13∙
=
3,13∙![]()
![]() [эман]
[эман]
где
![]() -
массовая доля урана, %;
-
массовая доля урана, %;
![]() -
плотность радиоактивного пласта, г/
-
плотность радиоактивного пласта, г/![]()
Для заданных условий:
![]() =
0,05%
=
0,05%
![]() 3,4∙
3,4∙![]() ∙1∙2,3∙0,05=0,391∙
∙1∙2,3∙0,05=0,391∙![]() [эман]=1,447∙
[эман]=1,447∙![]() Бк/
Бк/![]()
Shx-
гиперболический синус, Shx=
![]() ,
,
Сhx-
гиперболический косинус, Сhx=![]()
При расчете использовался шаг, равный 0,2м. Результаты расчета представлены в таблице.
Таблица
№2. Результаты расчета концентрации
![]()
|
Z,м |
С, |
|
0,2 |
0,078 |
|
0,4 |
0,161 |
|
0,6 |
0,249 |
|
0,8 |
0,346 |
|
1 |
0,460 |
|
1,2 |
0,591 |
|
1,4 |
0,746 |
|
1,6 |
0,931 |
|
1,8 |
1,154 |
|
2 |
1,423 |
