Министерство
Образования и Науки РФ
ФГБОУ ВПО
Уральский государственный горный
Университет
Факультет геологии и геофизики
Кафедра ядерной геофизики и радиометрии
Отчет по радиологии
Студентка группы ИЗС–10 (Фамилия И.О.)
Проверил (Возжеников Г.С.)
Екатеринбург
2011
Задание №1
Условие: рассчитать величину удельных активностей по торону и калию в любой точке природных сред (граниты и известняки),при условиях:
Исходные данные: В гранитах PU=3,6 г/т, PTh=15,5 г/т, PK=3,6%,U=4,5∙109 лет,Th=1,4∙1010 лет,K1940=1,27∙109 лет.
Активность-
количественное понятие
.
Решение:
A=
,
a=λ∙ n(p/c)
1p/c=1Бк,А=
(Бк/кг),где
,m=1
кг
a(t)=λ∙n0∙e-λt
a(t)
=λ∙n0∙e-ln2
,
t<<T,n=
∙3,6∙10-3,
N0-Число Авогадро (6,02∙1023)
А-массовое число:1023
Граниты
AU=238, ATh=232, AK=39
AU=
∙3,6∙10-3
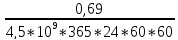=44,27(Бк/к)
ATh=
∙15,5∙10-3
=62,85(Бк/кг)
AK=
∙3,6∙103∙10-4
=957,35(кБк/кг)
Известняки
Исходные данные:PU=1,2г/т,PTh=2,5г/т,PK=0,4%
Решение:
AU=
∙1,2∙10-3
=14,76(Бк/
кг)
ATh=
∙2,5∙10-3
=101,38(Бк/кг)
AK=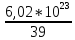
∙4∙103∙10-4
=106,37(кБк/
кг)
-
Удельная суммарная активность в строительных материалах
-
Материалы использующиеся в дорожном строительстве, в населенных пунктах (2 класс)
-
Материалы использующиеся в дорожном строительстве вне населенных пунктов(1 класс)
Задание №2
Условие: рассчитать поведение концентрации Rn, в герметичной полости.
Исходные данные: V=1л; t=Var(0-20 сут); mRa = 10-8 г; 1гU = 3,4 ∙10-7 г Ra, TRn = 3,825 суток, Q Ra =370 Кюри/Бк
Решение:
n2(t)? n1(t)→n2(t)
За t dt образуется ядер λ1n1dt распалось λ2n2dt
λ1n1dt - λ2n2dt
+
λ2n2=
λ1n01e-
t
–
исходное дифференциальное уравнения
Λ2- постоянная распада дочернего продукта
n2t= n2’+n2’’ n2’ –общее решение n2’’ – частное решение
-λ1Beλ1t
+
λ2Be-λ1t
=
λ1n01e-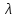
t
-λ1B + -λ2B= λ1n01
B (λ2 - λ1) = λn01
B
=
O=B+A;
A=-B; A = -
n2(t)
=
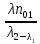(e
-λ1t
–e
-λ2t)
Ra
→ Rn λ1
2
n2
(t)
=
n01
e -λ1t
[1-
e -λ2t]
n(t)=exp(-λt) –закон распада
n01 e -λ1t =n1t
n(t)/n0 – функция выживания
n(t)/n0 = exp(-λt), λ – параметр постоянного распада
2
n2
(t)
– активный дочерний продукт
2
n2
(t)=
λ1n1(t)
-[1-
];
a2(t)
= a1(t)
-[1-
];
n(t)=n0
];
= K
=
→T=
T=
=
→
=
2
n2
(t)=
λ1n1(t)
-[1-
];
K
T2
→
2
n2
(t)=
λ1n1(t)
– радиоактивное
равновесие
=
[1-
];
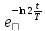Найдем t максимальное:
=
[n2(t)]
= 0
-λ1
+
λ2
=0
λ1
=
λ2
=
(λ2
-
λ1)
Ln
= -
(
λ2
-
λ1)
=
λ1 =λRa= 1,373∙10-11,(c-1)
λ1 =λRn= 2,098∙10-6,(c-1)
=
,
(c-1)
= 1468,1 [час]= 61, 2 [сут]
1 Кюри = 3, 7∙1010[P/c], [Бк]; 1 Кюри = 1гRa
3,7∙1010∙10-8 = 370 [Кюри/Бк]
QRn
=370-
= 370[Кюри/Бк]
Составим зависимость концентрации радона от времени, при t варьирующем от 0-20 суток.
|
t, сутки |
QRn, Кюри/Бк |
|
1 |
61,32 |
|
2 |
112,47 |
|
3 |
155,17 |
|
4 |
190,77 |
|
5 |
220,47 |
|
6 |
245,26 |
|
7 |
265,93 |
|
8 |
283,18 |
|
9 |
297,57 |
|
10 |
309,58 |
|
11 |
319,60 |
|
12 |
327,95 |
|
13 |
334,93 |
|
14 |
340,73 |
|
15 |
345,58 |
|
16 |
349,63 |
|
17 |
353,01 |
|
18 |
355,82 |
|
19 |
358,17 |
|
20 |
360,13 |