§ 5.4. Определение области срабатывания для инерционных рв

Для безынерционного РВ величина предельной дальности R_д является одновременно максимальной дальностью R_д= R_{д макс} , так как разрыв снаряда происходит мгновенно при наличии соответствующего сигнала от цели. При инерционном взрывателе произойдет смещение точки подрыва РВ от R_макс , так как действие РВ в этом случае определяется не только уровнем, но и длительностью сигнала.

Величину предельной дальности, отвечающую инерционному взрывателю, обозначим через R_ди . Очевидно, что

Методика расчета предельной дальности, у инерционных РВ сводится к следующему.

1.Определяется предельная дальность R_{д макс}, которая получается в том случае, если не учитывать условий стрельбы (углы встречи), частотной и временной характеристик РВ и сдвига максимума диаграммы излучения

При этом под U понимается наибольшая чувствительность тракта низкой частоты. Величина DF²=G и должна выбираться из условия F= 1. Тогда

2.Определяется предельная дальность R_{д макс}, которая была бы у безынерционного РВ с учетом условий стрельбы, но без учета временной характеристики РВ. С этой целью строится диаграмма срабатывания R_д(γ)= R_макс (γ). Из полученной диаграммы находится нормированное значение дальности R _макс и затем его абсолютное значение

3.Чаще всего инерционность РВ оценивается не по време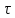ни ,а по расстоянию (посредством счёта импульсов). Нужное количество символов , необходимых для срабатывания РВ , переводится в соответствующую инерционность по времени , а затем рассчитывается дальность подрыва R_{д макс} . Пусть РВ срабатывает после поступления на вход счётчика n импульсов , т.е n амплитудных значений сигнала какой-либо одной полярности , или , что то же самое , по истечении n переходов колебания доплеровской частоты F_д.

Тогда, если полагать, что при γ = 90

(5.24)

длительность периода колебаний допплеровской частоты составляет (в среднем)

(5.25)

Инерционность РВ по времени

(5.26)

Координата х_д в случае безынерционного РВ соответствует х_т и находится из соотношения

,

где

(5.27)

Величина х_дн инерционных РВ определяется из следующих соображений. При инерционности по времени , заменяя реальный сигнал (рисунок 5.18) идеальным, в виде прямоугольника и считая, что точки R_m и х_т соответствуют середине сигнала, т. е. задержка момента срабатывания РВ относительно точки

R_макс определяется величиной, найдем координату

, (5.28)

Рисунок 5.18

В случае РВ с инерционностью по расстоянию определяем период Т_д, инерционность и затем протяженность участка траектории , в пределах которого на предельном промахе реализуется n периодов Т_д

; (5.29)

. (5.30)