
- •3) Типовые постановки задач системного анализа
- •4) Переходные процессы и переходные функции.
- •5)Элементарные звенья систем и дифференциальные уравнения, описывающих их работу.
- •6) Основные требования к моделям в теории систем.
- •7) Типы шкал, используемых в теории систем. Примеры их применения.
- •8) Принцип положительной и отрицательной обратной связи. Примеры.
- •9)Определение цели. Виды и формы представления структур целей.
- •10) Построение дерева целей и проблем.
- •11) Модель межотраслевого баланса в теории систем.
- •12) Линейное программирование в решении задач системного анализа.
- •13) Системы массового обслуживания, примеры Теория массового обслуживания
- •Классификация смо и их основные элементы
- •14)Использование временных рядов.
- •15) Статистические методы при решении задач экономического содержания.
- •16)Метод организации сложных экспертиз.
- •17) Математические методы экспертных оценок.
- •18) Коэффициент ранговой корреляции Спирмена и Кендалла. Их применение.
- •19)Оптимизационные задачи на применение множителя Лагранжа.
- •Описание метода
- •Обоснование
- •Двумерный случай
- •Применение
4) Переходные процессы и переходные функции.
5)Элементарные звенья систем и дифференциальные уравнения, описывающих их работу.
При исследовании динамики систем часто невозможно составить математическое описание всей системы сразу. Для облегчения этой задачи систему разбивают на отдельные элементы и для каждого из них составляют дифференциальные уравнения. Для отображения динамических свойств элементов системы независимо от их физической природы используют понятие динамического звена. Динамическое звено - это часть системы или элемента, описываемая определенным дифференциальным уравнением. Динамическим звеном можно представить элемент, совокупность эле-ментов, автоматическую систему в целом. Любую динамическую систему можно условно разложить на динамические «атомы» - элементарные динамические звенья.
Элементарное звено должно быть звеном направленного действия: звено передает воздействие только в одном направлении с входа на выход, так что изменение состояния звена не влияет на состояние предшествующего звена, работающего на вход.
Дифференциальные
уравнения элементов имеют порядок не
выше второго, поэтому типовые звенья
описываются дифференциальными уравнениями
нулевого, первого и второго порядка.
Таким образом, разновидностей элементарных
динамических звеньев немного.
Все
звенья различают по виду уравнений,
определяющих характеристики переходных
процессов, возникающих в них при
одинаковых исходных условиях и одинаковом
виде возмущения.
Для оценивания
поведения элементарного звена обычно
на его вход подают тестовые сигналы
определенной формы. Наиболее часто
используются такие виды возмущающих
сигналов.
1. Ступенчатое воздействие
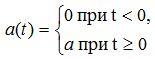 Частым
случаем ступенчатого воздействия
является единичное воздействие, которое
описывается так называемой единичной
функцией
Частым
случаем ступенчатого воздействия
является единичное воздействие, которое
описывается так называемой единичной
функцией
 2.
Импульсное воздействие (единичный
импульс или дельта функция) x(t) = σ(t) (рис.
3,б):
2.
Импульсное воздействие (единичный
импульс или дельта функция) x(t) = σ(t) (рис.
3,б):
 3.
Периодический сигнал: либо в виде
синусоиды, либо в виде прямоугольной
волны.
5. Виды типовых звеньев и их
переходные функции
Воздействие на
вход системы вызывает изменение ее
выхода y(t) - переходный процесс, именуемый
переходной функцией.
Переходная
(временная) функция — это реакция
выходной переменной звена на изменение
входа.
3.
Периодический сигнал: либо в виде
синусоиды, либо в виде прямоугольной
волны.
5. Виды типовых звеньев и их
переходные функции
Воздействие на
вход системы вызывает изменение ее
выхода y(t) - переходный процесс, именуемый
переходной функцией.
Переходная
(временная) функция — это реакция
выходной переменной звена на изменение
входа.
Все динамические звенья могут быть описаны сл. элементарными звеньями:
Безынерционное звено
описывается уравнением:
y(t) = kx(t),
где k — коэффициент пропорциональности или усиления (здесь и во всех последующих уравнениях.
 2)Инерционное
звено (апериодическое)
2)Инерционное
звено (апериодическое)
описывается
дифференциальным уравнением:
![]() где
Т — постоянная времени, определяемая
емкостью звена и его пропускной
способностью.
3)Дифференцирующее
звено.
где
Т — постоянная времени, определяемая
емкостью звена и его пропускной
способностью.
3)Дифференцирующее
звено.
описывается дифференциальным уравнением: y(t) = kx'(t)
Реальное дифференцирующее звено описывается дифференциальным уравнением
![]() 4)Интегрирующее
звено
4)Интегрирующее
звено
писывается дифференциальным уравнением
y’(t) = kx(t).
5)Колебательное звено
в общем виде
описывается следующим уравнением:
![]() 6)Звено
чистого запаздывания
6)Звено
чистого запаздывания
повторяет по форме входной сигнал, но с запаздыванием по времени y(t) = kx(t - τ),
где τ - время запаздывания.
