
- •Терминология Математический анализ
- •1. Множества, операции над ними
- •2.Числовые множества, их границы.
- •3. Операции над символами бесконечности
- •4. Понятие функции
- •5. Частные классы отображений
- •6.Класс основных элементарных функций.
- •7. Суперпозиция (композиция отображений)
- •8. Системы окрестностей
- •9. Предел последовательности (определение Коши)
- •14. Классификация точек разрыва
- •15. Замечательные пределы.
- •16. Второй замечательный предел и его свойства.
- •18. Главная часть б.М.
- •19. Сравнение б.М.
- •20. Сравнение б.Б.
- •21. Свойства эквивалентных бесконечно малых функций.
- •22. Таблица эквивалентных б.М.
- •23. Понятие производной.
- •24. Физический, геометрический и экономический смысл производной.
- •25. Таблица производных.
- •26. Производная сложных функций.
- •31. Уравнение касательной плоскости и нормали к поверхности.
- •33. Формула Тейлора.
- •37. Условия постоянства функции.
- •38. Достаточные условия экстремума.
- •39. Выпуклость графика функции.
- •40. Асимптоты графикафункции.
- •41. Общая схема исследования функции
- •I этап – асимптотическое исследование фун-и
- •II этап – исследование фун-и на монотонность.
- •42. Формулы
9. Предел последовательности (определение Коши)
Пределом последовательности Xn называют число А, если для любого сколько угодно малого е >0 существует N (е) такой, начиная с которого (n>N) выполняется неравенство |xn-А|< е
![]()
Предел векторной последовательности {yn} – вектор (точка) А (принадлежащая пространству Rn), при которой для любой окрестности U существует окрестность V такая, что для всех n, (принадлежащих окрестности V) последовательность yn принадлежит (U).
Теорема1. Для того, чтобы последовательность
![]() точек
(векторов) пространства Rk
сходилась к точке (вектору) А=(А1,
А2,
…Аk),
чтобы каждая координатная последовательность
точек
(векторов) пространства Rk
сходилась к точке (вектору) А=(А1,
А2,
…Аk),
чтобы каждая координатная последовательность
![]() сходилась
и при этом
сходилась
и при этом![]() (
(![]() ).
).
Теорема2. Всякая монотонно возрастающая (убывающая) и ограниченная сверху (снизу) числовая последовательность имеет предел.
Теорема3.
Если даны три числовых последовательности
un,vn,bn,
удовлетворяющие условию un
bn
vn
и
![]()
![]() , то и
, то и
lim wn=A.
![]()
10.Определение предела функции на языке последовательностей (определение Гейне).
Говорят, что точка А – предел функции f(x)
![]() ,
если для всякой последовательности
точек {xn}
(xnx0)
из области определения функции, сходящейся
к х0,
последовательность {f(xn)}
значений функции имеет пределом точку
А.
,
если для всякой последовательности
точек {xn}
(xnx0)
из области определения функции, сходящейся
к х0,
последовательность {f(xn)}
значений функции имеет пределом точку
А.
11. Теоремы о пределах.
1. Если предел существует, то он единственный, если пределов больше 1, то предела не существует.
2. Если существует предел Xn=a, то ограничена в окрестности точки а. (обратное нет!)
3. Всякая монотонная ограниченная последовательность имеет предел.
4.
Пусть
![]() ,
,
![]() ,
тогда А – предел суммы:
,
тогда А – предел суммы:

Предел вычисляется, если yn0, предел =0, а yn0.
12. Раскрытие неопределенности.
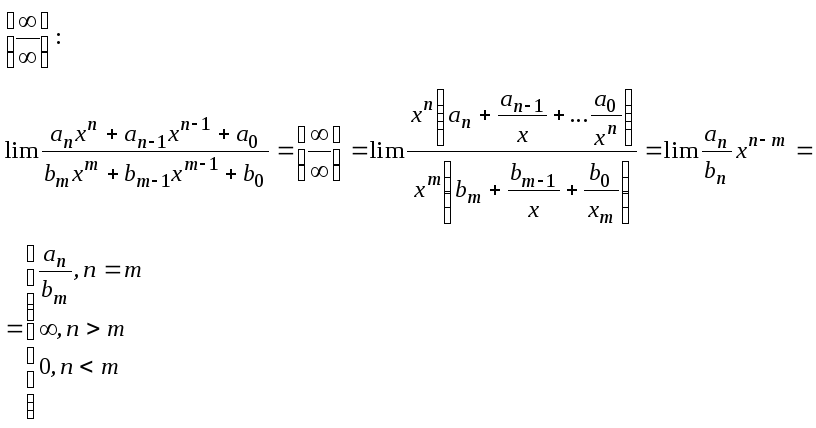
![]()
Чтобы решить пример с данной неопределенностью, необходимо максимально упростить выражение, сократить какие-либо переменные, и подставить число из предела.
![]()
Чтобы
решить пример с этой неопределенностью,
мы упрощаем выражение и затем подставляем
![]() вместо неизвестной переменной. По
определенным формулам ищем значение.
вместо неизвестной переменной. По
определенным формулам ищем значение.
![]()
13. Непрерывность функций.
Непрерывной называется функция f(x) в точке x0, если предел f(x)=f(x0) при хх0.
lim f(x)=f(x0)lim f(x)=lim f(x)=f(x0)
xx0 xx0
lim (x0-0)=lim f(x) - предел слева
lim (x0+0)=lim f(x) – предел справа.
Непрерывной является такая функция, у которой предел слева = пределу справа.
Теорема1. Для того, чтобы функция была непрерывной в точке х0 чтобы она была непрерывна слева и справа в этой точке.
Теорема2. Если функции f и t непрерывны в точке х0, то и функции f+t, f*t, f/t (t(x0)0) тоже будут непрерывны в этой точке.
Теорема3. Для того, чтобы функция y = f(x) была непрерывна в точке х0, чтобы все ее координатные функции были непрерывны в х0.
Теорема4.
Пусть функция f
непрерывна в точке x0
и t
непрерывна в точке y0.
Тогда их суперпозиция (сложная функция)
f![]() t=f(t)
также непрерывна в точке х0.
t=f(t)
также непрерывна в точке х0.
Теорема5. Все элементарные функции вещественного переменного непрерывны в области определения.
Теорема6. Пусть скалярная функция f скалярного переменного задана на отрезке [a,b] и f(a)=A, f(b)=B, AB. Если функция f непрерывна на [a,b], то для любого С, лежащего между А и В, существует точка с [a,b] такая, что f(c)=C.
Теорема7. Если функция y=f(x) непрерывна в замкнутой области Х и в некоторых точках, принадлежащих этой области, принимает определенные значения, неравные между собой, то для любого числа С, заключенного между этими значениями, существует точка х2 такая, что f(x2)=C.
Теорема 8 (I теорема Вейерштрасса). Всякая непрерывная на замкнутом ограниченном в Rn множестве Х функция y=f(x) ограничена на этом множестве.
Теорема9 (II теорема Вейерштрасса). Всякая непрерывная на замкнутом ограниченном множестве в Rn функция f(x) принимает в нем наибольшее и наименьшее значения.
Степенная функция – функция вида f(x) = x, R
Показательная функция – функция вида f(x) = ax, а1, а>0. а – const, x – переменная.
Степенно-показательная функция – функция вида f(x)=u(x)v(x).
Точка разрыва функции f(x) - точка х0 в которой нарушается непрерывность, а поэтому в этой точке нарушается одно из равенств.
