Терминология Математический анализ

1. Множества, операции над ними

Заданное множество – такое множество, при котором есть правило, позволяющее установить относительно любого объекта, является ли он элементом этого множества или нет.

Множество А входит в В (А – подмножество В), если для любого а А соответствует аВ.

Множ-ва называют равными, если АВ и ВА.

Расширенное множество вещественных чисел –множество |R=|R+(), где - несобственные числа.

Операции над множествами.

Объединение или сумма множеств А и В – множество С, состоящее из всех элементов множеств А и В (АВ, А +В) не содержит других элементов.

Свойства множеств:

АА=А, АВ=ВА,

(АВ) С = А(ВС)

Пересечение множеств А и В – Множество С (С=АВ), состоящее лишь из тех элементов, которые принадлежат одновременно А и В.

Свойства множеств:

АВ=ВА, АА=А

(АВ) С=А(ВС)

Разность множеств А и В – множество А\В, содержащее все те и только те элементы множества А, которые не являются элементами множества В.

Прямое (декартовое) произведение множеств А и В – множество А×В, элементами которого являются всевозможные пары (а,в), где аА, в В.

2.Числовые множества, их границы.

Вещественное (действительное) число – любая десятичная дробь.

N – натуральные числа 1, 2…;

Z – все целые числа

Q – рациональные числа (периодические десятичные дроби)

Сегмент (отрезок, замкнутый промежуток) – множество х чисел, удовлетворяющих неравенству a  x  b, обозначается [a,b].

Интервал (открытое множество) – множество х чисел, удовлетворяющих неравенству a < x < b, обозначается (а, b); если a  x <b, то это полуинтервал [a,b).

Верхней границей множ-ва АR называют такое число с R, если для всякого а А выполнено неравенство а  с.

3. Операции над символами бесконечности

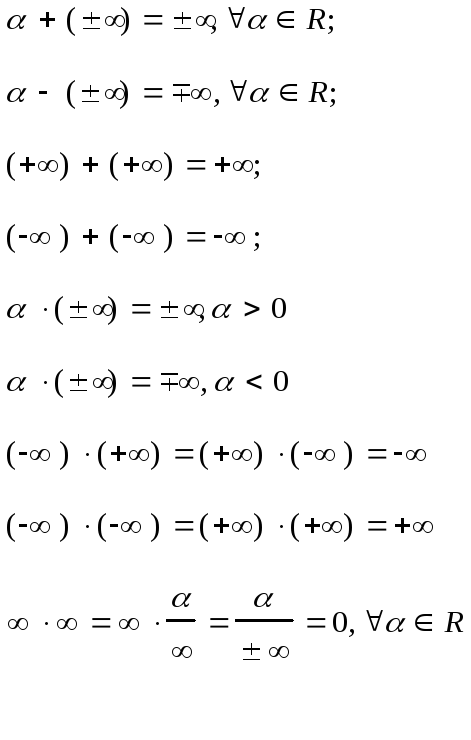
Неопределенными называются такие операции, как

Множество А называется ограниченным сверху, если x<b.

Множество А называется ограниченным снизу, если x>b.

Множество А называется ограниченным, если оно ограничено и сверху, и снизу.

Точная верхняя граница (супремум, supA) –наименьшая из всех верхних границ.

Точная нижняя граница (инфимум, infA) – наибольшая из всех нижних границ.

Свойства модуля |x|:

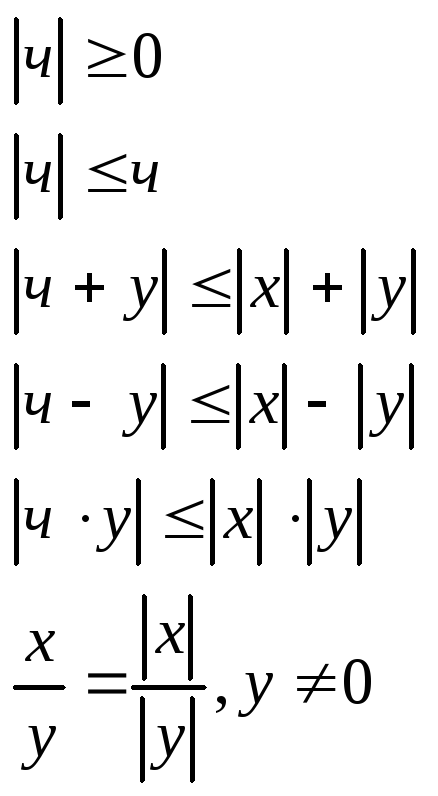
4. Понятие функции

Пусть даны два множества X и Y. Говорят, что задано отображение множеств X а во множество Y (или задана функция на Х со значениями в Y), если всякому x X по некоторому правилу f поставлен в соответствие элемент y Y.

f : X Y, x y

При этом элемент y = f(x) называют образом элемента х при отображении f.

Многозначная функция – много значений у.

Однозначная функция – одно значение у.

х – аргумент (прообраз)

у – значение функции (образ).

Функция взаимнооднозначная – если каждому значению х соответствует значение у.

Числовая последовательность – функция натурального аргумента f(n) или f:NR.

Способы задания функции:

Явный способ – можно выразить переменную.

Неявный способ – нельзя выразить переменную.

Параметрический – каждая функция выражается через параметр.

Графический.

Табличный.

Алгоритмический.