18 Осевая деформация прямолинейного стержня : Внутренние силы и напряжения,эпюры

Под растяжением (сжатием) понимают такой вид нагружения, при котором в поперечных сечениях стержня возникают только нормальные силы, а прочие силовые факторы равны нулю.Рассмотрим однородный прямолинейный стержень длиной l и площадью поперечного сечения F, на двух концах которого приложены две равные по величине и противоположно направленные центральные продольные силы Р (рис. 2.1, а). Поместим начало плоской системы координат yz в центре тяжести левого сечения, а ось z направим вдоль продольной оси стержня. Для определения величин внутренних усилий воспользуемся методом сечений. Задавая некоторое сечение на расстояние z (0 £ z £ l) от начала системы координат и рассматривая равновесие левой относительно заданного сечения части стержня (рис. 2.1, б), приходим к следующему уравнению: P + Nz = 0,откуда следует, что Nz = P = const. Примем для Nz следующее правило знаков. Если Nz направлена от сечения, т.е. вызывает положительную деформацию (растяжение), то она считается положительной. В обратном случае - отрицательной.

Рис. 2.1

Нормальная сила Nz приложена в центре тяжести сечения, является равнодействующей внутренних сил в сечении и, в соответствии с этим, определяется следующим образом:

Но из этой формулы нельзя найти закон распределения нормальных s напряжений в поперечных сечениях стержня. Для этого обратимся к анализу характера его деформирования.

Если на боковую поверхность этого стержня нанести прямоугольную сетку (рис. 2.1, б), то после нагружения поперечные линии а-а, b-b и т.д. переместятся параллельно самим себе, откуда следует, что все поверхностные продольные волокна удлинятся одинаково. Если предположить также, что и внутренние волокна работают таким же образом, то можно сделать вывод о том, что поперечные сечения в центрально растянутом стержне смещаются параллельно начальным положениям, что соответствует гипотезе плоских сечений, введенной швейцарским ученым Д. Бернулли, гласящей, что плоские сечения до деформации остаются плоскими и после деформации. Значит, все продольные волокна стержня находятся в одинаковых условиях, а следовательно, нормальные напряжения во всех точках поперечного сечения должны быть также одинаковы и равны , где F - площадь поперечного сечения стержня.Высказанное предположение о равномерном распределении внутренних сил в попер сечении справедливо для участков, достаточно удаленных от мест: резкого изменения площади попер сечения (рис. 2.1, в); скачкообразного изменения внешних нагрузок; скачкообразного изменения физико-механ характ-ик конструкций. Основанием для такого утверждения служит принцип Сен-Венана, справедливый для любого типа напряженного состояния и формулируемый следующим образом: особенности приложения внешних нагрузок проявляются на расстояниях, не превышающих характерных размеров поперечного сечения стержня.Эпюрами прод сил и норм напряжений назыв графики, показыв законы изменения сил и напряжений в попер сечениях по длине стержня.

19 Концентрация напряжений, концентраторы, коэффициенты напряжений концентрации - в теории упругости - положение, согласно которому уравновешенная система сил, приложенных к какой-либо части твердого тела, вызывает в нем напряжения, быстро убывающие по мере удаления от этой части, и может быть заменена эквивалентной системой сил. Сформулирован А. Сен-Венаном в 1855.Концентрация напряжений Вблизи различного рода отверстий, надрезов, выточек и, вообще,(мест резкого изменения поперечных размеров распределение напряжений становится существенно неравномерным, и возникают зоны повышенных напряжений. Например, при одноосном равномерном растяжении напряжениями σ тонкой пластинки шириной Н с небольшим (d<Н/5) круглым отверстием распределение напряжений по поперечному сечению, проходящему через центр отверстия, оказывается существенно неравномерным с пиками напряжений в точках А и В контура отверстия (4.21). Точное решение показывает, что нормальные напряжения в радиальных сечениях на контуре отверстия изменяются по закону σθ=σ(1-2cos2θ) и в точках А и В при θ=π/2 достигают величины σmax=3σ, а при θ=0, т. е. в сечении, параллельном линии действия нагрузки, действуют сжимающие напряжения σθ=σ, равные по величине приложенным к пластинке напряжениям.

Рис. 4.21. Концентрация напряжений в пластине с отверстием Неравномерность распределения напряжений по поперечному сечению имеет место и при центральном растяжении ступенчатого бруса (4.22), причем максимальные напряжения быстро увеличиваются по мере уменьшения радиуса закругления переходной части (галтели). Большие местные напряжения возникают также в зоне контакта деталей (контактные напряжения).

Явление возникновения значительных местных напряжений называется концентрацией напряжений, а причина, вызвавшая концентрацию - концентратором напряжений. Концентрация напряжений характеризуется коэффициентом концентрации α. Величину α также называют теоретическим коэффициентом концентрации. Коэффициентом концентрации α называется отношение действительного напряжения σmax в наиболее напряженной точке к номинальному напряжению σn в той же точке, т. е.или 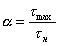. Номинальными называются напряжения, вычисленные по формулам сопротивления материалов, не учитывающим явление концентрации напряжений. В тех случаях, когда возникают трудности в вычислении номинальных напряжений в сечении с концентратором напряжений, за номинальные принимают напряжения в неослабленном сечении детали. В настоящее время методами теории упругости и экспериментальными методами (обычно путем испытания образцов из оптически активного материала в поляризованном свете) определены величины коэффициентов концентрации для многих практически важных случаев. Расчетные формулы, таблицы и графики для определения коэффициентов концентрации приводятся в справочной литературе. На Рис. 4.22 представлен характер зависимости коэффициента концентрации от отношения радиуса галтели ρ к диаметру d в случае осевого растяжения ступенчатого бруса.

Рис. 4.22. Концентрация напряжений для галтельного соединенияКонцентраторы напряжений – местные резкие изменения однородности (формы и, следовательно, жесткости) конструкции, приводящие к резкому местному (локальному) повышению напряжений в конструкции. На рисунке показано действие растягивающей внешней нагрузки, равномерно распределенной по краям простейших конструктивных элементов – листов. Пунктирные линии представляют собой так называемые траектории напряжений, вдоль которых напряжение передается от молекулы к молекуле. Для гладкого листа эти линии параллельны, напряжения в любом сечении листа одинаковы.

Силы, передающиеся по траекториям напряжений в листах с концентраторами (надрез в кромке листа, отверстие в центре листа), обходят разрыв в материале. Плотность траекторий напряжений увеличивается, и локальные напряжения у края концентратора возрастают (иногда многократно). В этих местах может произойти нарушение (разрыв) межатомных связей, возникнут микротрещины, распространение которых ведет к разрушению конструкции.