40. Интеграл от фкп.

Пусть задана непрерывная функция f(z)=u(x,y)+iv(x,y) на гладкой дуге L=AB , соединяющей точки z₀ иz, тогда .

Интегралы, стоящие в правой части равенства являются криволинейными интегралами по координатам (второго рода). Эти интегралы удобнее всего считать, если уравнение дуги АВ задано параметрически, причем значение параметра в точке A=t₁, а значение параметра в точке B=t₂. Тогда интеграл от ФКП вычисляется по формуле .

Если f(z) аналитическая функция в области D, а АВ гладкая дуга, лежащая в этой области, то вычисление интеграла от ФКП можно производить по формуле Ньютона-Лейбница. Формулы для нахождения первообразной для аналитической функции являются обычными формулами интегрирования .

39.Аналитические функции в области и в точке.

Функция W=f(z) называется аналитической в области D, если она дифференцируема в каждой точке этой области. Функция W=f(z) называется аналитической в точке z0, где 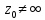, если она аналитична в некоторой окрестности точки z0. Аналитические функции также называют регулярными или моногенными. Понятие дифференцируемости и аналитичности функции в области совпадают, а в точке нет. Требования аналитичности более жесткие. Все точки, в которых функция аналитическая, называют правильными точками f(z). Точки, в которых функция не аналитическая, называют особыми точками. Элементарные функции являются аналитическими во всей области своего определения и для них справедливы все формулы дифференцирования. Если известны только действительная или только мнимая части аналитической функции, то эта функция может быть полностью восстановлена по известной части с точностью до константы.

38. Производная фкп. Необходимое и достаточное условия дифференцируемости фкп в точке (условия Коши-Римана).

Производная функции w=f(z) называется .

Если функция имеет производную в точке z0, то она называется дифференцируемой в точке z0. Для дифференцируемой функции W=f(z)=u(x,y)+iv(x,y) в данной точке необходимо и достаточно, чтобы функции u и v были дифференцируемы в данной точке и чтобы в этой точке выполнялись условия Коши-Римана (C-R).

.

.

Если эти условия выполнены для функции f(z), то производную можно посчитать по одной из формул:.

37. Основные функции комплексного переменного.

Если на множестве М точек плоскости z задана функция w=f(z), то это означает, что указан закон, по которому каждой точке zϵM ставится в соответствие определенная точка или множество точек W. Если ставится одна точка, то функция называется однозначной, а если больше двух, то – многозначной. Если z=x+iy, а w=u+iv, то задание функции f(z)=w будет равносильно заданию двух функций действительного переменного u=u(x,y), v=v(x,y), f(z)=u(x,y)+iv(x,y).

Элементарные функции комплексного переменного определяются как суммы рядов, сходящихся на всей комплексной площади.

А действительной оси эти функции совпадают с соответствующими элементарными функциями действительного переменного. Для функции комплексного переменного справедлива формула Эйлера:.

Из это формулы следует, что:

1..

2..

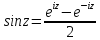Следствия:

а..

б..

в.

г..

3..

4.

5.

6.

7.

.

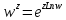Условимся откладывать значение z на одной комплексной плоскости, а значение w=f(z) на другой. Назовем эту плоскость w, а ее оси u и v.

Если при отображении множества М на плоскости z получается множество N на плоскости w и при этом двум различны точкам из М соответствует две различных точки из N, то такое отображение называется однозначным или однолистным.