5.Критерии подобия и критериальные уравнения.

Кри­терия подобия- числа подобия, составленные из заданных параметров математического описания процесса. Помимо безразмерных величин и безразмерных координат в уравнения входят также безразмерные комплексы . 1)Число Нуссельта безразмерным коэффициентом теплоотдачи,который характеризует теплообмен на границе стенка – жидкость. ,где -коф. теплоотдачи,а -теплопроводности. 2)Число Рейнольдса характеризует соотношение сил инерции и сил вязкости. .3)Число Пекле , можно преобразовать, где числитель характеризует теплоту, переносимую конвекцией, а знаменатель – теплоту, переносимую теплопроводностью.

4)Число Грасгофа характеризует подъемную силу, возникающую в жидкости вследствие из-за плотностей. 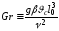. -коэф. температурного расширения

5) число Архимеда ,где -плотность.

К независимым переменным относятся координаты X, У; К зависимым переменным –Nu, Θ, W_x, W_y; И к постоянным величинам – это Ре, Re, Gr;

уравнения подо­бия

; ;

6) число Эйлера характеризует соотношение сил давления и сил инерции .7) число Прандтля является физи­ческим

параметром. 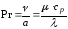Уравнение энергии 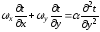и уравнение движения .

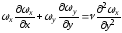Числа Pr капельных жидкостей сильно зависят от температуры,а для газов не зависит ни от температуры, ни от давления и является величиной постоянной, определяемой атомностью газа. Уравнения подобия можно записать в виде

; ;

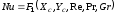. Безразмер­ные переменные делятся на :

– определяемые – это числа, в которые входят зависи­мые переменные; в нашем случае это , следовательно, определяемыми являются Nu, Θ, W_x и W_y;

– определяющие – это числа, полностью составленные из незави­симых переменных и постоянных величин,которые входят в условия однознач­ности; это X, У, Re, Pr (или Ре) и Gr.

6.Условия подобия физических процессов.

Аналогичные явления - явления природы, которые описываются оди­наковыми по форме записи дифференциальными уравнениями, но раз­ными по физическому содержанию.Подобные процессы – процессы, которые удовлетворяют общим условиям подобия физических процессов. Условия подобия физических процессов:

1) Условия однозначности подобных процессов должны быть оди-наковыми во всем, кроме числовых значений размерных постоянных, содержащихся в этих условиях .

2) Подобные процессы должны быть качественно одинаковыми, т. е. они должны иметь одинаковую физическую природу и описываться одинаковыми по форме записи дифференциальными уравнениями. Это условие говорит, что подобные процессы должны относиться к одному и тому же классу физических явлений. Помимо одинаковой, физической природы подобные процессы должны характеризоваться одинаковыми по записи дифференциальными уравнениями. Из этих условий следует, что подобные процессы должны описываться одинаковыми дифференциальными уравнениями и граничными условиями. Следовательно, процессы описываются единой формулой, например

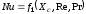
3) Одноименные определяющие безразмерные переменные подобных процессов должны иметь одинаковое числовое значение.