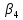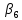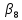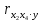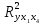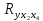МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ

ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ

ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ

ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ

«УДМУРТСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ»

ИНСТИТУТ ЭКОНОМИКИ И УПРАВЛЕНИЯ

КАФЕДРА МАТЕМАТИЧЕСКИХ МЕТОДОВ В ЭКОНОМИКЕ

Лабораторная работа

на тему: «Множественная регрессия»

по дисциплине «Эконометрика»

Вариант 9

Выполнил студент гр. 061800-31	Нуриева Г. Р.
Проверил Ассистент кафедры «Математических методов экономике»	Неустроев Г.В.

Ижевск, 2011 г.

Содержание

Постановка задачи 3

Решение задачи 4

Вывод 10

Приложение 1 12

Приложение 2 18

Постановка задачи

Изучается зависимость по 79 административно-территориальным единицам фактического конечного потребления домашних хозяйств y_t от следующих параметров:

• среднедушевых доходов населения,

• ВРП на душу населения,

• основных фондов организаций на душу населения,

• средний размер банковского вклада физ. лиц,

• сальдированный финансовый результат на душу населения,

• инвестиции в основной капитал на душу населения,

• индексы потребительских цен,

• сальдо внешнеторгового баланса на душу населения.

Исходные данные представлены в приложении 1.

1. Вычислить описательные статистики.

2. Построить матрицу парных коэффициентов корреляций. Установить какие факторы коллинеарны.

3. Построить уравнение множественной регрессии в нормальном и стандартизованном масштабе, включив в модель все факторы.

4. Рассчитать средний коэффициент эластичности.

5. Определить частные и множественные коэффициенты корреляции.

6. Оценить статистическую значимость уравнения множественной регрессии с помощью критериев Стьюдента и Фишера. Определить какие факторы значимо воздействуют на формирование зависимого фактора в этом уравнении.

Решение задачи

1. Вычисление описательных характеристик.

Обозначим все переменные как y и x. Пусть

• фактическое конечное потребление домашних хозяйств обозначается как y_t,

• среднедушевых доходов населения x_1t,

• ВРП на душу населения x_2t,

• основных фондов организаций на душу населения x_3t,

• средний размер банковского вклада физ. лиц x_4t,

• сальдированный финансовый результат на душу населения x_5t,

• инвестиции в основной капитал на душу населения x_6t,

• индексы потребительских цен x_7t,

• сальдо внешнеторгового баланса на душу населения x_8t.

К ним относятся математическое ожидание и среднеквадратическое отклонение переменных. Найдем оценки математического ожидания, как:

В итоге получаем следующие результаты:

yt	x1t	x2t	x3t	x4t	x5t	x6t	x7t	x8t
42107,11	4338,65	63450,82	212096,31	2434,97	5038,47	14974,22	112,71	351,27

Оценки дисперсий определяются по следующим формулам:

436695254,80	5709704,53	2385412200,80	16860444377,65	1022085,85	116356921,95	463280089,36	4,51	758405,26

Таким образом, оценка среднеквадратического отклонения равна:

20897,25	2389,50	48840,68	129847,77	1010,98	10786,89	21523,94	2,12	870,86

2. Построение матрицы парных коэффициентов корреляций.

Расчет матрицы парных корреляций произведем по формулам:

В результате получаем следующую матрицу парных коэффициентов корреляции, представленные в таблице ниже.

r	yt	x1t	x2t	x3t	x4t	x5t	x6t	x7t	x8t
yt	1,0000	0,9726	0,8004	0,5186	0,9042	0,7340	0,5782	0,0754	0,3273
x1t	0,9726	1,0000	0,8806	0,6128	0,8825	0,7356	0,6924	0,0979	0,3951
x2t	0,8004	0,8806	1,0000	0,8472	0,7392	0,7808	0,8423	0,0952	0,6711
x3t	0,5186	0,6128	0,8472	1,0000	0,5057	0,5707	0,6154	0,0646	0,8128
x4t	0,9042	0,8825	0,7392	0,5057	1,0000	0,7320	0,4955	0,1393	0,2981
x5t	0,7340	0,7356	0,7808	0,5707	0,7320	1,0000	0,5273	0,0190	0,5884
x6t	0,5782	0,6924	0,8423	0,6154	0,4955	0,5273	1,0000	0,1670	0,4306
x7t	0,0754	0,0979	0,0952	0,0646	0,1393	0,0190	0,1670	1,0000	-0,0895
x8t	0,3273	0,3951	0,6711	0,8128	0,2981	0,5884	0,4306	-0,0895	1,0000

Можно сделать вывод о том, что между экзогенными переменными x₁, x₂, x₃, x₄ существует корреляционная связь, что может привести к появлению мультиколлинеарности, что может сказаться на качестве модели прогнозов, сделанных по полученной модели.

3. Построение уравнения множественной регрессии в нормальном и стандартизованном масштабе.

Рассчитаем параметры эконометрической модели множественной регрессии в стандартизованном масштабе: где — стандартизованные переменные: для которых среднее значение равно нулю, а среднее квадратическое отклонение равно единице; 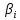— стандартизованные коэффициенты регрессии. Стандартизованные значения приведены в приложении 2.

Оценки стандартизованных коэффициентов будут равны:

1,0220	-0,1142	-0,0654	0,1167	0,0572	-0,0889	-0,0100	0,0223

Оставим наиболее значимые оценки, то есть , и . Можно сделать вывод о том, что среднедушевые доходы населения, ВРП на душу населения и средний размер банковского вклада физ. лиц имеют более значимую связь для фактического конечного потребления домашних хозяйств. Так как стандартизованные коэффициенты регрессии можно сравнивать между собой, то можно сказать о том, что среднедушевые доходы населения влияют гораздо больше, чем другие факторы.

Таким образом, после преобразования получаем уравнение:

С учетом выброса пересчитаем оценки стандартизованных коэффициентов. Они будут равны соответственно 1,0184; -0,2214 и 0,1690.

Зная стандартизованные коэффициенты, находим уравнение регрессии в нормальном масштабе. Оценки коэффициентов в нормальном и стандартизованном масштабах связаны между собой следующими соотношениями:

.

Тогда, . Свободный член определяется по формуле . То есть .

Следовательно,

.

4. Расчет среднего коэффициента эластичности.

Сравнивать влияние факторов на результат можно также при помощи средних коэффициентов эластичности:

.

Вычисляя, получаем

То есть увеличение только среднедушевых доходов населения (от своего среднего значения) или только среднего размера банковского вклада физ. лиц на 1% увеличивает в среднем фактическое конечное потребление домашних хозяйств на 0,9177% и 0,0855% соответственно. Однако, увеличение ВРП на душу населения на 1% снижает в среднем фактическое конечное потребление домашних хозяйств на 2,9174%.

5. Определение частных и множественных коэффициентов корреляции.

Частные коэффициенты корреляции характеризуют тесноту связи между результатом и соответствующим фактором при элиминировании (устранении влияния) других факторов, включенных в уравнение регрессии.

Показатели частной корреляции представляют собой отношение сокращения остаточной дисперсии за счет дополнительного включения в анализ нового фактора к остаточной дисперсии, имевшей место до введения его в модель.

Найдем частные коэффициенты корреляции по формулам:

Получаем:

0,2117	0,1923	0,2082	-0,1145	0,0927	0,3511	0,2635	0,0057	0,0111

Для последующих расчетов необходимо найти и другие частные коэффициенты корреляции. Их можно найти через матрицу парных коэффициентов корреляции по следующей формуле:

,

Где —

определитель матрицы парный коэффициентов корреляции;

— определитель матрицы межфакторной корреляции (по i-ой строчке и i‑ому столбцу).

Таким образом, получаем

0,9046	0,8182	0,9134	0,8343	0,9875	0,9751

Теперь рассчитаем совокупный коэффициент корреляции . Для этого воспользуемся формулой: . Он равен 0,983.

Из полученных результатов можно сделать вывод, что коэффициент множественной корреляции свидетельствует о тесной зависимости переменной y_t от x_1t , x_2t и x_4t, так как она равна 98,3%. Соответственно прочие факторы составляют 1,7% от общей вариации y_t.

6. Оценка статистической значимости уравнения множественной регрессии с помощью критериев Стьюдента и Фишера.

Значимость уравнения множественной регрессии в целом, так же как и в парной регрессии, оценивается с помощью F-критерия Фишера:

где R² — совокупный коэффициент корреляции, Т — число наблюдений, n — количество параметров в модели. Для нашей модели получаем:

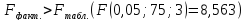, поэтому можно сделать вывод о том, что с вероятностью 0,95 уравнение, сформированное под неслучайным воздействием факторов x_1t , x_2t и x_4t, признается статистически значимым в целом. Частный F-критерий оценивает значимость коэффициентов чистой регрессии.

Таким образом, для представленной модели коэффициенты будут равны и .

, следовательно, сравнивая полученные значения, приходим к выводу о целесообразности включения в модель факторов x_2t и x_4t и нецелесообразности включения фактора x_1t.

Зная величины можно определить t-критерий для коэффициентов регрессии при i-ом факторе по формуле: . В результате получаем 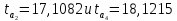. Оценки 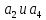являются статистически значимыми, так как (: t(0,05;75) = 1,9921). Оценка же не является статистически значимой.

Вывод

В данной работе была определена регрессия по 79 административно-территориальным единицам фактического конечного потребления домашних хозяйств на следующие параметры:

• среднедушевые доходы населения,

• ВРП на душу населения,

• основные фонды организаций на душу населения,

• средний размер банковского вклада физ. лиц,

• сальдированный финансовый результат на душу населения,

• инвестиции в основной капитал на душу населения,

• индексы потребительских цен,

• сальдо внешнеторгового баланса на душу населения.

При построении матрицы парных коэффициентов корреляции было выявлено наличие тесной связи между некоторыми экзогенными переменными, что свидетельствует о мультиколлинеарности.

При расчете модели множественной регрессии в стандартизованном масштабе были отклонены 5 параметров:

• основные фонды организаций на душу населения,

• сальдированный финансовый результат на душу населения,

• инвестиции в основной капитал на душу населения,

• индексы потребительских цен,

• сальдо внешнеторгового баланса на душу населения.

Так как оценки стандартизованных коэффициентов были достаточны малы.

Совокупный коэффициент множественной корреляции свидетельствует о тесной зависимости переменной y_t от x_1t , x_2t и x_4t, так как она равна 98,3%. Соответственно прочие факторы составляют 1,7% от общей вариации y_t.

• При нахождении F-критерия Фишера оказалось, что построенную модель можно считать статистически значимой в целом, но частный F-критерий показал нецелесообразность включения в модель фактора среднедушевых доходов населения. Факторы: ВРП на душу населения, средний размер банковского вклада физ. лиц, наоборот, показали целесообразность включения в модель и с помощью t-критерия подтвердили свою статистическую значимость.