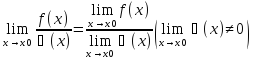- •33. Числовыми промежутками (интервалами) называют подмножества всех действительных чисел, имеющих следующий вид:
- •34. Абсолютная величина и её свойства.
- •1)Аналитический.
- •2) Графический.
- •3) Табличный .
- •36.Предел функции и его единственность. Бесконечно малые и их свойства. Связь предела с бесконечно малыми.
- •37.Неограниченные величины. Бесконечно большие и их связь с бесконечно малыми.
- •38.Предел последовательности. Ограниченность последовательности, имеющей предел. Предел монотонной функции.
- •39.Предельный переход в равенствах и неравенствах. Теорема о «двух милиционерах».
- •40. Первый замечательный предел.
- •41. Второй замечательный предел.
- •42. Пределы, связанные со вторым замечательным.
- •43. Арифметические операции над переменными, имеющими предел. Неопределенные случаи.
- •44. Непрерывность функции в точке и на промежутке. Арифметические операции над непрерывными функциями. Условия непрерывности монотонной функции и существования для ней обратной непрерывности.
- •45. Непрерывность сложной функции. Непрерывность основных элементарных и принадлежащих классу элементарных функций.
- •46. Сравнение и порядок бесконечно малых. Эквивалентные бесконечно малые и их свойства. Основные примеры эквивалентных бесконечно малых.
- •47.Сохранение знака непрерывности функции. Понятие равномерной непрерывности. Теорема Кантора (формулировка)
- •48. Теоремы Больцано-Коши (с доказательством) и Вейерштрасса (формулировки) о свойствах непрерывных на отрезке функций.
36.Предел функции и его единственность. Бесконечно малые и их свойства. Связь предела с бесконечно малыми.
Определение: Пределом функции в точке x0 называется такое число A, при котором для любого положительного ε найдется такое положительное δ, что для всех x не равных x0, удовлетворяющих неравенству |x-x0| < δ, выполняется неравенство |f(x)-A| < ε.
Геометрический смысл предела:
Если для любой ε-окрестности точки А найдется такая δ-окрестность точки x0, что для всех x неравных x0 из этой окрестности соответствующие значения функции f(x) лежат в ε-окрестности точки A.
Теорема о единственности предела:
Если предел существует, то он единственный.
Доказательство:
Пойдем от
противного. Пусть существует
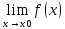 =a
и
=a
и
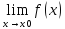 =b,
=b,
тогда
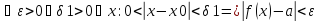
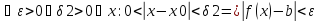
Поскольку ε – любое, то возьмем ε = |b-a|/4; и выберем δ = min{d1,d2}
Тогда
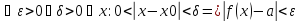
и
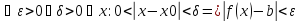
Отсюда: |b-a|=|b-f(x)+f(x)-a|=|f(x)-b|+|f(x)-a| < |b-a|/4 +|b-a|/4=|b-a|/2
|b-a|<|b-a|/2 , получили противоречие, если b неравно a, следовательно b=a
и
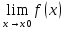 – единственный.
– единственный.
Односторонние пределы:
Число A1
называется пределом функции y=f(x)
слева в точке x0, если для
любого ε >0 существует число δ = δ(ε) >0
такое, что при x принадлежащему
(x0- δ1;x0),
выполняется неравенство |f(x)-A|<
ε. Предел слева записывают так:
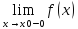 =А1
=А1
Аналогично определяется предел функции справа:
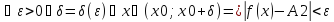
Пределы функции слева и справа называются односторонними пределами.
Если существует
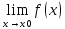 =А,
то существуют и оба односторонних
предела, причем А=А1=А2.
=А,
то существуют и оба односторонних
предела, причем А=А1=А2.
Справедливо
и обратное: если существуют
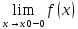 =А1
и
=А1
и
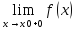 =А2
и они равны, то существует предел
=А2
и они равны, то существует предел
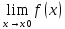 =А.
=А.
Если А1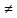 A2
то предел
A2
то предел
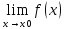 =А
не существует.
=А
не существует.
Бесконечно малые функции (БМФ)
Определение:
Функция y=f(x)
называется БМФ при x->x0,если
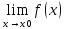 =0
=0
По определению предела:
для любого ε >0 существует такое δ > 0,что для любого x при котором истинно неравенство 0<|x-x0|< δ, следует: |f(x)|< ε
Аналогично определяется бмф при x->x0+0 , x->x0-0, x->+-∞
Во всех этих случаях f(x) ->0
Бесконечно малые функции обычно называют бесконечно малыми величинами, и обозначают греческими буквами α,β и т.д.
Основные теоремы:
1) Алгебраическая сумма конечного числа бесконечно малых функций есть величина БМФ.
2)Произведение ограниченной функции на бесконечно малую функцию есть величина бесконечно малая.
3) Так как всякая бмф ограничена, то из Теоремы 2 следует: произведение двух бесконечно малых есть величина бм.
Следствие Т3: Произведение бмф на число есть бесконечно малая.
4)Частное от деления бесконечно малой функции на функцию, имеющую отличный от нуля предел, есть бмф
5)Если функция α=f(x) – бм. (α не равно 0), то функция 1/a(x) – есть бесконечно большая функция и наоборот: Если f(x) – бесконечно большая, то 1/f(x) – есть бм.
Связь между пределои и бесконечно малой фйнкцией:
Т1) Если
функция f(x)
имеет предел, равный А, то её можно
представить как сумму числа А и бмф
α(x), т.е. если
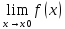 =А,
то f(x)=A+α(x).
=А,
то f(x)=A+α(x).
Основные теоремы о пределах:
1) Предел суммы (разности) двух функций равен сумме (разности) их пределов:
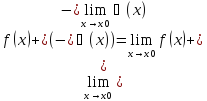
Доказательство:
Пусть
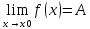 ,
,
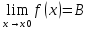 .
Тогда по теореме о связи предела с бм:
.
Тогда по теореме о связи предела с бм:
можно
записать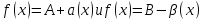 .
.
Следовательно, f(x)+ φ(x)= A+B+(α(x)+β(x))
Здесь в правой
части бмф, как сумма бмф. Тогда по теореме
о связи предела с бмф можно записать
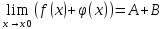 ,
т.е.
,
т.е.
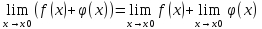
В случае разности доказательство аналогичное.
Следствие 1): Функция может иметь только один предел при x->x0.
Док-во:
Пусть
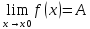 и
и
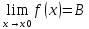 .
По Т1 имеем:
.
По Т1 имеем:
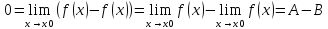
Отсюда А-B=0, т.е. A=B
3) Предел произведения двух функций равен произведению их пределов.
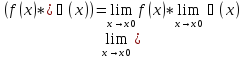
Доказательство аналогичное сумме пределов…
4) Предел дроби равен пределу числителя, деленному на предел знаменателя, если предел знаменателя не равен нулю: