2.4.Нелинейные дискриминантные функции

ЛДФ — это простейшие ДФ, но часто приходится использовать нелинейные ДФ (НЛДФ). Квадратическая функция имеет следующий вид:

Первый набор весов в (2.3.1) в правой части состоит из n весов w_ij= 1,2,…, n, второй набор w_jk j=1,2,…, n-1, k = 2,3,…,n, состоит из n(n-1)/2 весов, и третий - w_jj, j=1,2,…, n – из n весов, и последний набор w_n+1 – только один коэффициент. Отсюда следует, что полное число весов d(x) равно (n+1)(n+2)/2. Выражение 2.31 можно представить в матричной форме.

Отметим, что если все собственные числа λ матрицы А положительны, то квадратичная форма x^TAx никогда не будет отрицательной и x^TAx=0, если = 0. Это значит, что матрица А — положительно определенная и квадратичная форма тоже положительно определенная. Однако, если один или более λ равно 0, в то время как другие положительны, матрица А будет положительно полуопределенной.

Вспомним, что решающая поверхность определяется как

d_j(x) = d_i(x)

или

d_j(x) - d_i(x) = 0

Для квадратического случая квадратическая разделяющая поверхность определяется уравнением

Варианты квадратической поверхности будут определяться матрицей А=(A_i-A_j). Если А положительно определена, то решающая поверхность будет гиперэллипсоидом с осями в направлении собственных чисел. Если А=aI - единичная матрица, то реш. поверхность будет гиперсферой. Если A – положительно полуопределена решающая поверхность есть гиперэллипсоидальный цилиндр , состоящий из пересекающихся областей в виде гиперэллипсоидов меньшей чем n размерности с осями в направлении ненулевых собственных векторов. В другом случае (когда А отрицательно определена) – решающая поверхность – гиперболоид.

2.4. Ф-машины

Ф-машины (φ) вид классификаторов, в которых для классификации используются φ функции. φ функция (обобщенная дискриминантная функция записывается в виде:

где f_i(x); i=1,…,M- линейно независимо вещественные, однозначно определенные функции, независимые отW_i.

Отметим, что φ(х) – линейно относительно W_i, однако, f_i(x)- необязательно предполагается линейным.

В этой системе имеется М+1 степеней свободы. Для примера возьмем ту же нелинейную, которая рассмотрена в 2.4.

Схематически диаграмма φ машины для этой проблемы показана на рис. 2.13.

F блок – это квадратичный процессор и F=(f₁, f₂,…, f_M). Первые n компонент есть , следующие n(n-1)/2 компонент есть все пары и последние n компонент общее число компонент М = n(n+3)/2. Т.о. мы имеем трансформацию n-мерного пространства образов в М-мерное φ-пространство.

2.5.2. Емкость φ-машин для классификации образов.

Вычислим число дихотомий, которые могут быть получены для N образов. Предположим, что М=2 и мы имеем N n-мерных образов. Т.к. каждый образ может попасть либо в w₁, либо в w₂, существует 2^N различных путей, которыми N образов могут быть дихотомизированы. Для N=3 мы будем иметь 8 дихотомий, N=4 – 16 дихотомий. Общее число дихотомий, которое может обеспечить ЛДФ (φ-машина, в φ-пространстве) зависит только от n и N, но не от того, как расположены образы в пространстве образов, образованном φ-функциями.

Пусть D (N, n) будет числом дихотомий, которые могут быть получены линейной машиной (линейные дихотомии) для N образов в n-мерном пространстве. На примере, приведенном на рис. 2.14 для 4 образов показаны все возможные линейные дихотомии.

Каждая линейная поверхность l_i делит образы двумя способами.

Например l_3.

Общее число линейных дихотомий N точек в n-мерном евклидовом пространстве равно удвоенному числу путей, которыми эти точки могут быть разделены (n-1)-мерными гиперплоскостями. Так, D (4,2) = 2*7 = 14. Сравнивая с общим числом возможных дихотомий 2^N = 16, мы находим, что две дихотомии линейно нереализуемы. На рис. видно, что точки (x₁, x₄) и (x₂, x₃) не могут быть линейно разделены. Можно показать, что общее число линейных дихотомий определяется следующим соотношением.

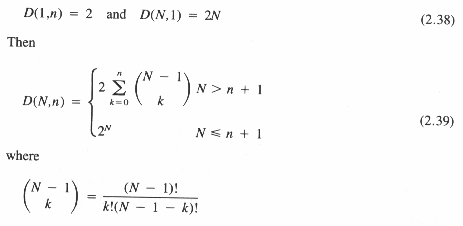
Обобщим эту проблемму нахождения вероятности получить желаемую дихотомию. Для заданной φ-машины и последовательности из N образов в пространстве образов возможно 2^N дихотомий и любая из них может быть выбрана с вероятностью 2^-N. Для обобщенной решающей функции

вероятность P_N,M­ того, что любая дихотомия может быть получена, определяется как:

P_N,M­ = число φ-дихотомий / общее число возможных дихотомий = D(N,M)/ 2^N.

Отметим, что P_N,M=1 для N<=M+1, что означает, что число образов меньше числа возможных весов для обобщенной решающей функции и, соответственно, образы могут быть всегда линейно разделены в М-мерном пространстве образов. Проведенный выше анализ не говорит нам как выбрать d(x) или φ(х), однако он оценивает возможность данной машины осуществлять дихотомию образов. Например, если у нас для двух классов имеется N образов, мы можем быть уверены, что если взять большое М, то всегда найдется подходящий.

Возьмем параметр λ.

N= λ(M+1)

И построим зависимость:

P_{N,M =} P_N,λ

Рис.

Видно, что пороговое значение λ = 0,5. Тогда можно определить дихотомизационную мощность решающего правила как:

С=2(М+1)

Видно, что чем больше размерность, тем больше мощность. Мощность – это пороговое значение длины обучающей выборки при котором еще можно получить заданную дихотомию с достаточно высокой вероятностью.

Линейный классификатор.

Пример: для двух классов в двухмерном пространстве с квадратической ДФ мы имеем

Тогда емкость дихотомизации будет С=2(М+1) = 20

Если N<20 мы имеем возможность надежного выбора.

Этот пример говорит нам сколько нужно иметь элементов в хорошей обучающей выборке.