
- •Эконометрика как наука, определение, основные цели и задачи.
- •Этапы построения моделей, их практическое содержание и особенности.
- •Базовые понятия эконометрики: экономический объект, переменные объекта и их взаимосвязи. Примеры экономических моделей.
- •4. Принципы спецификации эконометрических моделей и их содержание.
- •Классификация переменных эконометрических моделей.
- •Классификация моделей и их формы.
- •7. Формы эконометрических моделей. Переход от структурной к приведенной форме модели.
- •8. Учет случайности характера взаимодействия переменных в экономических объектах. Общий вид эконометрической модели.
- •9. Модели временных рядов, их спецификация.
- •11. Метод наименьших квадратов, основные понятия и определения. Расчет оценок параметров уравнения парной регрессии методом наименьших квадратов.
- •13.Теорема Гаусса-Маркова, основные допущения и предпосылки, их практическое содержание и назначение
- •14.Оценка уравнения парной регрессии с помощью процедур, сформулированных в теореме Гаусса-Маркова.
- •16. Проверка статистических гипотез. Оценка статистической значимости параметров уравнения множественной регрессии.
- •17. Автокорреляция в уравнениях множественной регрессии, признаки ее наличия и последствия.
- •18. Тестирование моделей на присутствие автокорреляции.
- •19.Методы устранения автокорреляции в уравнениях множественной регрессии.
- •20.Гетероскедастичность в уравнениях множественной регрессии, ее признаки, последствия и методы устранения.
- •21.Тестирование моделей на наличие гетероскедастичности, тест Готфельда-Квандта
- •1. Случай уравнения парной регрессии
- •1. Гетероскедастичность приводит к смещенности оценок параметров модели
- •2. Одним из способов обнаружения гетероскедастичности является тест Голдфелда-Квандта
- •3. Взвешенный метод наименьших квадратов позволяет получить несмещенные оценки параметров модели в условиях гетероскедастичности
- •25. Взвешенный метод наименьших квадратов
- •26. Обобщенный метод наименьших квадратов. Теорема Эткейна.
- •27. Построение нелинейных моделей. Методы линеаризации.
- •28. Ошибки спецификации моделей, их последствия и способы устранения.
- •29. Фиктивные переменные и особенности их использования в моделях.
25. Взвешенный метод наименьших квадратов
С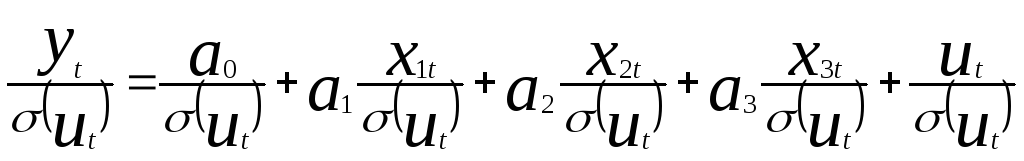 пособ
1. Делится
каждое уравнение наблюдений на свое
σ(ut)
и получается:
пособ
1. Делится
каждое уравнение наблюдений на свое
σ(ut)
и получается:
Т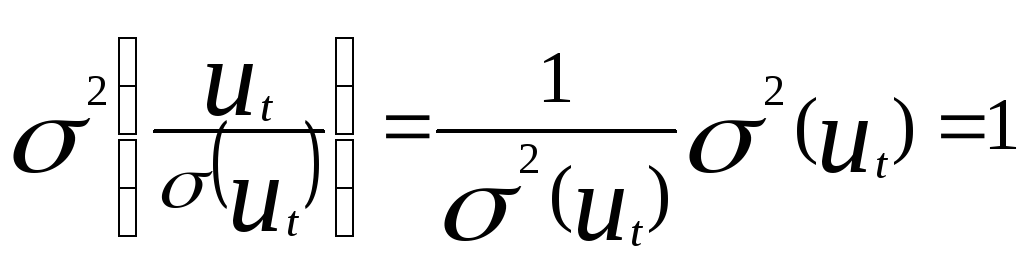 огда
дисперсия случайного возмущения в
каждом уравнении наблюдений есть:
огда
дисперсия случайного возмущения в
каждом уравнении наблюдений есть:
Модель (10.6) в каждом уравнении наблюдения имеет одинаковые дисперсии случайного возмущения равные 1
Недостаток способа – оценить σ(ut) не возможно!
Способ 2.
Предполагаем, что σ(ut)=λxkt, где xkt регрессор «вызывающий» гетероскедастичность Пусть для примера это регрессор x2t
У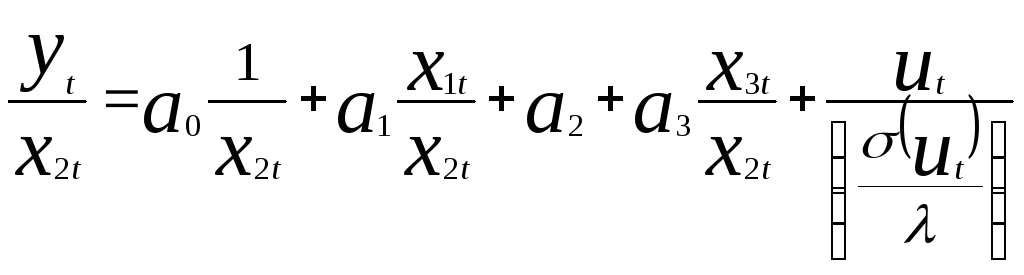 равнение
(10.5) делится на значение этого регрессора.
равнение
(10.5) делится на значение этого регрессора.
Д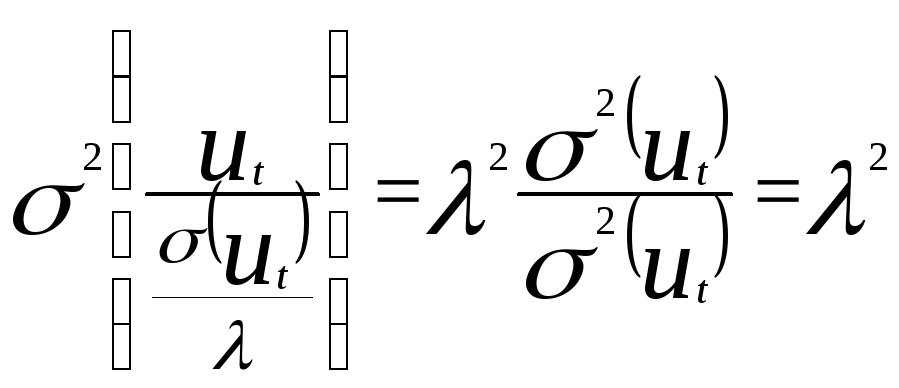 исперсия
случайного возмущения при этом есть:
исперсия
случайного возмущения при этом есть:
Уравнения модели имеют постоянную дисперсию случайного возмущения равную λ2
Е![]() сли
регрессоров, приводящих к
гетероскедастичности,несколько, то
делается предположение:
сли
регрессоров, приводящих к
гетероскедастичности,несколько, то
делается предположение:
О![]() бе
части модели делятся на величину Σ│xj│
бе
части модели делятся на величину Σ│xj│
Т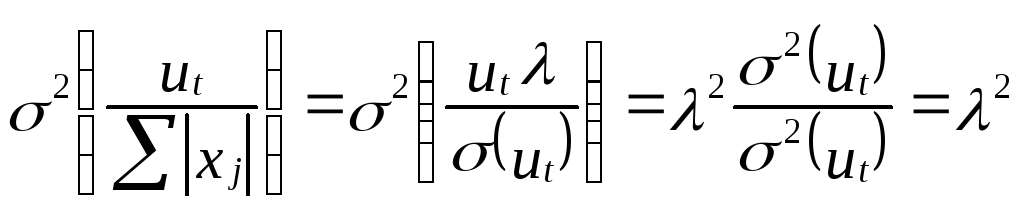 огда
дисперсия случайного возмущения
полученной модели есть:
огда
дисперсия случайного возмущения
полученной модели есть:
П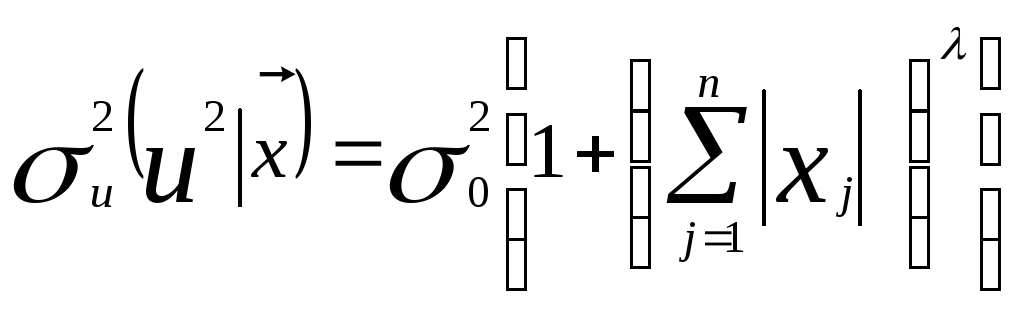 редполагается,
что дисперсию случайного возмущения
можно представить в виде:
редполагается,
что дисперсию случайного возмущения
можно представить в виде:
где: σ02 – дисперсия единицы веса
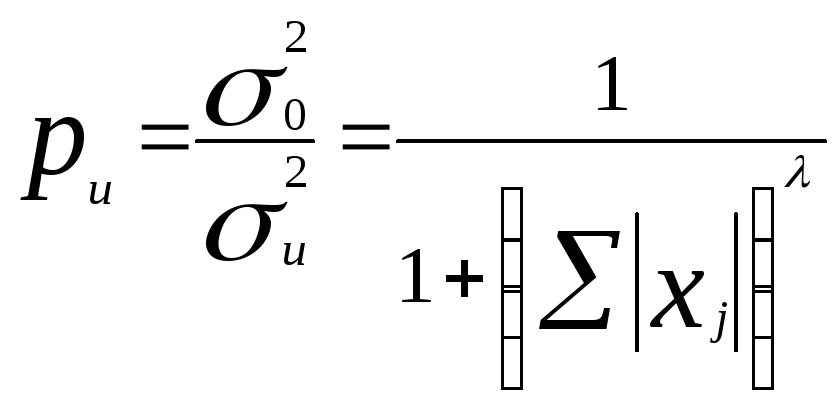 λ
– заданная константа, например ±0.5; ±1;
±2;
λ
– заданная константа, например ±0.5; ±1;
±2;
Вес случайного остатка вычисляется по правилу:
Рассмотренные способы устранения гетероскедастичности носят название «Взвешенный метод наименьших квадратов».
Теорема. Если в схеме Гаусса-Маркова не выполняется предпосылка о гомоскедастичности случайных возмущений, то наилучшей линейной процедурой оценки параметров модели является:
![]()
где: Р матрица ковариаций случайных возмущений в уравнения наблюдений:
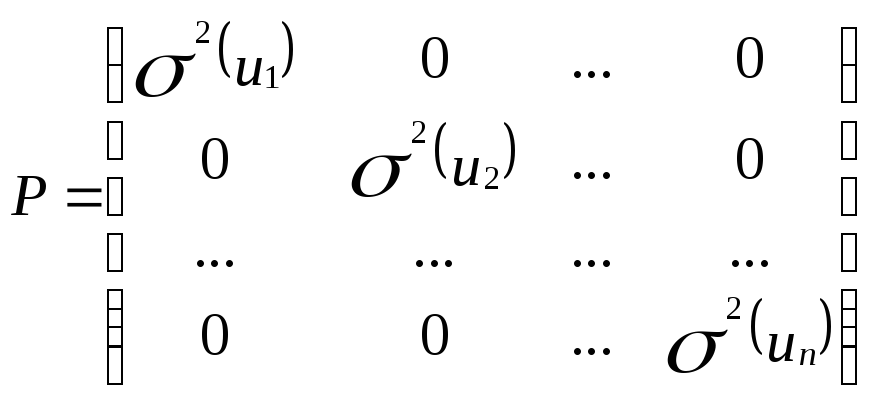
26. Обобщенный метод наименьших квадратов. Теорема Эткейна.
В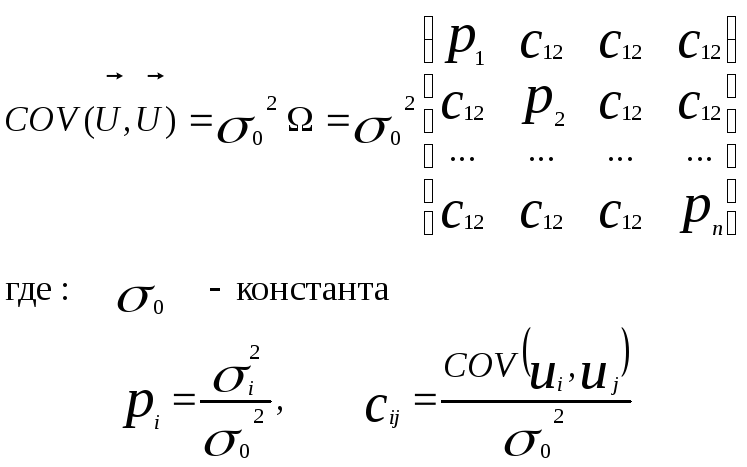 общем случае, когда не выполняются
предпосылки теоремы гаусса-Маркова 2 и
3, тогда:
общем случае, когда не выполняются
предпосылки теоремы гаусса-Маркова 2 и
3, тогда:
Т![]() еорема
Эйткена. Если матрица Х коэффициентов
уравнения наблюдений имеет полный ранг,
М(ui)=0,
а матрица ковариаций случайных возмущений
имеет вид (11.9), то наилучшие оценки
параметров линейной модели множественной
регрессии дает процедура:
еорема
Эйткена. Если матрица Х коэффициентов
уравнения наблюдений имеет полный ранг,
М(ui)=0,
а матрица ковариаций случайных возмущений
имеет вид (11.9), то наилучшие оценки
параметров линейной модели множественной
регрессии дает процедура:
(11.10)
Если: Ω=E, то (11.10) превращается в МНК, а если
pi≠Const, а Cij=0 – (11.10) превращается в ВМНК
27. Построение нелинейных моделей. Методы линеаризации.
О![]() сновные
типы нелинейных моделей:
сновные
типы нелинейных моделей:
1![]() .Обобщенная
модель нелинейная по переменным
.Обобщенная
модель нелинейная по переменным
2![]() .
Степенные функции
.
Степенные функции
3. Показательные функции
О![]() бобщенная
модель нелинейная по переменным (1)
бобщенная
модель нелинейная по переменным (1)
Л![]() инеаризация
обобщенной нелинейной модели
инеаризация
обобщенной нелинейной модели
-
Вводятся новые переменные:
2![]() .
Подставляя новые переменные в модель
(1), получим модель линейную по переменным
z:
.
Подставляя новые переменные в модель
(1), получим модель линейную по переменным
z:
3. После оценки параметров модели делается обратный переход к модели (1.1)
П![]() римеры.
римеры.
-
П
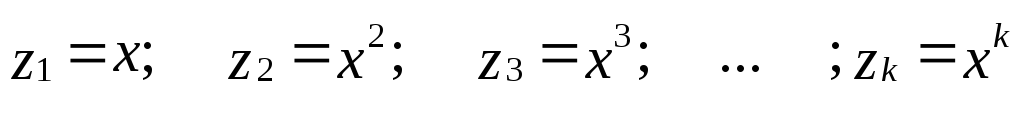 олиномиальные
модели:
олиномиальные
модели:
Н![]() овые
переменные:
овые
переменные:
-
Модели гиперболического типа
Н![]() овая
переменная:
овая
переменная:
Степенная модель, показательная модель, экспоненциальная модель линеаризуются логарифмированием.
