Вопрос 20. Мат. Ожидание, дисперсия и среднее квадратическое отклонение среднего арифметического одинаково распределенных взаимно независимых величин.

теорема1:

Пусть даны независимые величины, причём случайные величины одинаково распрелелены.

Тогда математическое ожидание их среднего арифметического где - математическое ожидание каждой из случайных величин.

теорема 2:

теорема 3:

- число случайных величин

Вопрос 21. Неравенство Чебышева.

Вероятность того что случайные величины отклоняются от своего математического ожидания на величину меньше чем не меньше чем

			…

Если то она отклоняется от своего математического ожидания меньшего

Для выполняется (4)

В отдельности каждая из вероятностей , где , выражает вероятность того что случайная вероятность примет значение равное для которого будет выполняться неравенство (4), т. е. сумма всех этих вероятностей представляет собой вероятность осуществления неравенства (4).

Вопрос 22. Теорема Чебышева.

Вероятность того что случайная величина равная среднему арифметическому независимых случайных величин отклонится от среднего арифметического собственных математических ожиданий на величину не превосходящую любого как угодно малого при условии что число случайной величины велико.

Случайные величины предполагаются с ограниченными дисперсиями.

Рассмотрим

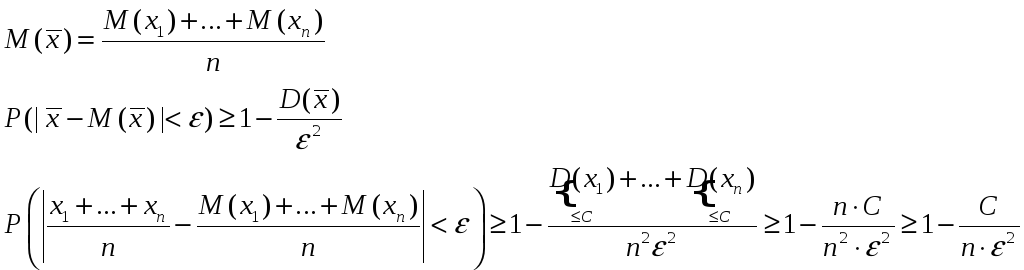
т.к. не может быть больше единицы, то .

Следствие:

Если случайные величины одинаково распределены (имеют одинаковые численные характеристики математического ожидания и дисперсии) тогда

Несмотря на то что каждая в отдельности величина носит случайный характер распределения. Среднее арифметическое большого числа случайных величин утрачивает характер случайной величины. Происходит это за счёт отклонения от своего математического ожидания случайной величины может быть как положительным так и отрицательным. А в совокупности положительные и отрицательные величины взаимнопогашаются.

Вопрос 23. Теорема Бернулли.

Если достаточно велико и в независимых испытаниях вероятность появления некоторого события постоянна и равна , то вероятность того, что относительная частота появления события отклонится от своей вероятности на величину меньше равна единице.

Пусть случайная величина равная числу появления в независимых испытаниях

	0	1

Покажем что к можно применить теорему Чебышева.

применим следствие

т. к. событие произойдёт раз, то

Сходимость к вероятности понимается не в смысле классического математического анализа а в смысле формулы .