18.Теория нечетких множеств – основные определения

Нечеткое множество (fuzzy set) – представляет собой совокупность елементов произвольной природы, относительно которых нельзя с полной уверенностью утверждать: принадлежит ли тот, или иной элемент данному множеству, или нет? Математическое определение нечеткого множества – нечеткое множество à определяется как множество упорядоченных пар или кортежей вида à ={ < x, µ_à (x)>}, где: х- элемент некоторого универсального множества х є Х; µ_A(x) – функция принадлежности, которые ставит в соответствие каждому из элементов пространства Х некоторое действительное число из интервала [0;1]; 0 – не принадлежит точно, 1 – точно принадлежит. Пустое нечеткое множество Ø – множество, которое не содержит ни одного элемента, формально оно определяется как нечеткое множество, функции принадлежности которого, для всех без исключения элементов тождественно равны нулю. µ_Ø≡0. Универсальное множество или универсум Ẽ, формально оно определяется как нечеткое множество, функции принадлежности которого, для всех без исключения элементов тождественно равны 1. µ_Ẽ≡1 Носитель нечеткого множества à – называется обычное множество А_s , которое содержит только те элементы универсума, для которых значение функции пренадлежности отлично от нуля. А_s ={xєX| µ_Ã>0} Нечеткое множество – называется конечным, если его носитель являеться конечным множеством. Бесконечное нечеткое множество – называется множество, носитель которых также является бесконечным множеством. Счетным нечетным множеством – называются нечеткие множество со счетным носителем. Континуальным – нечеткое множество с несчетным носителем.

19. Примеры нечетких множеств и их функций принадлежности. Операции над нечеткими множествами.

Примеры нечетких множеств Пр.1. Множество – дни недели Е={Пн,Вт,Ср,Чт,Пт,Сб,Вс}А={Сб,Вс} – выходные

Пр2.

Множество коффе, насколько он горячий

Е=[0⁰,100⁰]

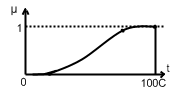
Пр.3

Сканирование изображения

Е={А,Б,В,..,Я}

Ã={<А;0>,…,<Н;0,8>,<К;0,5>}

0, х ≤ а

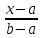, a<x<b

µ(х)=

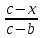, b ≤ x<c

0, x ≥ c

Операции над нечеткими множествами сводяться к операциям над их пренадлежностями:

1)максиминная

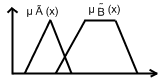
Ã= µ_с(х)=max(µ_A, µ_B)

à ∩ = µ_с(х)=min(µ_A, µ_B)

2) алгебраическая

= Ã => µ_с(х) = µ_A(х)+ µ_B(х)- µ_A(х)∙ µ_B(х)

= Ã∩ => µ_с(х) = µ_A(х)∙µ_B(х)

3) ограниченная

µ _{А В} (х) = min {1; µ_A(х)+ µ_B(х)}

µ _{А∩ В} (х) = max {0, µ_A(х)+ µ_B(х) -1}

Дополнения:

µ _А =1- µ_B

20. Нечеткая логика, ее основное отличие от логики предикатов. Понятие нечеткой и лингвистической переменной.

Понятие нечёткой логики было впервые введено профессором ЛотфиЗаде в 1965 году. В его статье понятие множества было расширено допущением, что функция принадлежности элемента к множеству может принимать любые значения в интервале [0...1], а не только 0 или 1. Такие множества были названы нечёткими. Также автором были предложены различные логические операции над нечёткими множествами и предложено понятие лингвистической переменной, в качестве значений которой выступают нечёткие множества. Логика предикатов – основной раздел современной логики, в котором описываются выводы, учитывающие внутреннюю (субъектно-предикатную) структуру высказываний. Нечёткая логическая переменная может быть описана тройкой параметров <a, X, А>, где: а — имя нечёткой переменной; Х — универсальное множество, на котором заданы значения переменной а; A — нечёткое подмножество универсального множества X, для каждого элемента которого определена функция m(x), задающая степень принадлежности данного элемента к множеству А. Параметр A может быть задан различными способами: табличным, графическим, аналитическим. Пример. а = «Высокий рост»; X — множество натуральных чисел N;

A = {150/0 + 160/0.1 + 170/ 0.2 + 180/0.5 + 190/0.7 + 200/0.9 + 210/1} (табличное представление). Лингвистической переменной называется пятерка {x,T(x),X,G,M}, где x — имя переменной; T(x) — множество имен лингвистических значений переменной x, каждое из которых является нечеткой переменной на множестве X; G есть синтаксическое правило для образования имен значений x; M есть семантическое правило для ассоциирования каждой величины значения с ее понятием. Пример: Рассмотрим лингвистическую переменную, описывающую возраст человека, тогда: x: «возраст»;

X: множество целых чисел из интервала [0, 120]; T(x): значения «молодой», «зрелый», «старый»; G: «очень», «не очень». Такие добавки позволяют образовывать новые значения: «очень молодой», «не очень старый» и пр. M: математическое правило, определяющее вид функции принадлежности для каждого значения из множества T.