24. Основные операции над нечеткими отношениям.

Пусть на множестве заданы X˟X два нечетких отношения A и B с функциями принадлежности μ_A(x,y),μ_B(x,y). Тогда множество C=AB представляет собой объединение нечетких отношений A и B на множестве X ,если его функция принадлежности определяется выражением. 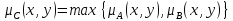.Аналогично множество D=A∩B является пересечением нечетких множеств A и B, если 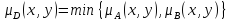.Можно ввести также операции сильного объединения и сильного пересечения, аналогичные операциям над нечеткими множествами. Нечеткое отношение B включает в себя нечеткое отношение A(A) , если для них выполняется соотношение 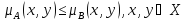. Если R-нечеткое отношение с функцией принадлежности 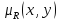, то отношения 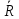, характеризующееся функцией принадлежности называется дополнением R на множестве X.Обратное к R отношение на X определяется следующим образом: , при этом функции принадлежности связаны между собою равенством .

25. Композиция нечетких отношений. Применение композиции к оценке проф. Пригодности сотрудников

Важное значение в теории нечетких множеств имеет композиция (или произведение) нечетких отношений. В отличие от обычных (четких) отношений композицию (произведение) нечетких отношений можно определить разными способами. Максиминная композиция (произведение) нечетких отношений A и B на X характеризуется функцией принадлежности вида 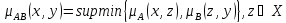. Минимаксная композиция нечетких отношений и на (обозначается ) определяется функцией принадлежности вида . Максимультиплекативная композиция нечетких отношений и на есть нечеткое отношение с функцией принадлежности вида .

26. Основы нечеткой логики. Понятие нечеткого высказывания и нечеткого предиката.

множество истинностных значений высказываний обобщается до интервала действительных значений [О, 1], что позволяет высказыванию принимать любое значение истинности из этого интервала. Это численное значение является количественной оценкой степени истинности высказывания, относительно котopoгo нельзя с полной уверенностью заключить о eгo истинности или ложности. Использование в качестве множества истинностных значений интервала [О, 1] позволяет построить логиче­скую систему, в рамках которой оказалось возможным выполнять рассуждения с неопределенностью и оценивать истинность высказываний типа: "Скорость aв­томо6иля довольно высокая", "Давление в системе весьма значительное", "Высота полета самолета предельно низкая" и др. Исходным понятием нечеткой логики является понятие элементарного нечеткого высказывания. В общем случае элементарным нечетким высказыванием называется повествовательное предложе­ние, выражающее законченную мысль, относительно которой мы можем судить об ее истинности или ложности только с некоторой степенью уверенности.

Сами элементарные нечеткие высказывания иногда называют просто нечеткими высказываниями .

Нечеткий предикат P(<x1, x2,..., xk>) или, более строгого, k-­местный нечеткий предикат, формально определяется как некоторое отображение из декартова произведения универсумов Х1, Х2,..., Хk. В некоторое вполне упорядоченное множество значений истинности, в частности, в интервал [0,1], т. е. Р: XI*X2*...*Xk­[0, 1]. По аналогии с обычными предикатами, пере­менные XI, Х2,..., X k называются предметными переменными нечеткого предиката P«х1, х2,..., х k », а декартово произведение универсумов XI*X2*...*X k ­ eгo предметной областью. В свою очередь взаимосвязь между нечеткими высказываниями и нечеткими предикатами устанавливается с помощью процесса так называемого означивания нечеткого предиката P(<x1, x2,..., x k >), под которым понимается подстановка вместо предикатных переменных xI, x2,..., x k конкретных значений из cоответствующих универсумов: а1 є XI, а2 є Х2,..., а3 є Хk, В этом случае нечеткий предикат P(<x1, x2,..., x k >) превращается в некоторое нечеткое высказывание ρ, которое принимает конкретное значение истинности, равное числу из интервала [0, 1].