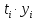Задача 7.16
Имеются следующие данные о товарообороте и издержках обращения предприятий торговой компании.
|
Издержки обращения на 100р. Товарооборота, руб. |
Число предприятий |
Товарооборот в среднем на одно предприятие, млн.р |
Товарооборот в расчете на одного работника, тыс.р |
|
До 3 |
4 |
25 |
1000 |
|
3-4 |
6 |
24 |
923 |
|
4-5 |
10 |
23 |
821 |
|
5-6 |
12 |
20 |
690 |
|
6 и выше |
8 |
18 |
600 |
|
Итого |
40 |
- |
- |
Определите по компании в целом:
А) Средний уровень издержек обращения на 100 руб. товарооборота
Б) Средний размер товарооборота в расчете на одно предприятие
В) Средний размер товарооборота в расчете на одного работника
Решение:
А) Средний уровень издержек обращения на 100 руб. товарооборота = Все издержки/ Весь товарооборот = (2.5*48*25 + 3.5*6*24 + 4.5*10*23+5.5*12*20+6.5*8*18) / (25*4+6*24+….+8*18) = … (руб/100 руб)
Б) Средний размер товарооборота в расчете на одно предприятие = Весь товарооборот / Кол-во предприятий = 110.000.000 / 40 = 2.750.000 млн.р/предпр.
В) Средний размер товарооборота в расчете на одного работника = Весь товарооборот / Все работники = 110.000.000 / (4*25000/1000 + 6*24000/923 + 10*23/821 + 12*20/690 + 8*18/600) = 110.000.000/1124 = 9786.4
Задача 7.18
|
Номер филиала |
Базисный период |
Отчетный период |
|||||
|
Себестоимость единицы продукции, руб. |
Затраты на выпуск продукции, тыс. руб. |
Себестоимость единицы продукции, руб. |
Выработано продукции, тыс.шт. |
||||
|
1 |
22,0 |
10560 |
19,8 |
50 |
|||
|
2 |
21,8 |
19620 |
18,0 |
95 |
|||
|
3 |
22,2 |
12210 |
21,6 |
54 |
|||
Определить среднюю себестоимость единицы продукции по организации в целом:
А) в базисном периоде
Б) в отчетном периоде
Укажите, какие виды средних величин необходимо применить в каждом случаи. Сравните полученные показатели. Объясните, какие факторы оказали влияние на изменение средней с/с единицы продукции в отчетном периоде по сравнению с базисным.
Решение:
А) в базисном периоде:
Ср. себестоимость = Все затраты / Кол-во изделий.
баз
= (10560 + 19620 + 12210) / (10560/22 + 19620/21.8 + 12210/22.2) =
220 руб
Расчет себестоимости по средней гармонической взвешанной.
Б) в отчетном периоде:
отч
= (19.8*50 + 18*95 + 21.6*54) / (50+ 95+54) = 3866.4 / 199 = 19.429
Расчет по средней арифметической.
Рассчитаем средний показатель : (22*50 + 21.8*95 + 22.2*54) / (50+ 95+54) = 219 руб.
Общая себестоимость единицы продукции снизилась с базисного по отчетный период на (19.429-220= -200.571) 200.571 рублей за счет влияния факторов:
1) За счет изменения индивидуальной себестоимости продукции по филиалам:
Z¯ср1 – Zусл = 19,429 – 219 = - 199.571 руб/шт
2) За счет структурных сдвигов в выработке продукции по филиалам
Zусл - Z¯0 = 219 – 220 = - 1 руб/шт
Задача 7.21
|
Номер филиала |
Фактический выпуск продукции в отчетном периоде, тыс. руб |
Изменение выпуска продукции в отчетном периоде по сравнению с базисным, % |
Удельный вес экспортируемой продукции в выпуске отчетного периода, % |
|
1 |
2440 |
-4.5 |
25 |
|
2 |
2520 |
+3.6 |
12 |
|
3 |
2610 |
+5.2 |
15 |
Определите по организации в целом:
А) средний процент изменения выпуска продукции по сравнению с базисным периодом:
Б) средний удельный вес экспортируемой продукции в фактическом выпуске отчетного периода
Решение:
А) средний процент изменения выпуска продукции по сравнению с базисным периодом:
=
Выпуск в отч. периоде / Выпуск в базисном
периоде
-4,5% = 2440 / a0 * 100% - 100%
95.5% = 2440 / a0 * 100%
0.955 = 2440 / a0
a01 = 2440/0.955 = 2554.97
a02 = 2520/1.036 = 2432.43
a03 = 2610/1.052 = 2480.99
=
(2440 + 2520 + 2610) / (2554.97 + 2432.43 + 2480.99) = 1.014
Средний процент прироста равен + 1,04%
Б)
= экспортируемая продукция / Выпуск в
отч. периоде = (2440*0.25 + 2520*0.12 + 2610*0.15) / (2440
+ 2520 + 2610) = 1303.9 / 7570 = 0.1722 - средняя арифметич.
взвеш.
Задача 7.22 (7.23-решается по тем же формулам)
|
Рост, см. |
Численность студентов |
|
До 162 |
30 |
|
162-166 |
40 |
|
166-170 |
45 |
|
170-174 |
55 |
|
174-178 |
40 |
|
178-182 |
30 |
|
182 и более |
20 |
|
Итого |
260 |
Определите моду и медиану роста студентов, децили
|
Xi |
fi |
Sn |
Xi* fi |
|
До 162 |
30 |
30 |
4800 |
|
162-166 |
40 |
70 |
6560 |
|
166-170 |
45 |
115 |
7560 |
|
170-174 |
55 |
170 |
9460 |
|
174-178 |
40 |
210 |
7040 |
|
178-182 |
30 |
240 |
5400 |
|
182 и более |
20 |
260 |
3680 |
|
Итого |
260 |
- |
44500 |
1)
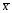= ∑ Xi* fi / ∑ fi = 171.2
2) Мода:
где хМо – нижняя граница модального интервала;
iМо – величина модального интервала;
fМо – частота модального интервала;
fМо-1 – частота, предшествующая модальному интервалу;
fМо+1 – частота интервала, следующего за модальным.
fmax = 55, сл-но, 170-174
Мода = 170 + 4 *[ (55-45) / ( (55-45) + (55-40) ) ] = 171.6
3) Медиана:
где хМе – нижняя граница медианного интервала;
iМе – величина медианного интервала;
fМе – частота медианного интервала;
SМе-1 – сумма накопленных частот, предшествующих медианному интервалу;
Nme = åfi/2 – полусумма частот ряда.
Расчет медианы:
åfi/2 = 260/2 = 130, сл-но, Sme = 120 , сл-но, 170-174
Me = 120 + 4 *[(130-45) / 55] = 176.2
4) Квартель первый :
,
где NQ1
= ∑fi
/ 4 = 260 / 4 = 65, сл-но, Sn=70
, сл-но, 162-166.
Q1 = 162 + 4 * [(65-30)/40] = 164.5
Квартель третий :
,
где NQ3
= [3* ∑fi
]/ 4=(3* 260)/4 = 195, сл-но, Sn=210
, сл-но, 174-178.
Q1 = 174 + 4 * [(195-170)/40] = 176.5
5) Дециль восьмой:
D8 = Xd8 + dd8 * [ (8/10 * ∑fi) - S d8-1] / fd8
Nd8 = (8/10 * ∑fi) = 208, сл-но, Sn=210 , сл-но,174-178.
D8 = 174+ 4*[ (208-170) / 40] = 177.8
Первый, второй, седьмой и девятый децили рассчитываются по тому же принципу, меняя только в формуле число «8/10» на «1/10» , «2/10», «7/10», «9/10».
6) Показатели вариации:
1.
= ∑ Xi*
fi
/ ∑ fi
= 171.2
2. Размах вариации : R = xmax – xmin = 186-158 = 28
3. Среднее линейное отклонение :
-
для несгруппированных данных (первичного
ряда):
-для
вариационного ряда:
=
1596/260 = 6.14
4. Дисперсия
-
для несгруппированных данных:
-
для вариационного ряда:
=
13942.4/260 = 53.6
=
корень из
= 7.32
5. Коэффициент вариации
-
до 17% – совокупность совершенно однородна,
17%-33% - достаточно однородна, >33% -
неоднородна.
V = (7.32 / 171.2) * 100% = 4.27%
6. Коэффициент вариации линейный (относительное линейное отклонение)
V
= (dср
/
)
* 100% = (
6.14 / 171.2) * 100% = 3.59%
7. Коэффициент ассоциации
V
= (R
/
)
* 100% = (28/171.2) *100 = 16.35%
Задача 8.28
|
Группа банков |
Доходность,% |
Число банков |
|
С низким уровнем IT
|
10-15 |
10 |
|
15-20 |
15 |
|
|
20-25 |
20 |
|
|
С высоким уровнем IT
|
25-30 |
40 |
|
30-35 |
10 |
|
|
35-40 |
5 |
Рассчитать дисперсии:
А) внутригрупповые;
Б) среднюю из внутрегрупповых;
В) межгрупповую;
Г) общую, используя правило сложения дисперсий.
Определите эмпирическое корреляционное отношение. Сделайте выводы.
Решение:
А) Банки с низким уровнем IT
|
С низким уровнем IT |
Доходность % |
Число банков, fi |
Xi |
Xi*fi |
(Xi- |
|
|
10-15 |
10 |
12.5 |
125 |
372.1 |
|
|
15-20 |
15 |
17.5 |
262.5 |
18.15 |
|
|
20-25 |
20 |
22.5 |
450 |
304.2 |
|
Итого |
|
45 |
|
837.5 |
694.45 |
)^2*fi
=
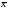∑ Xi*
fi
/ ∑ fi
= 837.5
/ 45 = 18/6%
=
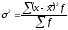694.45/45 = 15.4%
Б) Банки с высоким уровнем IT
|
С высоким уровнем IT |
Доходность % |
Число банков, fi |
Xi |
Xi*fi |
(Xi- |
|
|
25-30 |
40 |
27.5 |
1100 |
132.5 |
|
|
30-35 |
10 |
32.5 |
325 |
101.1 |
|
|
35-40 |
5 |
37.5 |
187.5 |
334.6 |
|
Итого |
|
55 |
|
1612.5 |
568.2 |
)^2*fi
=
∑ Xi*
fi
/ ∑ fi
= 1615.5 /
55 = 29.32
=
568.2 / 55 = 10.3
|
N |
Fj |
|
|
Fj* |
|
(
|
|
1 |
45 |
18.6 |
15.4 |
837 |
693 |
1566.45 |
|
2 |
55 |
29.32 |
10.3 |
1612.6 |
566.3 |
1277.78 |
|
Итого |
100 |
|
|
2449.6 |
1259.5 |
2844.232 |
j
j
j
j*
Fj
j
–
общ
) * Fj
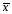общ
= ∑
Xj*
Fj
/ ∑ Fj
= 2449.6 / 100 = 24.5
j
cр
=( ∑
j
*
Fj
) / ∑Fj
= 12.6 – средняя из групповых дисперсий
Межгрупповая
дисперсия (
)
отражает систематическую вариацию, т.
е. различия в величине изучаемого
признака, которые возникают под влиянием
фактора, положенного в основу группировки
,
-
средняя в каждой группе,
-
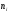число единиц в каждой группе (Fj)
=
28.4
Правило сложения дисперсий:
общ
=
j
cр
+
= 12.6 + 28.44 = 41.04
Эмперическое корреляционное отношение:
,
>0,5
– связь между групповым фактором и
результирующим признаком – тесная,
<0,5
– связь слабая
=
0.83 - связь между уровнем IT
и доходностью высокая.
Задача10.18
При изучении зависимости текучести кадров от уровня оплаты труда получены следующие данные
|
Показатель |
Номер предприятия |
|||||||||
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
|
Оплата труда, тыс. руб. |
20 |
18 |
21 |
21 |
22 |
19 |
10,5 |
10,2 |
11,0 |
9,7 |
|
Коэффициент текучести кадров, % |
1,54 |
1,42 |
1,51 |
1,50 |
1,56 |
1,37 |
1,28 |
1,26 |
1,30 |
1,20 |
Определите:
-
Линейный коэффициент корреляции;
-
коэффициент корреляции рангов Спирмена;
-
коэффициент корреляции знаков Фехнера.
-
Уравнение регрессии
Решение:
- Линейный коэффициент
корреляции
Связь прямая, тесная
-
связь
прямая, тесная -
Связь
прямая, тесная
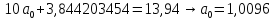
Ответ:
1)
;
2)
;
3)
.
4)
Задача 11.10
Добыа угля в РФ характеризуется следующими данными, млн. т. в год
|
2000 |
2001 |
2002 |
2003 |
2004 |
2005 |
|
258 |
270 |
256 |
277 |
282 |
299 |
Укажите вид ряда динамики. Определите средний уровень добычи угля за 2000-2005 гг.
Решение:
Моментный ряд динамики – значения статистического показателя, относящиеся по состоянию на определенные последовательные моменты времени.
,
где
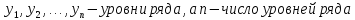
Ответ:
Моментный ряд динамики,
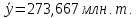
Задача 11.13
За первое полугодие имеем следующие данные о численности безработных, зарегистрированных в органах государственной службы занятости города, тыс. человек.
|
На начало года |
||||||
|
|
|
|
|
|
|
|
|
15,0 |
15,4 |
15,5 |
15,6 |
15,8 |
15,1 |
15,6 |
Укажите ряда динамики. Определите среднюю численность безработных:
а) в январе;
б) в I квартале;
в) во II квартале;
г) в первом полугодии.
Решение:
Моментный ряд динамики – значения статистического показателя, относящиеся по состоянию на определенные последовательные моменты времени.
Ответ: Моментный ряд динамики
а)
б)
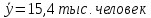
в)
г)
Задача 11.15
Имеем следующие данные о наличии оборотных средств в организации, тыс. руб.
|
Дата |
Сумма |
|
01.01.2007 |
580 |
|
01.04.2007 |
589 |
|
01.07.2007 |
620 |
|
01.10.2007 |
670 |
|
01.01.2008 |
690 |
Укажите ряда динамики. Определите средний остаток оборотных средств в 2007 г.
Решение:
Моментный ряд динамики – значения статистического показателя, относящиеся по состоянию на определенные последовательные моменты времени.
Ответ:
Моментный ряд динамики;
Задача 11.18
Данные о добычи нефти в РФ следующие.
|
Год |
2001 |
2002 |
2003 |
2004 |
2005 |
|
Добыча нефти, млн. т |
348 |
380 |
421 |
459 |
470 |
Для анализа динамики добычи нефти определите:
а) средний уровень ряда;
б) абсолютные приросты (ценные, базисные, средние);
в) среднегодовой абсолютный прирост за 2001-2005 гг.;
г) темпы роста и прироста (ценные, базисные, средние);
д) среднегодовые темпы роста и прироста за 2001-2005 гг.;
е) абсолютное значение одного процента прироста (по годам);
ж) аналитическое выравнивание ряда по прямой;
з) составить прогноз на 3 года вперед ( 3 способами).
Решение:
а)
б)
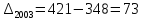
в)
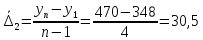
Составим прогноз на 2008 г. На основе среднегодового абсолютного прироста
г) Темпы роста
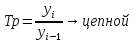
Прироста
Цепной Базисный
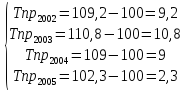
д)
Составим прогноз на 2008 г. На основе среднегодового темпа роста:
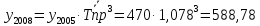
е)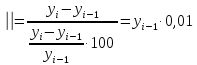
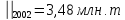
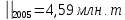
ж) Составим прогноз методом аналитического выравнивания ряда по прямой
|
Год |
Добыча нефти, млн. т |
|
|
|
|
|
2001 |
348 |
1 |
1 |
348 |
351 |
|
2002 |
380 |
2 |
4 |
760 |
383,3 |
|
2003 |
421 |
3 |
9 |
1263 |
415,6 |
|
2004 |
459 |
4 |
16 |
1836 |
447,9 |
|
2005 |
470 |
5 |
25 |
2350 |
480,1 |
|
S |
2078 |
15 |
55 |
6557 |
2077,9 |
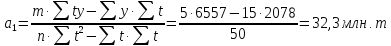
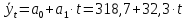смотреть таблицу
Правильность
расчетов проверим равенством :
з) На основании данной модели составим прогноз на 3 года :
Составим прогноз с помощью среднего абсолютного прироста:
Составим прогноз с помощью среднего абсолютного прироста:
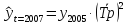
Задача 11.21
Данные о темпах роста объема отгруженной продукции организации следующие
|
Год |
Темп роста, % к 2001 г. |
Темп роста, % к предыдущему году |
|
2002 |
102 |
… |
|
2003 |
… |
102,3 |
|
2004 |
106,6 |
… |
|
2005 |
108,2 |
… |
|
2006 |
… |
102,4 |
|
2007 |
… |
102,8 |
Определите недостающие показатели в таблице. Рассчитайте среднегодовые темпы роста и прироста объема продукции за период с 2002 по 2007 гг.
Решение:
|
Год |
Темп роста, % к 2001 г. |
Темп роста, % к предыдущему году |
|
2002 |
102 |
102 |
|
2003 |
104,3 |
102,3 |
|
2004 |
106,6 |
102,2 |
|
2005 |
108,2 |
101,5 |
|
2006 |
110,8 |
102,4 |
|
2007 |
113,9 |
102,8 |
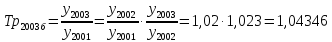
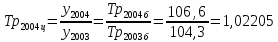
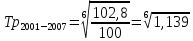
Задача 11.26
Абсолютные приросты объема отгруженной продукции орг-ции характер-ся следующ данными (по сравнению с предыдущ годом)
|
Показатель |
2005 |
2006 |
2007 |
|
Абсолют прирост, млн т |
+1,2 |
+1,4 |
+1,5 |
Известно, что в 2006 г. по сравнению с 2005 г бъем отгруженной прод-ции орган-ции увеличился в 1,04 раза. Определите за рассматриваемый период:
А) среднегодовой абсолютный объем отгруженной прод-ции
Б) среднегодовые темпы роста и прироста объема отгруженной прод-ции
Решение:
∆ пр
=
=
= 1,37
У07 = 37,9
|
год |
2005 |
2006 |
2007 |
|
Объем отгруж прод |
35 |
36,4 |
37,9 |
∆ пр = (3,2 + 36,4 + 37,9) / 3 = 1,3667
Тр
=
= 1,04 или 104%
Тпр = Тр – 100% = 4%
Задача 11.48
Заполните таблицу недостающими показателями.
|
Год |
Страховые взносы, тыс.руб |
По сравнению с предыдущим годом |
|||
|
Абсолютный прирост, тыс.руб |
Темпы роста, % |
Темпы прироста, % |
Абсолютное значение 1% прироста, ты сруб. |
||
|
2002 |
105 |
|
|
|
|
|
2003 |
106,58 |
1,58 |
101,5 |
1,5 |
1,05 |
|
2004 |
108,08 |
+1,5 |
101,4 |
1,4 |
1,066 |
|
2005 |
109,38 |
1,3 |
101,2 |
1,2 |
1,081 |
|
2006 |
111,35 |
1,97 |
101,8 |
+1,8 |
1,094 |