13. Приложения определенного интеграл.

13.1. Некоторые кривые, которые будут встречаться в дальнейшем.

В этом разделе мы рассмотрим некоторые приложения определённого интеграла, в основном, геометрические - к вычислению площадей и объёмов. Здесь мы приведём уравнения и изображения ряда кривых, которые с которыми будем работать дальше.

1. Окружности, проходящие через начало системы координат. Уравнение окружности с центром

радиуса : . Если окружность проходит через начало координат, то , и уравнение принимает вид . В полярных координатах это уравнение выглядит так: . На рисунке справа приведены три такие окружности (), (), ().

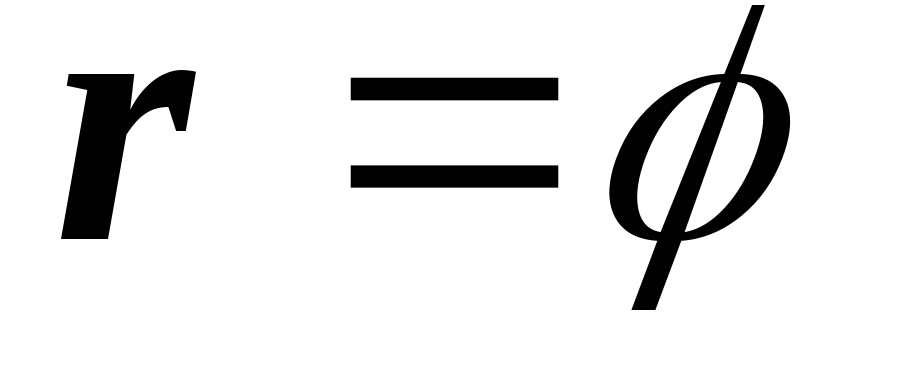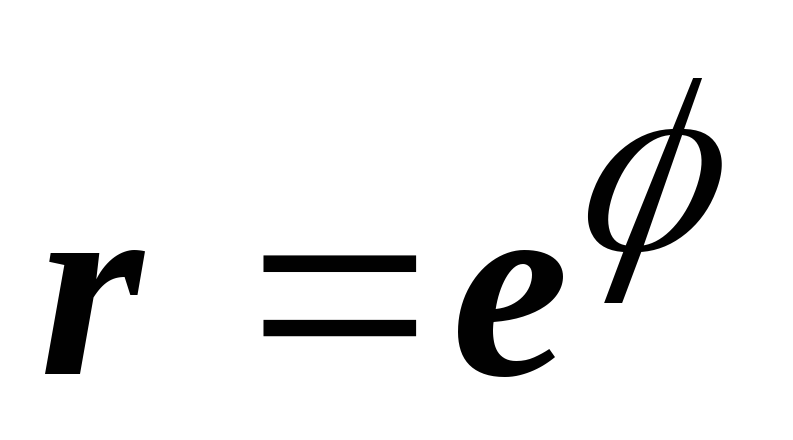2. Спирали: спираль Архимеда . На рисунке изображены спирали и . Логарифмическая спираль . На рисунке изображены спирали и .

Г иперболическая спираль . На рисунке изображены спирали и . Стрелками на всех спиралях указано направление возрастания параметра .

3. К ардиоида . Три таких кривых изображены на рисунке справа.

Декартово уравнение кардиоиды: ;

Параметрические уравнения кардиоиды:

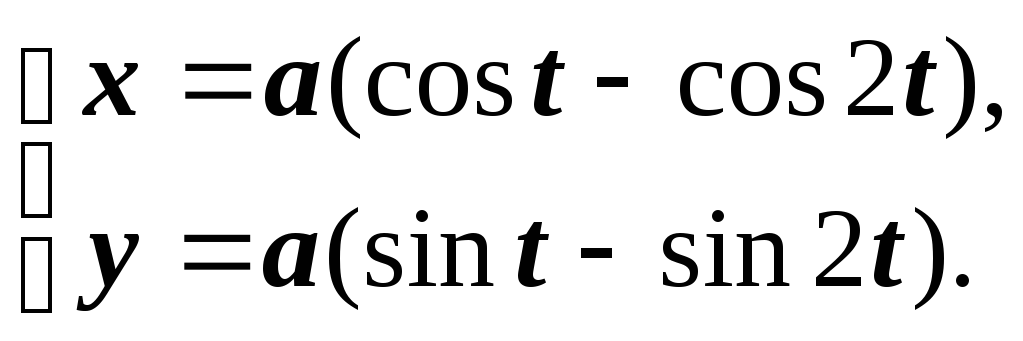
Кардиоида - частный случай улитки Паскаля .

4. Лемниската Бернулли .

П одкоренное выражение неотрицательно при и . Декартово уравнение лемнискаты .

Лемниската - геометрическое место точек таких, что , где и - фокусы лемнискаты.

На рисунке изображена лемниската с .

5. Ч етырёхлепестковая роза . Декартово уравнение .

Каждая точка этой кривой - основание перпендикуляра , опущенного из начала координат на отрезок постоянной длины , движущийся так, что его концы находятся на осях координат.

6. Развёртка (эвольвента) окружности

К аждая точка этой кривой - конец нити, которая разматывается с окружности , оставаясь в натянутом состоянии. В начальный момент конец нити находится в точка .

7. Циклоида

Эта кривая - траектория точки окружности радиуса , которая без скольжения катится по оси . В начальный момент точка находится в точка .

8. Астроида

Д екартово уравнение . Каждая точка этой кривой - основание перпендикуляра , опущенного из начала координат на отрезок постоянной длины , движущийся так, что его концы находятся на осях координат. Точка - вершина прямоугольника, построенного на отрезке как диагонали. На рисунке приведена астроида с .

.

.

.

.

.

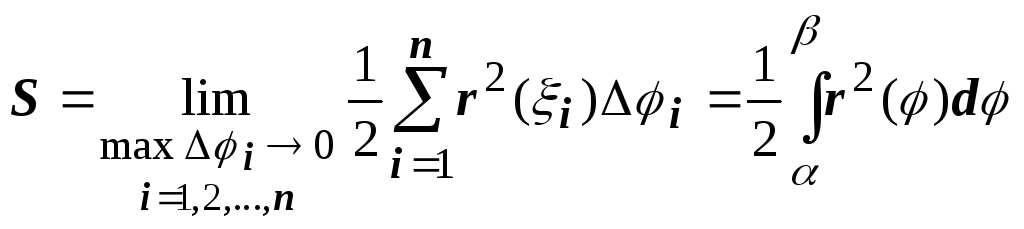13.4. Объёмы тел вращения.

.

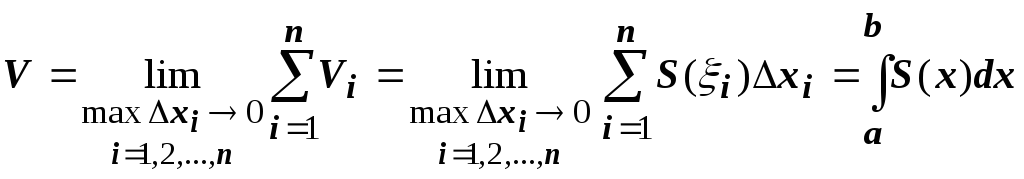Объём тела, получающегося при вращении кривой вокруг координатной оси. .

.

13.4.3. Объём тела, получающийся при вращении сектора, ограниченного кривой и двумя полярными радиусами и , вокруг полярной оси .

13.5. Площадь поверхности вращения.

Площадь поверхности вращения, образующейся при вращении вокруг оси дифференцируемой кривой, определяется по формулам (в зависимости от способа задания кривой)

(- длина окружности кольца, - его ширина).

141