
- •1.Целые и рациональные числа. Действия с целыми и рациональными числами.
- •2.Действительные числа.
- •3.Комплексные числа. Работа с комплексными числами.
- •4. Функции и графики.
- •5. Четные и нечетные функции. Определение четных и нечетных функций.
- •6.Возрастание и убывание функций. Экстремумы функций.
- •7. Преобразование графиков.
- •8. Обратные функции. Область определения и область значения обратной функции.
- •10. Определение тригонометрических функций.
- •11. Свойства тригонометрических функций.
- •12. Основные тождества тригонометрии .
- •13.Формулы сложения.
- •14. Формулы сложения тригонометрических функций.
- •15. Формулы приведения. Формулы двойных и половинных углов.
- •Графики и свойства тригонометрических функций
- •Функция котангенс
- •Функция тангенс
- •Функция косинус
- •22. Квадратные тригонометрические уравнения.
- •23. Однородные тригонометрические уравнения.
- •24.Тригонометрические неравенства.
- •25. Корень n – степени и его свойства.
- •26. Иррациональные уравнения.
- •Пример 1.
- •Пример 2.
- •27. Степень с рациональным показателем.
- •28. Показательная функция: основные понятия, ее свойства и график.
- •29. Показательные уравнения. Решение показательных уравнений .
- •31. Логарифмы и их свойства.
- •32. Десятичные и натуральные логарифмы.
- •33. Логарифмическая функция: основные понятия, ее свойства и график.
- •34. Логарифмические уравнения.
- •35. Основные способы решения логарифмических уравнений.
- •36. Логарифмические неравенства.
- •37. Равносильность уравнений и неравенств.
31. Логарифмы и их свойства.
Логари́фм
числа b по основанию a
-определяется как показатель
степени, в которую надо возвести
основание
a, чтобы получить число b.
Обозначение:
![]() .
Из определения следует, что записи
.
Из определения следует, что записи
![]() и
и
![]() равносильны.
равносильны.
Основное
логарифмическое тождество:
![]()
При любом а>0 (а≠ 1) и любых положительных х и у выполнены равенства:
1. loga1=0.
2. logaa=1.
3. logaxy =logax + logay. Логарифм произведения равен сумме логарифмов.
4.
loga
![]() =logax—logay.
Логарифм частного равен разности
логарифмов.
=logax—logay.
Логарифм частного равен разности
логарифмов.
5. loga xp=p loga x для любого действительного р. Логарифм степени равен произведению показателя степени на логарифм основания этой степени.
32. Десятичные и натуральные логарифмы.
![]() - десятичный логарифм (логарифм по
основанию 10):
- десятичный логарифм (логарифм по
основанию 10):
![]()
![]() - натуральный логарифм (логарифм по
основанию e):
- натуральный логарифм (логарифм по
основанию e):
![]()
Переход от одного основания к другому:
![]()
33. Логарифмическая функция: основные понятия, ее свойства и график.
Функцию, заданную формулой
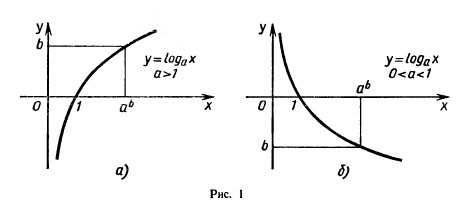
y =logax, называют логарифмической функцией с основанием а.
Основные свойства логарифмической функции. 1. Область определения логарифмической функции — множество всех положительных чисел R+, т. е. D(loga)=R+.Действительно, как отмечалось в предыдущем пункте, каждое положительное число х имеет логарифм по основанию а.
2. Область значений логарифмической функции — множество всех действительных чисел.
3. Логарифмическая функция на всей области определения возрастает (при а>1) или убывает (при 0<а<1).
Графики показательной и логарифмической функций, имеющих одинаковое основание, симметричны относительно прямой у = х.
34. Логарифмические уравнения.
Уравнение, содержащее неизвестное под знаком логарифма или (и) в его основании, называется логарифмическим уравнением.
Простейшим логарифмическим уравнением является уравнение вида
|
loga x = b. |
(1) |
Утверждение 1. Если a > 0, a ≠ 1, уравнение (1) при любом действительном b имеет единственное решение x = ab.
35. Основные способы решения логарифмических уравнений.
I. Решить уравнение
logx(x2 — 3x + 6) =2.
По определению логарифма из этого уравнения следует, что x2 = x2 — 3x + 6, откуда х = 2.
Проверка. При х = 2
logx(x2 — 3x + 6) = log2 (4 — 6 + 6) = log2 4 = 2.
Значит, х = 2 — корень данного уравнения. Ответ, х = 2.
II. Решить уравнение
lg (x2 —17) = lg (x + 3).
Решение подобных уравнений основано на следующем свойстве логарифмов: если логарифмы двух чисел по одному и тому же основанию равны, то равны и сами эти числа. Из этого свойства логарифмов вытекает, что если только данное уравнение имеет корни, то они должны удовлетворять уравнению
x2 —17 = x + 3,
откуда
x1 = 5, x2 = — 4.
Проверка. При х = 5
lg (x2 —17) = lg 8; lg (x + 3) = lg 8.
Значит, х = 5 — корень данного уравнения. При х = —4 левая и правая части данного уравнения не определены, поскольку x2— 17= — 1 < 0 и x + 3 = — 1 < 0. Следовательно, х = — 4 не есть корень этого уравнения.
Ответ, х = 5.
Рассмотрим еще одно уравнение
21g (x— 1) = 1/21g x5 — lg √x (2)
Выполним следующие преобразования:
21g (x— 1) = 1g (x— 1)2,
1/21g x5 — lg √x = lg x5/2 — lg x1/2 = lg x5/2/ x1/2= lg x2.
Таким образом, исходя из уравнения (2), мы пришли к уравнению
1g (x— 1)2 = lg x2. (3)
Из него вытекает, что (x— 1)2 = x2, или х = 1/2. Но при х = 1/2 левая часть уравнения (2) не определена (х — 1 = — 1/2 <0); следовательно, данное уравнение не имеет корней.
Заметим, однако, что для уравнения (3) число 1/2 является корнем. Таким образом, уравнения (2) и (3) не эквивалентны друг другу. Это лишний раз говорит о том, что при решении логарифмических уравнений необходимо делать проверку полученных значений. Среди них часто оказываются «посторонние» корни.
III. Некоторые логарифмические уравнения сводятся к алгебраическим уравнениям посредством введения новой неизвестной величины. Если, например, в уравнении
log3 2 x — 3log3 x — 10 = 0
log3 x обозначить через у, то оно сведется к квадратному уравнению у2 — 3у — 10 = 0, откуда y1 = — 2, y2 = 5. Вспоминая, что у = log3 x, получаем: если log3 x = — 2, то x = 1/9; если же log3 x = 5, то х = 243.
Проверкой легко установить, что оба эти значения х удовлетворяют данному уравнению.
Ответ. x1 = 1/9 ; x2 = 243.
IV. Некоторые уравнения решаются путем почленного логарифмирования. Пусть, например, дано уравнение
![]() =
100.
=
100.
Прологарифмируем это уравнение почленно:
]g
![]() =
lg 100,
=
lg 100,
(lg x— 1) lg x = 2.
Обозначая lg x буквой у, мы приходим к квадратному уравнению
у2 — у — 2 = 0,
имеющему корни y1 = — 1, y2 = 2. Вспоминая, что у = lg x, получаем: либо lg x = — 1, и тогда х = 0,1; либо lg x = 2, и тогда x =100. Проверка. При х = 0,1
![]() =
0,1—1—1 = 0,1—2 = 1/0,01 = 100;
=
0,1—1—1 = 0,1—2 = 1/0,01 = 100;
следовательно, х = 0,1 — корень данного уравнения.
При х = 100
![]() = 1002—1 = 100
= 1002—1 = 100
так что х = 100 — также корень уравнения.
Ответ. x1= 0,1; x2 = 100.
