
- •1.Целые и рациональные числа. Действия с целыми и рациональными числами.
- •2.Действительные числа.
- •3.Комплексные числа. Работа с комплексными числами.
- •4. Функции и графики.
- •5. Четные и нечетные функции. Определение четных и нечетных функций.
- •6.Возрастание и убывание функций. Экстремумы функций.
- •7. Преобразование графиков.
- •8. Обратные функции. Область определения и область значения обратной функции.
- •10. Определение тригонометрических функций.
- •11. Свойства тригонометрических функций.
- •12. Основные тождества тригонометрии .
- •13.Формулы сложения.
- •14. Формулы сложения тригонометрических функций.
- •15. Формулы приведения. Формулы двойных и половинных углов.
- •Графики и свойства тригонометрических функций
- •Функция котангенс
- •Функция тангенс
- •Функция косинус
- •22. Квадратные тригонометрические уравнения.
- •23. Однородные тригонометрические уравнения.
- •24.Тригонометрические неравенства.
- •25. Корень n – степени и его свойства.
- •26. Иррациональные уравнения.
- •Пример 1.
- •Пример 2.
- •27. Степень с рациональным показателем.
- •28. Показательная функция: основные понятия, ее свойства и график.
- •29. Показательные уравнения. Решение показательных уравнений .
- •31. Логарифмы и их свойства.
- •32. Десятичные и натуральные логарифмы.
- •33. Логарифмическая функция: основные понятия, ее свойства и график.
- •34. Логарифмические уравнения.
- •35. Основные способы решения логарифмических уравнений.
- •36. Логарифмические неравенства.
- •37. Равносильность уравнений и неравенств.
22. Квадратные тригонометрические уравнения.
Решим уравнение:
![]()
Надо привести уравнение к одной функции. Для этого заменим cos2 x на 1-sin2x. Получим относительно xinx квадратное уравнение:
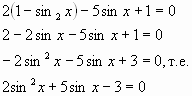
Пусть xinx=у, тогда 2у2+5у-3=0
Получили квадратное уравнение
Д=25+24=49
![]() ;
;
![]()
Следовательно:
а)
![]() б)
xinx=-3 – решение не имеет
б)
xinx=-3 – решение не имеет
![]() ,
к
,
к
![]() z
z
![]() ,
к
,
к
![]() z
z
Ответ:
![]() ,
к
,
к
![]() z
z
4 xin2x- cosx-1=0 Заменим xin2x на 1- cos2x. Получим 4(1- cos2x)- cosx-1=0 4-4 cos2x- cosx-1=0 -4 cos2x- cosx+3=0 4 cos2x+ cosx-3=0
пусть cosx=у, то
4у2+у-3=0
Д=1-48=49
![]() ;
;
![]()
Следовательно,
а) cosx=-1 б)
![]()
х=![]() +2
+2![]() n, n
n, n
![]() z
z
![]() ,
n
,
n
![]() z
z
Ответ:
![]() +2
+2![]() n;
n;
![]() ,
n
,
n
![]() z
z
23. Однородные тригонометрические уравнения.
Определение. Уравнения вида asinx + bcosx=0 называют однородными тригонометрическими уравнениями первой степени; уравнения вида asin2+ bcosxsinx+ ccos2x =0 называют однородными тригонометрическими уравнениями второй степени.
Алгоритм решения уравнения asin2+ bcosxsinx+ ccos2x =0
-
Посмотреть, есть ли в уравнении член asin2х.
-
Если этот член содержится, то уравнение решается делением обеих его частей на cos2x и последующем введением новой переменной z=tgx.
-
Если asin2х не содержится, то уравнение решается методом вынесения общего множителя за скобки.
Существует два метода решения тригонометрических уранений: разложение на множители и введение новой переменной.
Примерами однородных тригонометрических уравнений могут служить уравнения:
sin х — cos х = 0, sin2 х — 5 sin х cos х + 6 cos2 х = 0, cos2 х — sin х cos х = 0.
Решим уравнение sin х — cos х = 0. Для этого заметим, что в данном случае cos x не может быть равен нулю. Если бы было cos х = 0, то должно было бы быть и sin х = 0. Но тогда не выполнялось бы тождество sin2 х +cos2 х = 1. Итак, в данном случае cos х =/= 0. Поэтому обе части данного уравнения можно разделить на cos2 х. В результате получим tg x — 1 = 0, откуда
tg x = 1, х = π/4 + 2nπ
Аналогично решается и уравнение sin2 х — 5 sin х cos х + 6 cos2 х = 0. Разделив обе части этого уравнения на cos2 х, получим:
tg2 х — 5 tg х + 6 = 0; (tg x)1 = 2; (tg x)2 = 3.
Поэтому
x = arctg 2 + nπ х = arctg 3 + kπ.
Теперь решим уравнение cos2 х — sin х cos х = 0.
Здесь уже равенство cos х = 0 возможно, поэтому делить обе части уравнения на cos2 х нельзя. Зато можно утверждать, что sin х =/= 0. В противном случае из уравнения вытекало бы, что cos х = 0. Но тогда не выполнялось бы тождество sin2 х +cos2 х = 1. Итак, sin х =/= 0. Поэтому обе части данного уравнения можно разделить на sin2 х. В результате получим:
ctg2 х — ctg х = 0,
откуда (ctg х)1 = 0; (ctg х)2 = 1. Соответственно этому получаются две группы корней:
х = π/2 + nπ и х = π/4 + kπ
24.Тригонометрические неравенства.
1.
![]()

2.
![]()

3.
![]()

4.
![]()

5.
![]()
6.
![]()
7.
![]()
8.
![]()
25. Корень n – степени и его свойства.
Корень n- степени из числа а это такое число, n-я степень которого равна а.
Арифметическим корнем n- й степени из числа а называют неотрицательное число, n – я степень которого равна а.
Основные свойства

