- •1.Целые и рациональные числа. Действия с целыми и рациональными числами.
- •2.Действительные числа.
- •3.Комплексные числа. Работа с комплексными числами.
- •4. Функции и графики.
- •5. Четные и нечетные функции. Определение четных и нечетных функций.
- •6.Возрастание и убывание функций. Экстремумы функций.
- •7. Преобразование графиков.
- •8. Обратные функции. Область определения и область значения обратной функции.
- •10. Определение тригонометрических функций.
- •11. Свойства тригонометрических функций.
- •12. Основные тождества тригонометрии .
- •13.Формулы сложения.
- •14. Формулы сложения тригонометрических функций.
- •15. Формулы приведения. Формулы двойных и половинных углов.
- •Графики и свойства тригонометрических функций
- •Функция котангенс
- •Функция тангенс
- •Функция косинус
- •22. Квадратные тригонометрические уравнения.
- •23. Однородные тригонометрические уравнения.
- •24.Тригонометрические неравенства.
- •25. Корень n – степени и его свойства.
- •26. Иррациональные уравнения.
- •Пример 1.
- •Пример 2.
- •27. Степень с рациональным показателем.
- •28. Показательная функция: основные понятия, ее свойства и график.
- •29. Показательные уравнения. Решение показательных уравнений .
- •31. Логарифмы и их свойства.
- •32. Десятичные и натуральные логарифмы.
- •33. Логарифмическая функция: основные понятия, ее свойства и график.
- •34. Логарифмические уравнения.
- •35. Основные способы решения логарифмических уравнений.
- •36. Логарифмические неравенства.
- •37. Равносильность уравнений и неравенств.
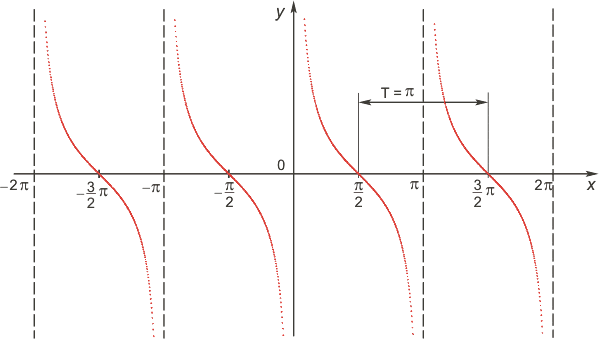
Функция котангенс
![]()
|
|
||||||||||
|
Множество значений функции — вся числовая прямая, т.е. котангенс — функция неограниченная. Функция нечетная: ctg(−x)=−ctg x для всех х из области определения. График функции симметричен относительно оси OY. Функция периодическая с наименьшим положительным периодом π, т.е. ctg(x+π·k)=ctg x, k ∈ Z для всех х из области определения.
|
18. Свойства и график тригонометрической функции y=tg x.
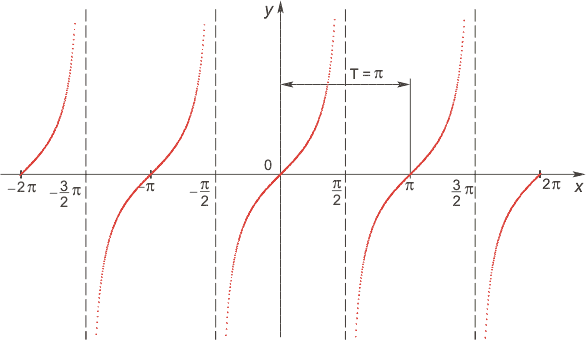
Функция тангенс
![]()
|
|
||||||||||
|
Множество значений функции — вся числовая прямая, т.е. тангенс — функция неограниченная. Функция нечетная: tg(−x)=−tg x для всех х из области определения. График функции симметричен относительно оси OY. Функция периодическая с наименьшим положительным периодом π, т.е. tg(x+π·k) = tg x, k ∈ Z для всех х из области определения.
|
19. Свойства и график тригонометрической функции y=cos x.
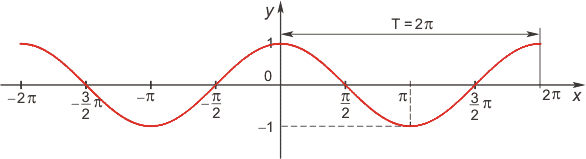
Функция косинус
![]()
|
|
||||||||||||||
|
|
||||||||||||||
|
Область определения функции — множество R всех действительных чисел. Множество значений функции — отрезок [-1; 1], т.е. косинус функция — ограниченная. Функция четная: cos(−x)=cos x для всех х ∈ R. График функции симметричен относительно оси OY. Функция периодическая с наименьшим положительным периодом 2π: cos(x+2π·k) = cos x, где k ∈ Z для всех х ∈ R.
|
20. Простейшие тригонометрические уравнения cos x=a, ctg x=a.
![]()
Частные случаи
![]()
![]()
![]()
![]()
Частные случаи
![]()
![]()
![]()
21. Простейшие тригонометрические уравнения sin x=a, tg x=a.
![]()
Частные случаи
![]()
![]()
![]()
![]()
Частные случаи
![]()
![]()
![]()