10. Определение тригонометрических функций.

Синус, - отношение катета, лежащего против этого угла, к гипотенузе.

КО́СИНУС - катета, прилегающего к острому углу в прямоугольном треугольнике, к гипотенузе.

ТА́НГЕНС - отношение катета, лежащего против острого угла в прямоугольном треугольнике, к другому катету

КОТА́НГЕНС отношение катета, прилегающего к острому углу в прямоугольном треугольнике, к другому катет. Синус отвечает за ось у, а косинус за ось х

11. Свойства тригонометрических функций.

Числовые функции,заданные формулами y=sinx и у=cosx называются соответственно синусом и косинусом.

1. D(sin)=D(cos)=R

2. E(sin)=E(cos)=[-1;1]

3. Cosx – четная

4. Sinx –нечетная

5. T(sin)=T(cos)=2

Числовые функции, заданные формулами y=tgx и y=ctgx называют соответственно тангенсом и катангенсом.

1. D(tg)=( \2 -n; \2+n)

2. E(tg)=R

3. T(tg)=

4. Tgx – нечетн

5. D(ctg)= R, кроме х=n

D(ctg)=(0+n; +n)

6. E(ctg)=R

7. Ctgx –нечетн

8. T(ctgx)=

Функция называется периодической с периодом Т не равным 0, если для любого х из области определения значения этой функции в точках х, х-Т, х+Т равны, т.е f(x+T)=f(x)=f(x-T)

12. Основные тождества тригонометрии .

Основные тригонометрические тождества

• sin² α + cos² α = 1

• tg α · ctg α = 1

• tg α = sin α \ cos α

• ctg α = cos α \ sin α

• 1 + tg² α = 1 \cos² α

• 1 + ctg² α = 1 \ sin² α

13.Формулы сложения.

Формулы сложения

• sin (α + β) = sin α · cos β + sin β · cos α

• sin (α - β) = sin α · cos β - sin β · cos α

• cos (α + β) = cos α · cos β - sin α · sin β

• cos (α - β) = cos α · cos β + sin α · sin β

• tg (α + β) = (tg α + tg β) ÷ (1 - tg α · tg β)

• tg (α - β) = (tg α - tg β) ÷ (1 + tg α · tg β)

• ctg (α + β) = (ctg α · ctg β + 1) ÷ (ctg β - ctg α)

• ctg (α - β) = (ctg α · ctg β - 1) ÷ (ctg β + ctg α)

14. Формулы сложения тригонометрических функций.

cos α + cos β = 2cos((α + β)/2) cos((α – β)/2)

cos α – cos β = 2sin((α + β)/2) sin((β – α)/2)

sin α + sin β = 2sin((α + β)/2) cos((α – β)/2)

sin α – sin β = 2sin((α – β)/2) cos((α + β)/2)

tg α + tg β = sin(α + β)/(cos α cos β)

tg α – tg β = sin(α – β)/(cos α cos β)

ctg α ± ctg β = sin(β ± α)/(sin α sin β)

15. Формулы приведения. Формулы двойных и половинных углов.

Формулы приведения

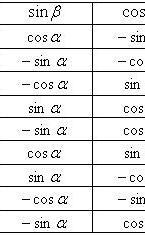
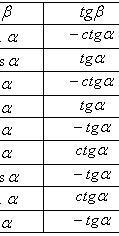
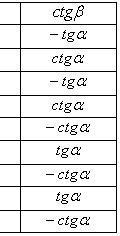
Формулы двойного угла

• cos 2α = cos² α - sin² α

• cos 2α = 2cos² α - 1

• cos 2α = 1 - 2sin² α

• sin 2α = 2sin α · cos α

• tg 2α = (2tg α) ÷ (1 - tg² α)

• ctg 2α = (ctg² α - 1) ÷ (2ctg α)

Формулы половинных углов

16. Свойства и график тригонометрической функции y=Sin x.

Графики и свойства тригонометрических функций

График функции y = sin(x).

Синусом числа х (sin x) называется ордината точки тригонометрического круга, полученной поворотом точки (1;0) на х рад против часовой стрелки.

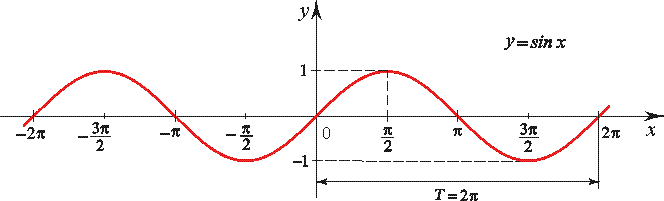
Основные свойства функции y = sin(x).

1. Областью определения функции является множество всех действительных чисел: 2. Областью значений функции является множество значений всех чисел отрезка на интервале [−1;1], значит, синус — функция ограниченная.

3. Функция нечетная: . График нечетной функции симметричен относительно начала координат — точки О.

4. Функция периодическая с наименьшим положительным периодом T = 2π: .

5.
6.
7.

8. Функция возрастает от −1 до 1 на промежутках:

9. Функция убывает от 1 до −1 на промежутках:

10. Наибольшее значение sin x = 1 функция приобретает в точках:

11. Наименьшее значение sin x = −1 функция приобретает в точках:

17. Свойства и график тригонометрической функции y= ctg x.