19.Ср. Возможная ошибка выборочной средней и выборочной доли. Факторы, опред-ие ее величину. Порядок расчета средней возможной ошибки.

Каждая выборка V=n – малых ед-ц из генеральной совокупности V=N –ед-ц имеет свои значения средней x и значение доли w , кот. отличаются от этих же характеристик по генеральной совокупности Х и W. Разница между выборочными харак-ми и их значениями генеральной совокупности – ошибка выборки. Эти ошибки в одних выборках будут больше, а в др. меньше по величине. Число всех возможных выборок объемом n ед-ц из генеральной совокупности N ед-ц опред-ся величиной сочетаний из N ед-ц по n элементов С ⁿ_N=N!/n!(N-n)!

Сочетания- это такие соеденения элементов, кот. отличаются только составом элементов. Если рассматривать все возможные выборки объемом n ед-ц из генеральной совокупности N ед-ц, то из всего множества их ошибок можно рассчитать среднюю возможную ошибку выборки. Она рассчитывается в форме квадратичной средней величины. Величина средней возможной ошибки определяется: 1) вариацией признака б^2, 2) объемом выборки –n 3) долей отбора d=n/N. Средняя возможная ошибка выборки для средней.

Ср. возможная ошибка выборки

Для средней

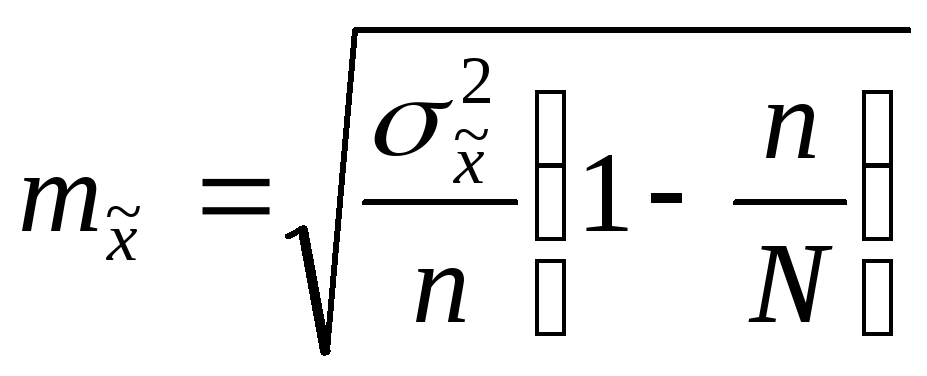
Средняя возможная ошибка выборки для доли ; (1-n/N) – коэффициент бесповторности.

20.Предел ошибка выборки и определяющие ее факторы. Оценка показателей генеральной совокупности по рез-татам выборочного наблюдения.

В реальности мы располагаем рез-ми одного конкретного выборочного наблюд-я и по его рез-ам необходимо опред-ть знач-я изучаемых хар-к в ген совок-ти, а так же оценить надежность полученных результ-ов. Для этого необходимо знать:1) наибольшую вел-ну ош, кот может встретиться в любой из всех возможных выборок данного объема.2) знать вероятность появления этой максим вел-ны. Пред. ош выборки опред-ет наибольшую вел-ну ош, кот. не м.б. превышена в выборках данного объема и это событие можно соблюдать с опред-ной вероятностью, т.е. для строго установленных частей всех возможных выборок для данного объема. В мат стат-ке устанав-ся зависимость пред ош выборки от вел-ны сред возможной ош и от вероятности проявления пред ош-ки: (для выборочной средней)

Предельная ошибка для выборочной доли

(для доли)

Пред ошибка связанна с вероятн-ю ее проявления через коэф-т доверия =t. Чем больше t, тем больше предельная ошибка по сравнению со средней возможной ошибкой. Мат стат-ка установила: вероятность события, при кот значение предельной ошибки будет нах-ся в определ границах описывается интегралом вероятности Муавра Лапласа, а распределение ошибок выборки подчиняется закону норм-го распред-ния. Если предельная ошибка мала и составляет от +m до -m, т.е. t = 0, то вер-ть попадания фактической ош в эти границы мала = 68,3%. Делаем границы больше – вероятность возрастает.Т.о. чем шире граница, в кот. Нах-ся предельн ошиб, тем больш вероятность того, что фактич ошиб выборки попадет в эти границы. Т.о., д/каждого конкретного t рассчитаны значения соответствующей вероятности. Значения вероятности показывают, в скольких %, из всех возможных выборок объемом n ед-ц,фактическая ошибка выборки попадет в границы рассчитанных значений предельн ошиб. Фактические ошибки могут выходить за рассчитанные границы=100% - P(t). Зная выборочную среднюю долю и их предельные ошибки, можно найти доверительные интервалы для значения генеральн средней и генер доли. Чем выше вероятность оценки генр хар-к,тем шире границы доверит интервалов и ниже точность оценки. Поэтому следует разумно определять надежность границ оценки. Если известен объем генеральной совокупности и возможные значения генеральной средней и генеральной доли оценки с помощью доверит-ых интервалов, тогда можно определить границы для общего объема признака по генер совокуп-ти N(x- дельта _x)<=Nx<=N(x+ дельта _x)