
- •Классификация задач оптимизации.
- •При проектировании систем необходимо выполнить комплекс из 8-ми работ
- •Доказательство. Необходимо доказать, что выполняется равенство
- •Пусть дана функция f (х1, х2, …, Хn.) Её градиент:
- •Основная задача.
- •Теорема о крайней точке
- •Доказательство.
- •Пусть задача имеет смешанные ограничения.
- •Получим задачу (2):
- •В симплексную таблицу добавляются 2 столбца-столбцы контрольных сумм. В
- •Предварительный этап:
- •Этап первый
- •Этап второй
- •Этап третий
- •Предназначен для увеличения числа 0 матрицы .
- •Пусть имеется функция
- •Лекция №19.
- •Метод внутриштрафных функций. (Метод барьерных функций)
- •Метод внешних штрафных функций.
Лекция 1. Общие представления М.О.
Задачи на отыскание оптимального решения называются оптимизационными задачами.
-
Но сначала формируем критерий оптимизации, который позволяет судить о том, насколько решение удачно.
-
Затем количественно оценивают принятое решение. Для этого составляем математическое выражение критерия (т.е. зависимость каких-либо величин от факторов).
-
Затем решаем задачу, т.е. оптимизируем критерий.
Применяемые в процессе оптимизации методы называются методами оптимизации.
Определение. Методы оптимизации – это математический аппарат, применяемый при решении задач для нахождения оптимального решения (оптимизационные задачи = экстремальные задачи, т. к. они принимают либо максимальное, либо минимальное значение).
С точки зрения инженерных расчетов М.О. позволяют получить наилучший вариант конструкции, в экономике – наилучшее использование оборудования и т.д.
Общая математическая постановка задач оптимизации.
Оптимизационные задачи, возникающие в результате решения проблем в той или иной области, разнообразны по смыслу и первоначально формируются в содержательных терминах той, области, в которой они решаются. Затем, опираясь на количественные характеристики изучаемого объекта, задача переводится на математический язык. Независимо от того в какой области задача, на математическом языке они имеют одинаковую форму.
(1) f(x1, x2, … xn) – функция n-переменных, которая связывает критерий с параметрами.
Условия, которые
должны выполнятся при нахождении extrem![]() extrem
(max /min).
extrem
(max /min).
(2)
gi
(x1,
x2,
… xn)
--
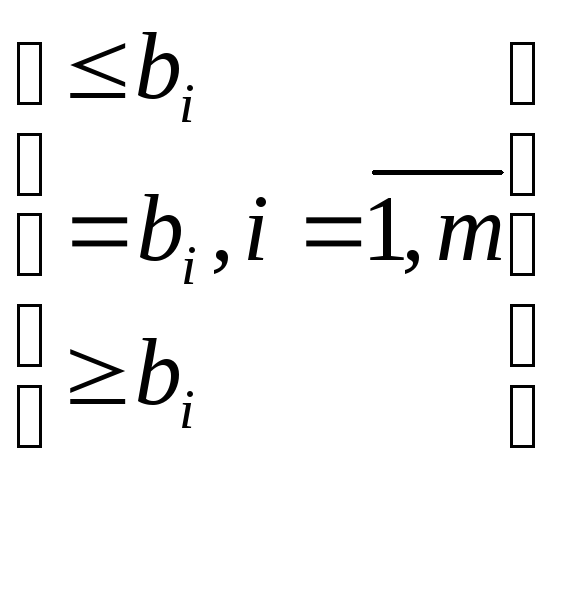
Найти такие значения x1, … , xn при которых функция (1) принимает экстремальные значения при данных ограничениях (2).
Пусть
![]() - решение экстремальной задачи. (T-
транспонированная, 0 – оптимальное)
- решение экстремальной задачи. (T-
транспонированная, 0 – оптимальное)
Решение, которое удовлетворяет системе ограничений, называется допустимым решением. Допустимое решение, при котором функция принимает экстремальное значение называется оптимальным.
Геометрическая интерпретация постановки.
Рассмотрим функцию двух переменных:
D![]() extrem,
gi(x1
,x2).
extrem,
gi(x1
,x2).
 Множество
решений – множество точек, принадлежащих
области D,
если строгое равенство, то точки лежат
на линиях.
Множество
решений – множество точек, принадлежащих
области D,
если строгое равенство, то точки лежат
на линиях.
Надо найти экстремальное значение функции f в этой области D.
Область D может быть пустой, если система ограничений противоречива. В этом случае задача не имеет допустимого решения, следовательно и оптимального.
Предполагаем, что функции непрерывны и существуют производные во всех точках области D.
Классификация задач оптимизации.
1.Задачи
классифицируются по виду функции,
которая может быть функцией или
функционалом. (Функция имеет конечное
число переменных, а функционал -
![]() .
.
2.По виду параметров, входящих в функцию. Различают детерминированные и стахостические задачи
3.Задачи, в которых существуют условия (2), называются задачами условной оптимизации, а если нет, то их называют задачами безусловной оптимизации.
4.В зависимости от класса f и g различают следующие виды задач:
а) если f
и gi
– линейные, т.е. f(x1,
x2,
… xn)=![]() и
g(x1,x2,…xn)–
линейные, то задача линейного
программирования (“программирование”
= “планирование”).
и
g(x1,x2,…xn)–
линейные, то задача линейного
программирования (“программирование”
= “планирование”).
б) если функция f, либо ограничение gi, либо та и другая вместе нелинейны, то – задача нелинейного программирования, т.е. переменные входят с какой-то степенью. Их несколько:
-
Если f и g выпуклые (вогнутые), то задача выпуклого (вогнутого) нелинейного программирования.
-
Если f(x) имеет квадратичную зависимость, т.е.
f(x1,
x2,
… xn)=![]() +
+![]() ,
,
а ограничения
![]() -
т.е. линейны, то задача квадратичного
нелинейного программирования.
-
т.е. линейны, то задача квадратичного
нелинейного программирования.
III. Если f и ограничения g относятся к классу позиномиальной ункции, то задача геометрического программирования:
![]() -
позином, а и с – вещественные числа.
-
позином, а и с – вещественные числа.
VI. Если f относится к сепорабельным функциям, то это задача сепорабельного программирования:
![]() - сепорабельная
функция, т.е. в виде одной переменной.
- сепорабельная
функция, т.е. в виде одной переменной.
5.Если в задаче
оптимизации есть дополнительные
требования на дискретность переменных,
т.е. чтобы переменные принимали только
дискретные значения:![]() ,
,
![]() ,
то это задача дискретного программирования.
Частный случай – задачи целочисленного
программитрования, в которых значения
переменных – целочисленны: 1, 2, 3, ...
,
то это задача дискретного программирования.
Частный случай – задачи целочисленного
программитрования, в которых значения
переменных – целочисленны: 1, 2, 3, ...
6. Если в задаче линейного программирования есть ограничения на переменные целочисленного характера, то это целочисленное линейное программирование.
Лекция 2. Классификация методов оптимизации.
При решении задач оптимизации необходимо правильно выбрать метод оптимизации, необходимо знать основные классы методов оптимизации, но одна и та же задача может быть решена разными методами, следовательно необходимо выбрать подходящий метод оптимизации:
- метод оптимизации функционалов;
- метод оптимизации функций.
1) Используются методы вариационного исчисления, методы основанные на принципе Пантрягина.
2) Методы, связанные с оптимизацией задач, где функция – фукциональная зависимость: методы линейной оптимизации и методы нелинейной оптимизации.
Методы линейной оптимизации, применяющиеся при решении задач линейного программирования, называют симплексным методом.
Двойственный симплексный метод.
При решении задач линейного программирования (транспортная задача, задача назначения).
Используется специальные методы.
Методы нелинейной оптимизации, для решения задач нелинейного програмирования:
-
Классический метод математического анализа – для решения задач оптимизации, в которых зависимость целевой функции f(x1.x2….xn) от оптимизизационных параметров задано в явной форме. Оптимальное значение переменных определяется приравниванием к нулю первых производных по всем переменным и решением системы алгебраических уравнений. (1)
Решение системы уравнений только в простейших случаях удается получить аналитически. Дополнительные трудности связаны с тем, что это условие(1) является необходимым условием оптимальности, необходимо полученное решение проверять на достаточность(найти вторую производную – min, max). Метод имеет ограниченное применение. Выбор метода зависит от наличия или отсутствия ограничений.
Методы условной и безусловной оптимизации.
Существует ряд приемов, которые позволяют свести задачу условной оптимизации к безусловной.
Методы условной оптимизации, где есть ограничения, это задача квадратичного программирования.
Методы решения задач квадратичного программирования
-
С использованием процедуры симплексного метода.
-
Приближенные методы.
Методы для решения задач сипарабельного программирования, динамического программирования.
Методы дискретной оптимизации (значения переменных должны быть дискретны):
-
если число переменных небольшое, то для решения задач может быть применим метод полного перебора решений;
-
метод ветвей и границ(нет ограничения на количество переменных);
-
метод динамического программирования;
-
метод целочисленного программирования (переменные должны быть целые(xij)) применяются методы отсечения, в их основе лежат алгоритмы Гомори и их модификации.
Для решения задач стохастического программирования применяются методы основанные на апроксимизации детерминирования.
Применение МО на этапе проектирования системы.
Обычно при проектировании систем выделяют 3 уровня оптимизации:
1-ый: уровень выбора идей и принципов действия проектируемой системы.
На этом уровне используются методы, базирующиеся на эвристическом программировании.
2-ой: уровень структурной оптимизации системы.
Т.е. поиск наилучшей структуры проектируемой системы. Под структурой системы понимается набор составляющих ее элементов и связи между ними. Структура определяет, как устроена система, из каких частей она состоит, как эти части связаны между собой. Под оптимальной структурой понимается такой вариант структуры, который удовлетворял бы всем симплексным, технологическим, конструктивным, экономическим требованиям. В качестве критерия оптимальной структуры может выступать стоимость, или надежность, или вес системы и т. п.
Также должны быть какие-то ограничения. Задача сводится к отысканию наименьшего значения функции ( критерия), которая характеризует функцию системы. Задача поиска оптимальной системы сводится к комбинаторной задаче, которая может быть сведена к задаче дискретного программирования.
3-ий: параметрическая оптимизация.
Задача параметрической оптимизации состоит в определении наилучших значений параметров системы для выбранной структуры с учетом всех требований на проектируемую систему. Надо найти экстремальное значение функции, зависящей от параметров системы с учетом ограничений на параметры.
Для решения таких задач используются методы нелинейного программирования. При решении задач оптимизации с дискретными значениями параметров используются методы целочисленного программирования.
Применение МО в процессе функционирования автоматизированных и информационных систем.
МО в процессе функционирования систем являются аппаратом планирования и управления, т.е. являются основой решения типовых и специфических задач, решаемых той или иной автоматизированной системой.
Пример. На каждом предприятии существует АСУ. Типовая АСУ состоит из подсистем.
Рассмотрим их технико-экономическое планирование, где рассматривается задача оптимального распределения годовой производственной программы по месяцам. Задача оптимального распределения заключается в обеспечении равномерной загрузки оборудования, площадей и рабочих по месяцам. При этом должны быть учтены директивные сроки выпуска продукции в заданном объеме и заданной номенклатуры. Распределение производственной программы осуществляется с учетом имеющегося оборудования, площадей, рабочих, материальных и сырьевых ресурсов. От того, как составлена программа, зависит недогрузка и перегрузка площадей; недогрузка приведет к простою площадей и уменьшению выпуска продукции, перегрузка приведет к выходу из строя оборудования, потерям от брака, уменьшению выпусков продукции.
В качестве критерия оптимальности берется годовая прибыль предприятия, рентабельность и приведенные затраты. При решении задачи используются методы линейного программирования.
Применение методов оптимизации в процессе проектирования и функционирования автоматизированных и информационных систем.
Проектирование систем представляет собой комплекс сложных дорогостоящих мероприятий, рассредоточенных во времени и проводимых в условиях ограниченности выделенных ресурсов(материальных, трудовых, денежных и так далее).
Пример.
