15. Модели управления запасами. Основные понятия.

Спрос на запасы м б детерминирован. Случайность м б описана случайным V S в детерминированным моментом времени. Пополнение склада ( периодически; по мере исчерпания запаса)

V запаса – заказ подается на одну и ту же величину при достижении заказа заданного уровня( точка заказа)

Время доставки – заданное пополнение поступает на склад мгновенно

Стоимость поставки (разовые затраты не зависящие от V партии; затраты, которые линейно зависят от V партии)

Издержки хранения: что за хранение каждой единицы товара в единицу времени снимается определенная плата.

Штраф за дефицит: убытки связанные с отсутствием запаса в нужный момент времени

Номенклатура запаса: хранение на складе однотипных товаров

Структура складной системы: модели одиночного склада.

В качестве критерия эффективности управления запасами выступает функция затрат, которые п с сумму затрат на хранение, поставку и затраты на штраф. В моделях используется a(t), b(t), r(t) по времени и называются интенсивности наполнения по S, если они не являются случайными, то модель – детерминированная, а если одна из них носит случайный характер – стахастическая.

Статическая модель используется при принятии разовых решений об уровне запаса

Динамическая – о принятии последовательных решений. Уровень запасов во времени определяется основным уравнением запасов:

Y(t)=Y₀+A(t)-B(t)

16.Статическая детерминированная модель управления запасами без дефицита

Пусть общее потребление запасаемого продукта за рассматриваемый интервал времени . b(t) = b= const.

Интенсивность расходования запасов b=(n объем партии).

Время, за которое будет использована вся партия T=. Если отсчет времени начать с момента поступления первой партии, то уровень запаса в начальный момент равен объему этой партии. I(0)=n I(t)=n-bt

Задача управления запасами состоит в определении такого объема партии n, при котором суммарные затраты на создание и хранение запаса были бы минимальными.

Пусть С-суммарные зараты, С₁-затраты на создание запаса, С₂-затраты на хранение запаса.

Пусть затраты на доставку одной партии продукта независимые от объема партии – С₁, а затраты на хранение первой единицы продукта в единицу времени = С_2. К-число партий.

К=, C₁=c₁k=c₁

Средний запас за промежуток [0;T] =, т.е. затраты на хранение всего запаса при линейном(по времени) его расходе равны запасам на хранение среднего запаса.

Учитывая периодичность функции I(t) и затраты хранения запаса за промежуток времени

С₂===

C=

C’(n)=

n=n₀= n₀= - оптимальный объем партии, формула Уилсона

17.Статическая детерминированная модель управления запасами с дефицитом

Необходимость покрытия дефицита => мах уровень запаса S в момент поставки каждой партии не равен объему n, а меньше его на величину дефицита n-S, накопившегося за время T

T=

В данной модели функцию суммарных затрат наряду с затратами С₁ и С₂ необходимо ввести С₃ – штраф из-за дефицита.

С=С₁+С₂+С₃ С₂===

При расчете затрат С₃ будем считать, что штраф за дефициты составляет единицу времени t₃ на каждую единицу продукта.

Так как средний уровень за период T₂=, то штраф за период T₂₌, тогда штраф за весь период

С₃=0,5С₃(n-S)T₂k=0,5C₃(n-S))T=

Формула суммарных затрат

С=С₁+C₂+

Рассматривая задачу управления запасами сводится к описанию такого объема партии и мах уровня запаса Ы, при котором функция С принимает min значения.

Решая систему получаем формулу наиболее экономичного объема партии и maх уровень запаса для модели с дефицитом

n₀₌

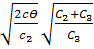
S₀=₌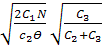

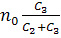
Р=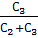

Если С₃ мало по сравнению с C₂, то величина плотности убытков из-за неудовлетворенного спроса близка к 0, когда С₃ значительно превосходит С₂, то р->1

n₀=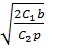S₀=n₀+p