Формула Остроградского – Лиувилля.

Рассмотрим линейное однородное уравнение

.

Определитель Вронского можно вычислить по формуле Остроградского – Лиувилля

.

Вывод формулы Остроградского – Лиувилля.

Известна формула для производной определителя

.

Вычислим ...+

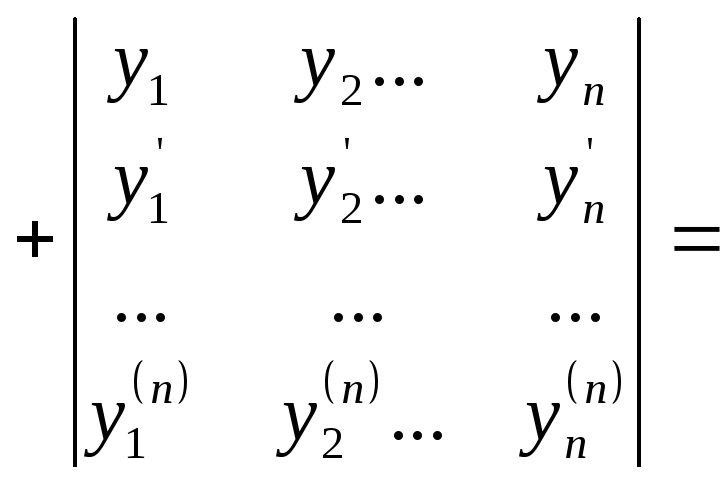
0+...+0+ .

, .

Замечание. В формуле Остроградского – Лиувилля участвуют только коэффициенты при двух старших производных.

Рассмотрим частный случай уравнения второго порядка.

. Здесь формулу Остроградского – Лиувилля можно вывести проще. Рассмотрим - два частных решения

. , . Умножим первое уравнение на , а второе на и вычтем первое уравнение из второго.

.

Так как , то = .

Теперь уравнение можно переписать в виде . Решая это уравнение с разделяющимися переменными, получаем формулу Остроградского – Лиувилля

Формула для построения второго частного решения по известному

(построение фундаментальной системы).

.

Разделим обе части уравнения на

.

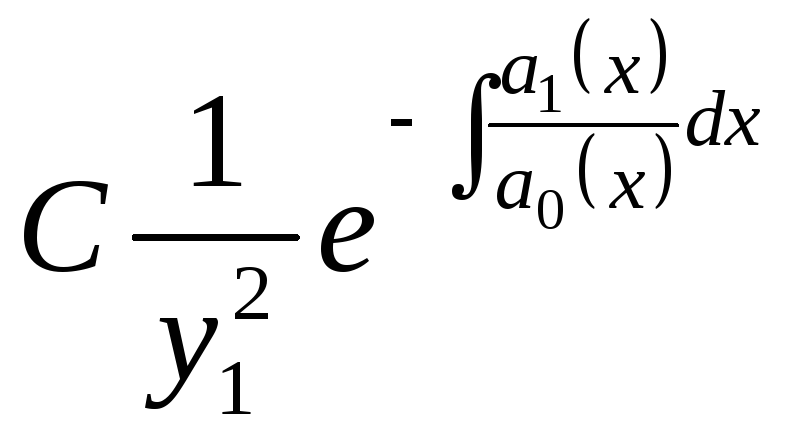
Отсюда . Нам надо найти частное решение, поэтому выберем С=1, C ₁=0, получим .

Билет 13

Лекции 15–16. Линейные дифференциальные уравнения n –ого порядка с переменными коэффициентами.

Линейное однородное дифференциальное уравнение n –ого порядка с переменными коэффициентами может быть записано в виде

Линейное неоднородное дифференциальное уравнение n –ого порядка с переменными коэффициентами может быть записано в виде

.

Если коэффициенты и правая часть – непрерывные функции и , то условия теоремы Коши выполнены, решения однородного и неоднородного уравнений существуют и единственны.

Введем линейный дифференциальный оператор

Здесь обозначает оператор дифференцирования .

Тогда линейное однородное уравнение можно записать в виде , а линейное неоднородное – в виде .

Так как линеен, то

.

Пользуясь линейностью оператора, легко доказать теоремы о свойствах решений однородного и неоднородного уравнений (ниже обозначено - решение однородного уравнения, - решение неоднородного уравнения).

Теоремы о свойствах решений.

1. сумма или разность решений однородного уравнения есть решение однородного уравнения,

2. разность решений неоднородного уравнения есть решение однородного уравнения,

3. сумма решений однородного и неоднородного уравнений есть решение неоднородного уравнения.

Докажем эти теоремы.

1. 

2. 

3. .

Билет 14

Формула для построения второго частного решения по известному

(построение фундаментальной системы).

.

Разделим обе части уравнения на

.

Отсюда . Нам надо найти частное решение, поэтому выберем С=1, C ₁=0, получим .

Билет 15

Линейная зависимость и независимость.

Функции называются линейно независимыми, если

(допустима только тривиальная линейная комбинация функций, тождественно равная нулю). В отличие от линейной независимости векторов здесь тождество линейной комбинации нулю, а не равенство. Это и понятно, так как равенство линейной комбинации нулю должно быть выполнено при любом значении аргумента.

Функции называются линейно зависимыми, если существует не нулевой набор констант (не все константы равны нулю) , такой что (существует нетривиальная линейная комбинация функций, тождественно равная нулю).

Теорема. Для того чтобы функции были линейно зависимы, необходимо и достаточно, чтобы какая-либо из них линейно выражалась через остальные (представлялась в виде их линейной комбинации).

Докажите эту теорему самостоятельно, она доказывается так же, как аналогичная ей теорема о линейной зависимости векторов.