12.Производная функции, ее геометрический смысл.
Уравнение касательной и нормали к плоской кривой. Производные
основных элементарных функций. Таблица производных.
Определение. Производной функции f(x) в точке х = х0 называется предел отношения приращения функции в этой точке к приращению аргумента, если он существует.
у
f(x)
f(x0 +x) P
f
f(x0) M
x
0 x0 x0 + x x
Пусть
f(x)
определена на некотором промежутке (a,
b).
Тогда
тангенс угла наклона секущей МР к графику
функции.
,
где - угол наклона касательной к графику функции f(x) в точке (x0, f(x0)).
Угол между кривыми может быть определен как угол между касательными, проведенными к этим кривым в какой- либо точке.
Уравнение
касательной к кривой:
Уравнение
нормали к кривой:
.
Фактически производная функции показывает как бы скорость изменения функции, как изменяется функция при изменении переменной.
Физический смысл производной функции f(t), где t- время, а f(t)- закон движения (изменения координат) – мгновенная скорость движения.
Соответственно, вторая производная функции- скорость изменения скорости, т.е. ускорение.
Основные правила дифференцирования.
Обозначим f(x) = u, g(x) = v- функции, дифференцируемые в точке х.
1) (u v) = u v
2) (uv) = uv + uv
3)
,
если v
0
Эти правила могут быть легко доказаны на основе теорем о пределах.
Производные основных элементарных функций.
1)С
= 0; 9)
2)(xm)
= mxm-1;
10)
3)
11)
4)
12)
5)
13)
6)
14)
7)
15)
8)
16)
13.Дифференциал функции. Геометрический смысл дифференциала.
Пусть функция y = f(x) имеет производную в точке х:
Тогда
можно записать:
,
где 0,
при х0.
Следовательно:
.
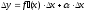Величина x- бесконечно малая более высокого порядка, чем f(x)x, т.е. f(x)x- главная часть приращения у.
Определение. Дифференциалом функции f(x) в точке х называется главня линейная часть приращения функции.
Обозначается dy или df(x).
Из определения следует, что dy = f(x)x или
dy = f(x)dx.
Можно
также записать:
Геометрический смысл дифференциала.
y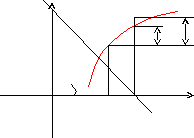
f(x)
K
dy
M y
L
x x + x x
Из треугольника MKL: KL = dy = tgx = yx
Таким образом, дифференциал функции f(x) в точке х равен приращению ординаты касательной к графику этой функции в рассматриваемой точке.
14.Параметрически заданные функции и их дифференцирование. Дифференцирование функции, заданной неявно.
Не
всегда функция бывает
представлена в виде 
.
Например, уравнение 
задает
функцию y,
которую можно из этого уравнения выразить
через 
: 
.
Пусть
переменные 
связаны
между собой некоторым
уравнением
(4.2)
причем y является функцией от x. Тогда говорят, что функция y задана неявно уравнением (4.2).
Не
всегда функции, заданные неявно могут
быть выражены явно через элементарные
функции. Так, из уравнения 
,
которое неявно задает функцию y,
нельзя выразить y явно
через элементарные функции.
Для того чтобы найти производную y' для функции, заданной неявно уравнением (4.2) надо найти производные по x от обеих частей этого уравнения, помня, что y – функция от x и приравнять эти производные. Из полученного уравнения найти y'.
Пример
4.2. Найти
производную функции, заданной неявно
уравнением 
.
Решение.
.
.
Отсюда 
.
4.3. Дифференцирование функций, заданных параметрически
Рассмотрим задание линии на плоскости, при котором переменные x, y являются функциями третьей переменной t (называемой параметром):
(4.3)
Каждому
значению t из
некоторого интервала соответствуют
определенные значения x и y,
а, следовательно, определенная
точка M
плоскости.
Когда t пробегает
все значения из заданного интервала,
то точка M
описывает
некоторую линию L.
Уравнения (4.3) называютсяпараметрическими уравнениями
линии L.
Если
функция 
на
некотором интервале изменения t имеет
обратную функцию 
,
то подставляя это выражение в уравнение 
,
получим 
,
которое задает y как
функцию от x.
Пусть 
, 
имеют
производные, причем 
.
По правилу дифференцирования сложной
функции 
.
На основании правила дифференцирования
обратной функции 
,
имеем:
(4.4)
Полученная формула (4.4) позволяет находить производные для функций, заданных параметрически.
Пример 4.3. Пусть функция y, зависящая от x, задана параметрически:
.
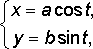
Найти 
.
Решение.
Пример
4.4. Найти 
,
если переменные 
и 
связаны
соотношением
.
Решение.
Явно выразить одну из переменных через другую невозможно, поэтому находим производные левой и правой частей данного равенства и приравниваем их:
.
Далее имеем:
;
.
Перенося
слагаемые, содержащие 
,
в одну часть равенства, вынося 
за
скобку, а остальные слагаемые – в другую
и деля на коэффициент при 
,
получаем:
.
Пример
4.5. Найти 
и 
для
функции, заданной параметрически:
.
Решение
;
;
;
;
;
.
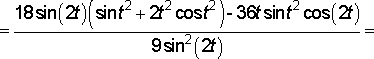
Рассмотрим
показательно-степенную функцию 
,
где 
, u(x), v(x)
– дифференцируемые функции.
Прологарифмируем
равенство 
,
получим: 
(по
свойствам логарифмов). Дифференцируем
обе части полученного равенства как
неявную функцию, помня, что y –
функция от x:
,
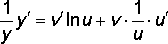откуда 
.
Подставляя
сюда 
,
имеем:
.
Этот прием нахождения производной называется логарифмическим дифференцированием.
Пример
4.6. Найти 
.
Решение.
Вначале прологарифмируем данное равенство
,
и найдем производные от обеих частей полученного равенства, приравнивая их:
Учитывая,
что 
,
имеем:
.
Пример
4.7. 
,
(x
> 0). Найти
производную функции y'.
Решение.
,
или 
5.1. Понятие производной высшего порядка
Пусть
функция
определена
и дифференцируема на некотором
промежутке X,
тогда ее производная 
также
является функцией от x на
этом промежутке. Если 
имеет
производную на промежутке X,
то эта производная называется производной
второго порядка функции y
= f(x)
и обозначается: y'' или 
.
Итак, 
Производная
от производной второго порядка
называется производной
третьего порядка и
обозначается: y''' или 
.
Вообще, производной
n-го порядка называется
производная от производной 
-го
порядка и обозначается: y(n) или f (n)(x).
Итак,
f (n)(x) = (f (n-1)(x))'.
Производные y'', y''', ... называются производными высших порядков.
Пример
5.1. 
.
Найти 
и 
.
Решение.
= 
=
,
=
–
,
= 
= 
,
= 
= 
= 
.
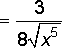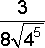Пример
5.2. Найти
производную n-го
порядка для функции 
.
Решение.
,
,
.
По
аналогии находим: 
.
5.2. Производные высших порядков от функций, заданных параметрически
Пусть функция y, зависящая от x, задана параметрически на интервале Т:
, 
Найдем 
.
Известно, что 
= 
= 
(п.
4.3), поэтому
= 
= 
= 
= 
.
Аналогично
будет вычисляться 
и
т. д.
Пример
5.3. Найти 
и 
для
функции, заданной параметрически:
.
Решение.
;
;
;
;
;
=
.
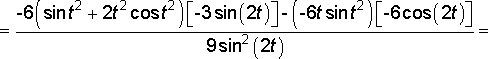