
- •Раздел «линейная и векторная алгебра»
- •1.Основные алгебраические структуры: группа, кольцо, поле.
- •2.Определители 2-го, 3-го, n-го порядков, их свойства, способы вычисления.
- •3.Алгебраические дополнения и миноры. Правило Крамера.
- •4.Матрицы, линейные операции над ними и их свойства. Умножение матриц.
- •5.Понятие обратной матрицы. Необходимое и достаточное условие ее существования и методы вычисления.
- •6.Понятие n-мерного векторного пространства.
- •7.Ранг матрицы, его вычисление. Теорема Кронекера-Капелли.
- •8.Теорема о базисном миноре.
- •9.Проекция вектора на ось, свойства проекций. Направляющие косинусы.
- •10.Векторы, линейные операции над ними. Длина вектора. Линейная зависимость
- •11.Скалярное произведение векторов, его свойства и выражение через
- •12. Векторное произведение векторов, его свойства и выражение через
- •13. Смешанное произведение векторов, его свойства и выражение через
- •2. Раздел «аналитическая геометрия»
- •1.Понятие об уравнении линии и поверхности. Полярная система координат.
- •2. Уравнение прямой линии на плоскости: общее, с угловым коэффициентом,
- •3. Общее уравнение плоскости в пространстве, расстояние от точки до
- •4. Различные формы уравнения прямой в пространстве (канонические,
- •5. Кривые второго порядка: окружность, эллипс, гипербола, парабола,
- •Кривая второго порядка может быть задана уравнением
- •6. Уравнения поверхности в пространстве. Цилиндрические
- •7. Преобразование координат: поворот и параллельный перенос,
- •1. Прямоугольные координаты точки на плоскости
- •Т.Е. Новые координаты точки м(х'у') равны ее старым координатам минус координаты нового начала. Обратно, из (1.1.1) находим
- •3. Введение в математический анализ
- •1. Числовые множества. Ограниченные и неограниченные множества. Верхние и нижние грани множества. Предельные точки множества.
- •2.Предел числовой последовательности. Единственность предела.
- •3. Понятие функции, способы ее задания. Сложные функции.
- •4. Односторонние пределы. Ограниченность функции, имеющей предел.
- •5. Бесконечно малые функции и их свойства. Произведение
- •6. Предел суммы, произведения и частного функции.
- •7. Первый замечательный предел.
- •8.Второй замечательный предел. Число "е".
- •9.Сравнение бесконечно малых функций. Эквивалентные бесконечно малые. Замена бесконечно малых эквивалентными при вычислении пределов.
- •10.Непрерывность функции. Непрерывность основных элементарных функций. Точки разрыва функции и их классификация.
- •11.Непрерывность функции на отрезке. Свойства непрерывных на отрезке функций: ограниченность, существование наибольшего и наименьшего значений, существование промежуточных значений.
- •12.Производная функции, ее геометрический смысл.
- •13.Дифференциал функции. Геометрический смысл дифференциала.
- •14.Параметрически заданные функции и их дифференцирование. Дифференцирование функции, заданной неявно.
- •15.Теоремы Ферма, Ролля, Лагранжа.
- •16.Раскрытие неопределенностей, правила Лопиталя.
- •17.Условие возрастания и убывания функций. Точки экстремума. Отыскание наибольших и наименьших значений непрерывной на отрезке функции.
- •18. Исследование функций на выпуклость и вогнутость. Асимптоты кривой. Общая схема построения графика.
- •4. Функции многих переменных
- •1.Понятие метрического пространства. Открытые и замкнутые множества.
- •2.Функции многих переменных. Частные производные и полный дифференциал ф.М.П.
- •3.Дифференцирование сложных ф.М.П. Производная по направлению.
- •4.Касательная плоскость и нормаль к поверхности. Частные производные высших порядков.
- •5.Экстремумы ф.М.П. Достаточное условие экстремума.
5. Бесконечно малые функции и их свойства. Произведение
бесконечно малых функций. Частное от деления бесконечно малой
функции на функцию, имеющую предел, отличный от нуля.
Определение.
Функция f(x)
называется бесконечно
малой
при ха,
где а может быть числом или одной из
величин ,
+
или -,
если
 .
.
Бесконечно малой функция может быть только если указать к какому числу стремится аргумент х. При различных значениях а функция может быть бесконечно малой или нет.
Пример.
Функция f(x)
= xn
является бесконечно малой при х0
и не является бесконечно малой при х1,
т.к.
 .
.
Теорема. Для того, чтобы функция f(x) при ха имела предел, равный А, необходимо и достаточно, чтобы вблизи точки х = а выполнялось условие
f(x) = A + (x),
где (х) – бесконечно малая при х а ((х)0 при х а).
Свойства бесконечно малых функций:
-
Сумма фиксированного числа бесконечно малых функций при ха тоже бесконечно малая функция при ха.
-
Произведение фиксированного числа бесконечно малых функций при ха тоже бесконечно малая функция при ха.
-
Произведение бесконечно малой функции на функцию, ограниченную вблизи точки х = а является бесконечно малой функцией при ха.
-
Частное от деления бесконечно малой функции на функцию, предел которой не равен нулю есть величина бесконечно малая.
6. Предел суммы, произведения и частного функции.
Теорема
2.

Теорема
3.

Теорема
4.
 при
при
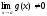
Доказательство теоремы 2. Представим f(x) = A + (x), g(x) = B + (x), где
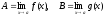 ,
тогда
,
тогда
f(x) g(x) = (A + B) + (x) + (x)
A + B = const, (х) + (х) – бесконечно малая, значит

Теорема доказана.
Доказательство теоремы 3. Представим f(x) = A + (x), g(x) = B + (x), где
 ,
тогда
,
тогда
AB = const, (х) и (х) – бесконечно малые, значит

Теорема доказана.
Доказательство:
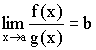
![]()
Из теоремы о связи между пределом и бесконечно малой величиной следует:

![]() ;
;
Получаем: 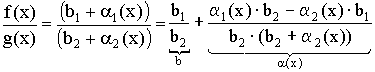
![]()

7. Первый замечательный предел.

![]()
![]()
![]()
![]()
![]()


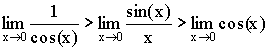
Так
как  ,
то
,
то ![]() .
.
Следствия из теоремы:
1) ![]()
2) ![]()
3) 
4) 
5) ![]()
8.Второй замечательный предел. Число "е".
Доказательство:
Бином Ньютона:
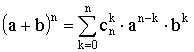 ,
где
,
где  .
.
Используем
бином Ньютона для доказательства
неравенства: 

Отсюда
заключаем, что  ,
а значит
,
а значит  .
.
Следствия из теоремы:
1) ![]()
2) ![]()
3) ![]()
4) 
Число е.
Рассмотрим
последовательность {xn}
=
 .
.
Если последовательность {xn} монотонная и ограниченная, то она имеет конечный предел.
По формуле бинома Ньютона:
 или,
что то же самое
или,
что то же самое

Покажем, что последовательность {xn} – возрастающая. Действительно, запишем выражение xn+1 и сравним его с выражением xn:
 Каждое
слагаемое в выражении xn+1
больше соответствующего значения xn,
и, кроме того, у xn+1
добавляется еще одно положительное
слагаемое. Таким образом, последовательность
{xn}
возрастающая.
Каждое
слагаемое в выражении xn+1
больше соответствующего значения xn,
и, кроме того, у xn+1
добавляется еще одно положительное
слагаемое. Таким образом, последовательность
{xn}
возрастающая.
Докажем теперь, что при любом n ее члены не превосходят трех: xn < 3.
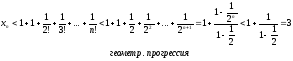
Итак,
последовательность
 -
монотонно возрастающая и ограниченная
сверху, т.е. имеет конечный предел. Этот
предел принято обозначать буквой е.
-
монотонно возрастающая и ограниченная
сверху, т.е. имеет конечный предел. Этот
предел принято обозначать буквой е.

Из
неравенства
 следует, что е
3. Отбрасывая в равенстве для {xn}
все члены, начиная с четвертого, имеем:
следует, что е
3. Отбрасывая в равенстве для {xn}
все члены, начиная с четвертого, имеем:

переходя к пределу, получаем
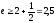
Таким образом, число е заключено между числами 2,5 и 3. Если взять большее количество членов ряда, то можно получить более точную оценку значения числа е.
Можно показать, что число е иррациональное и его значение равно 2,71828…
Аналогично
можно показать, что
 ,
расширив требования к х до любого
действительного числа:
,
расширив требования к х до любого
действительного числа:
Предположим:

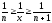


Найдем

Число е является основанием натурального логарифма.
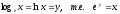

Выше представлен график функции y = lnx.
