4.3.3. Выбор и расчет муфты

Выбор пал на предохранительную фрикционную однодисковую муфту.

Осевое усилие, передаваемое пружиной:

_,

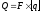_{где F - площадь одной поверхности трения;}

_{q - допускаемое удельное давление.}

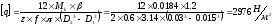
где M_k-крутящий момент на валу;

z - число поверхностей трения;

f - коэффициент трения;

_{β - коэффициент трения при определении расчетного момента.}

D1, D2 - диаметры, ограничивающие рабочие поверхности полумуфт.

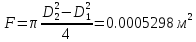
Q = 0.0005298 * 2976 = 1.58 Н.

4.3.4. Расчет пружины

Пружину для муфты выбираем по ГОСТ 13766-86 : позиция 95,

D₁ = 6,5 мм – наружный диаметр пружины,

d = 0.5мм – диаметр проволоки,

с₁ = 2,835 Н/мм – жесткость одного витка,

F₃ = 5,6 Н – сила пружины при максимальной деформации.

Осевое перемещение витка пружины под действием нагрузки:

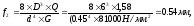
_{где D - средний диаметр пружины,}

_{d - диаметр проволоки,}

_{G-модуль сдвига.}

_{Сжатие или растяжение пружины под действием нагрузки:F2=1,62 мм.}

_{Число рабочих витков:}

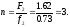
_{Полное число витков пружины:}

Шаг ненагруженной пружины:

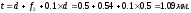
Высота пружины в свободном состоянии:

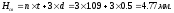
_{Длина пружины под нагрузкой:}

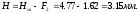
_{Высота пружины сжатой до соприкосновения витков:}

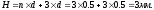
_{Угол подъема витков пружины в свободном состоянии:}

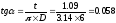
_{α = arctg 0.058 = 3.3град.}

_{Длина развернутой проволоки:}

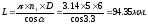
4.3.5. Расчет мальтийского креста

Исходя из условия отсутствия жесткого удара в начале и в конце движения, радиус кривошипа r1 и межосевое расстояние А звязаны зависимостью:

Из технических соображений принимаю радиус кривошипа равным 15.5 мм.

Тогда межосевое расстояние будет равным:

А = 15.5/0.707 = 21.9 мм.

Длина пазов h мальтийского креста определяется из выражения:

h =

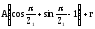
где r = (0.1 .. 0.2)*r₁ / 2 – радиус пальца,

r = 1мм,

Z₁ – количество пазов в кресте.

h = 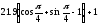= 11мм.

b = 4*r = 4 мм.

Условие прочности на изгиб пальца:

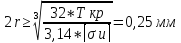
Где 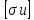= 240 для стали 45

Как видно, условие прочности на изгиб выполняются.

4.4. Силовой расчет.

Крутящий момент на валу двигателя:

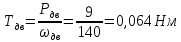
На выходном валу: T₃ = 0.4 Н*м.

На валу-червяке: T₁ = T_дв = 0,064Н*м.

На валу креста: 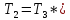η_к* η²_п / i = 0.4*0,9*0.9² / 2.4 = 0.12 Н*м,

Где i – передаточное отношение между кривошипом и крестом,

i = 3.78 / 1.57 = 2,4

4.5. Расчет типовых элементов.

4.5.1. Расчет подшипника.

На основе полученного значения диаметра выходного вала (d = 5 мм), выбираем подшипник радиальный 1006095, параметры которого приведены в таблице2 и таблице 3.

Таблица 2- габаритные размеры подшипника

Размеры, мм
d	D	B
5	13	4

Таблица 3 - Ориентировочные расчётные параметры

Грузоподьёмность, Н
Динамическая (С)	Статическая (С0)
895	336

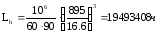
Расчёт подшипника на долговечность:

Теоретическая расчётная долговечность L в млн. оборотов определяется по формуле

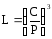
где С - динамическая грузоподъёмность подшипника;

Р - эквивалентная динамическая нагрузка определяется по эмпирическим формулам и зависит от действующих на подшипник сил, характера нагрузки и температуры.

Долговечность подшипника в часах

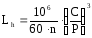
где n - частота вращения кольца подшипника в минуту (n_вых'). Для приборных зубчатых редукторов ресурс работы подшипников устанавливается в пределах 1000-10000 ч.

Эквивалентная динамическая нагрузка Р для однорядных радиальных и радиально-упорных шарикоподшипников

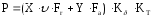
где К_δ - коэффициент, учитывающий влияние динамических условий работы (К_δ = 1);

К_Т - коэффициент, учитывающий влияние температурного режима работы на долговечность подшипника (К_Т = 1);

ν - коэффициент, учитывающий какое кольцо вращается; при вращении внутреннего кольца ν = 1; наружного кольца ν = 1.2 .

X – коэффициент радиальной нагрузки (для радиально-упорного однорядного подшипника = 0,5),

Y – коэффициент осевой нагрузки (для радиально-упорного однорядного подшипника с углом контакта 12⁰ = 0,47),

F_r - радиальная нагрузка;

F_a - осевая нагрузка.

Радиальная нагрузка определяется, как наибольшая величина, полученная из следующих уравнений

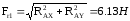
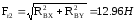
Эквивалентная статическая нагрузка P₀ для радиальных, радиально-упорных шарикоподшипников выбирается как наибольшая величина, полученная из уравнений.

Поскольку 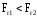, то

F_r = F_r1 = 12.96 Н

Определим эквивалентную динамическую нагрузку по формуле

Номинальная долговечность:

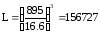млн.об.

или