
- •Билет 1
- •Теорема об оценке определенного интеграла.
- •Теорема о среднем значении определенного интеграла («теорема о среднем»).
- •Нормальные системы дифференциальных уравнений.
- •2 Метод вариации произвольной постоянной.
- •Дифференциальные уравнения первого порядка.
- •2Система линейных дифференциальных уравнений с постоянными коэффициентами может быть записана в виде
- •Рассмотрим случай, когда все собственные значения линейного оператора с матрицей a (или все характеристические числа матрицы a, что одно и то же) действительны и различны.
- •Линейная зависимость и независимость.
- •Свойства определенного интеграла.
- •Метод подбора формы частного решения.
- •Пусть правая часть представляет собой квазиполином .
- •Свойства определенного интеграла.
- •Метод подбора формы частного решения.
- •Свойства определенного интеграла.
- •Формула для построения второго частного решения по известному
- •Интеграл с переменным верхним пределом.
- •Линейные дифференциальные уравнения с постоянными коэффициентами.
- •Метод вариации произвольной постоянной.
Метод подбора формы частного решения.
Рассмотрим сначала уравнение второго порядка
![]() Пусть
правая часть представляет собой
квазиполином
Пусть
правая часть представляет собой
квазиполином
![]() .
Ищем частное решение в виде
.
Ищем частное решение в виде
![]() .
Здесь
.
Здесь
![]() - полином n-ой
степени,
- полином n-ой
степени,
![]() -
полином, степень которого надо определить.
-
полином, степень которого надо определить.
![]() ,
,
![]() .
.
![]()
а)
Если
![]() - не корень характеристического
уравнения, то
- не корень характеристического
уравнения, то
![]() ,
и многочлен
,
и многочлен
![]() надо выбирать той же степени, что и
надо выбирать той же степени, что и
![]() ,
т.е. степени n.
,
т.е. степени n.
б)
Если
![]() - простой корень характеристического
уравнения, то
- простой корень характеристического
уравнения, то
![]() .
В этом случае многочлен
.
В этом случае многочлен
![]() надо выбирать той же степени, что и
надо выбирать той же степени, что и
![]() ,
т.е. степени n.
Тогда степень многочлена надо выбирать
равной n+1.
Однако при дифференцировании
,
т.е. степени n.
Тогда степень многочлена надо выбирать
равной n+1.
Однако при дифференцировании
![]() производная свободного члена (постоянной)
равна нулю, поэтому
производная свободного члена (постоянной)
равна нулю, поэтому
![]() можно выбирать в виде
можно выбирать в виде
![]() =
=![]() .
.
в)
Если
![]() - кратный корень характеристического
уравнения, то
- кратный корень характеристического
уравнения, то
![]() .
В этом случае многочлен
.
В этом случае многочлен
![]() надо выбирать той же степени, что и
надо выбирать той же степени, что и
![]() ,
т.е. степени n.
Тогда степень многочлена
,
т.е. степени n.
Тогда степень многочлена
![]() надо выбирать равной n+2.
Однако при двукратном дифференцировании
надо выбирать равной n+2.
Однако при двукратном дифференцировании
![]() производная не только свободного члена
равна нулю, но и производная линейного
члена равна нулю. Поэтому
производная не только свободного члена
равна нулю, но и производная линейного
члена равна нулю. Поэтому
![]() можно выбирать в виде
можно выбирать в виде
![]() =
=![]() .
.
Пример.
![]()
![]() ,
,
![]()
![]() ,
,
![]() - не корень характеристического
уравнения, поэтому частное решение
надо искать в том же виде, что и правая
часть,
- не корень характеристического
уравнения, поэтому частное решение
надо искать в том же виде, что и правая
часть,
![]() .
Подставляем в неоднородное уравнение
с правой частью
.
Подставляем в неоднородное уравнение
с правой частью
![]() .
.
![]()
![]() .
.
![]() .
Корень
.
Корень
![]() содержится один раз среди корней
характеристического уравнения, поэтому
частное решение ищется в виде
содержится один раз среди корней
характеристического уравнения, поэтому
частное решение ищется в виде
![]() .
Подставляем в неоднородное уравнение
с правой частью
.
Подставляем в неоднородное уравнение
с правой частью
![]() .
.
![]()
![]() .
Суммируя оба частных решения, получаем
частное решение неоднородного уравнения
для исходной правой части:
.
Суммируя оба частных решения, получаем
частное решение неоднородного уравнения
для исходной правой части:
![]() .
Общее решение неоднородного уравнения
будет
.
Общее решение неоднородного уравнения
будет
![]() .
.
2)
Правая часть имеет вид
![]()
-
Если
 не корни характеристического уравнения,
то частное
решение ищется в том виде, в котором
задана правая часть:
не корни характеристического уравнения,
то частное
решение ищется в том виде, в котором
задана правая часть:
![]() ,
,
где
![]() - полиномы степени m
– максимальной из степеней полиномов
- полиномы степени m
– максимальной из степеней полиномов
![]() .
.
б)
Если
![]() -
пара корней характеристического
уравнения,
то частное решение ищется в виде
-
пара корней характеристического
уравнения,
то частное решение ищется в виде
![]() ,
,
Пример.
![]()
![]()
![]()
![]() Пара корней
Пара корней
![]() =
=![]() - пара корней характеристического
уравнения.
- пара корней характеристического
уравнения.
![]()
 Подставляем в неоднородное уравнение,
получаем
Подставляем в неоднородное уравнение,
получаем
![]() ,
откуда
,
откуда
![]()
![]()
![]() ,
,
![]() Рассмотрим
неоднородное
уравнение n-го
порядка,
покажем, как в нем применять метод
подбора формы частного решения.Здесь
ситуация сложнее, так как в характеристическом
уравнении n
корней, действительные корни и комплексно
сопряженные, простые и кратные корни.
Рассмотрим
неоднородное
уравнение n-го
порядка,
покажем, как в нем применять метод
подбора формы частного решения.Здесь
ситуация сложнее, так как в характеристическом
уравнении n
корней, действительные корни и комплексно
сопряженные, простые и кратные корни.
-
Пусть правая часть неоднородного уравнения имеет вид

-
Если
 не является
корнем характеристического уравнения,
то частное решение неоднородного
уравнения ищется в том же виде, что и
правая часть
не является
корнем характеристического уравнения,
то частное решение неоднородного
уравнения ищется в том же виде, что и
правая часть
 .
. -
Если
 - корень
характеристического уравнения r-ой
кратности,
то частное решение неоднородного
уравнения ищется в виде
- корень
характеристического уравнения r-ой
кратности,
то частное решение неоднородного
уравнения ищется в виде
 .
.
-
Пусть правая часть неоднородного уравнения имеет вид
![]()
а) Если пара комплексно сопряженных корней не является корнями характеристического уравнения, то частное решение неоднородного уравнения ищется в том же виде, что и правая часть
![]() ,
где степень m
многочленов – максимальная из степеней
многочленов
,
где степень m
многочленов – максимальная из степеней
многочленов
![]() .
.
-
Если пара комплексно сопряженных корней является корнями характеристического уравнения r-ой кратности, то частное решение неоднородного уравнения ищется в виде
![]() .Пример.
.Пример.
![]()
![]() ,
,
![]() .
.
![]() .
.
![]() содержится
в корнях характеристического уравнения
2 раза, поэтому
содержится
в корнях характеристического уравнения
2 раза, поэтому
![]() .
Подставляя это частное решение в
неоднородное уравнение с правой частью
.
Подставляя это частное решение в
неоднородное уравнение с правой частью
![]() ,
получим
,
получим
![]()
![]() .
Корни
.
Корни
![]() не
содержатся в корнях характеристического
уравнения, поэтому
не
содержатся в корнях характеристического
уравнения, поэтому
![]() .
Подставляя это частное решение в
неоднородное уравнение с правой частью
.
Подставляя это частное решение в
неоднородное уравнение с правой частью
![]() ,
получим
,
получим
![]() .
.
![]() .
.![]() .
.
![]() +
+![]() .
Пример.
.
Пример.
![]()
![]()
![]() .
.
![]()
![]() содержится
в корнях характеристического уравнения
3 раза, поэтому
содержится
в корнях характеристического уравнения
3 раза, поэтому
![]() .
.
![]() .
Корни
.
Корни
![]() (пара
корней) содержатся в корнях
характеристического уравнения один
раз, поэтому
(пара
корней) содержатся в корнях
характеристического уравнения один
раз, поэтому
![]() .
Неопределенные коэффициенты определяются,
как и выше, подстановкой в уравнение и
сравнением коэффициентов при одинаковых
степенях x,
при sinx,
cosx,
xsinx,
xcosx
.
Неопределенные коэффициенты определяются,
как и выше, подстановкой в уравнение и
сравнением коэффициентов при одинаковых
степенях x,
при sinx,
cosx,
xsinx,
xcosx
Билет 11
1
Формула
Ньютона – Лейбница.Пусть
функция
![]() непрерывна
на отрезке
непрерывна
на отрезке
![]() - некоторая первообразная функции
- некоторая первообразная функции
![]() .
Тогда
.
Тогда
![]() .
.
Доказательство.
Из теоремы о производной интеграла по
переменному верхнему пределу следует,
что
![]() ,
т.е.
,
т.е.
![]() -
первообразная для функции
-
первообразная для функции
![]() .
По теоремам о первообразных две
первообразных отличаются на константу
т.е.
.
По теоремам о первообразных две
первообразных отличаются на константу
т.е.
![]() Но
Но
![]() (свойство 4 определенного интеграла),
поэтому
(свойство 4 определенного интеграла),
поэтому
![]() .
Тогда
.
Тогда
![]() .
Следовательно,
.
Следовательно,
![]() .Формула
Ньютона – Лейбница - это одна из немногих
формул - связок, связывающих различные
разделы математики воедино.
.Формула
Ньютона – Лейбница - это одна из немногих
формул - связок, связывающих различные
разделы математики воедино.
2.
Общее
решение линейного однородного уравнения
есть линейная комбинация решений
фундаментальной системы.![]() .
.
Доказательство.
Покажем, что линейная комбинация
![]() является общим решениям (удовлетворяет
пунктам определения общего решения)
является общим решениям (удовлетворяет
пунктам определения общего решения)
-
 -
решение линейного однородного уравнения
как линейная комбинация решений.
-
решение линейного однородного уравнения
как линейная комбинация решений. -
Зададим произвольные начальные условия
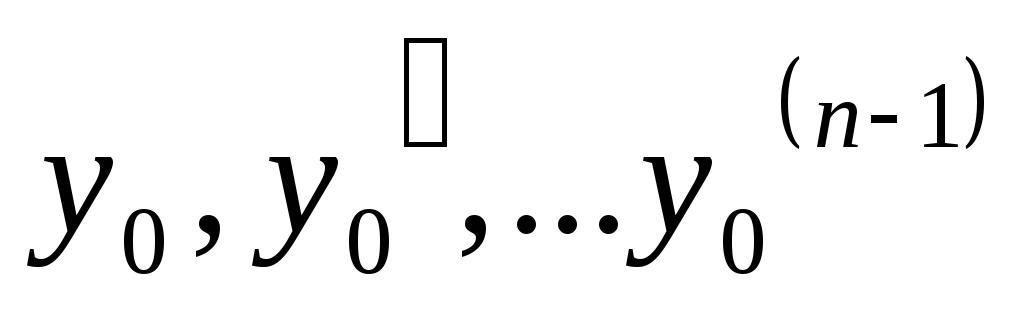 ,
покажем, что можно подобрать константы
,
покажем, что можно подобрать константы
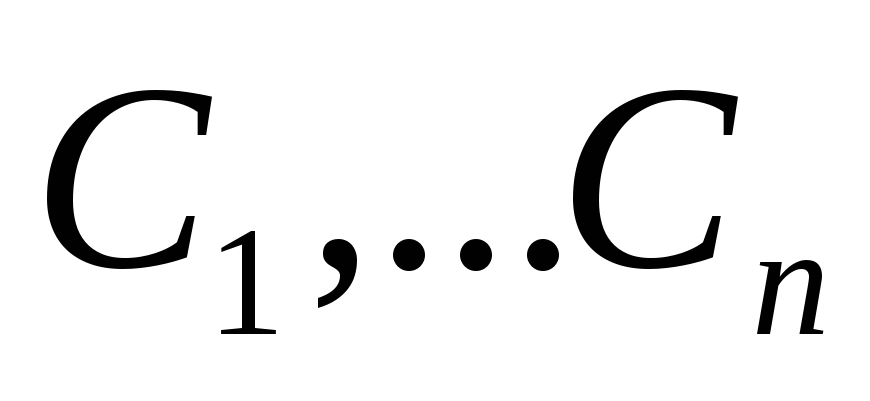 такие, что
такие, что
 удовлетворяет этим начальным условиям.
удовлетворяет этим начальным условиям.
![]()
![]() .
.
![]()
![]() .
.
![]()
![]() .
.
.........................................................................
![]()
![]() .
.
Это
– система линейных алгебраических
уравнений относительно констант
![]() .
Определитель этой системы – определитель
Вронского. Он не равен нулю, так как
решения
.
Определитель этой системы – определитель
Вронского. Он не равен нулю, так как
решения
![]() линейно независимы. Поэтому константы
линейно независимы. Поэтому константы
![]() определяются из этой системы по начальным
условиям – правым частям системы
единственным образом. Следовательно,
определяются из этой системы по начальным
условиям – правым частям системы
единственным образом. Следовательно,
![]() - общее решение.Замечание.
Определитель Вронского (как всякий
определитель) представляет собой
ориентированный n
– мерный объем, натянутый на векторы
решений фундаментальной системы
решений.
- общее решение.Замечание.
Определитель Вронского (как всякий
определитель) представляет собой
ориентированный n
– мерный объем, натянутый на векторы
решений фундаментальной системы
решений.
Формула
Остроградского – Лиувилля. Рассмотрим
линейное однородное уравнение
![]() .
Определитель Вронского можно вычислить
по формуле
Остроградского – Лиувилля
.
Определитель Вронского можно вычислить
по формуле
Остроградского – Лиувилля
![]() .
Вывод формулы Остроградского – Лиувилля.
Известна формула для производной
определителя
.
Вывод формулы Остроградского – Лиувилля.
Известна формула для производной
определителя
 .
.
Вычислим



0+...+0+

![]() .
.
![]() ,
,
![]() .
.
Замечание. В формуле Остроградского – Лиувилля участвуют только коэффициенты при двух старших производных.
Рассмотрим
частный случай уравнения второго
порядка.
![]() .
Здесь формулу Остроградского – Лиувилля
можно вывести проще. Рассмотрим
.
Здесь формулу Остроградского – Лиувилля
можно вывести проще. Рассмотрим
![]() - два частных решения
- два частных решения
![]() .
,
.
,
![]() .
Умножим первое уравнение на y2,
а второе на y1
и вычтем первое уравнение из второго.
.
Умножим первое уравнение на y2,
а второе на y1
и вычтем первое уравнение из второго.
![]() .
.
Так
как
![]() ,
то
,
то
![]() =
=
![]() .
Теперь уравнение можно переписать в
виде
.
Теперь уравнение можно переписать в
виде
![]() .
Решая это уравнение с разделяющимися
переменными, получаем формулу
Остроградского – Лиувилля
.
Решая это уравнение с разделяющимися
переменными, получаем формулу
Остроградского – Лиувилля
![]()
Формула для построения второго частного решения по известному
(построение фундаментальной системы).
![]()
![]() .
Разделим обе части уравнения на
.
Разделим обе части уравнения на
![]()

 .
Отсюда
.
Отсюда
![]()

![]() .
Нам надо найти частное решение, поэтому
выберем С=1, C
1=0,
получим
.
Нам надо найти частное решение, поэтому
выберем С=1, C
1=0,
получим
 .
.
Билет 12
1
Свойства определенного интеграла.
-
Свойства линейности
а)
суперпозиции
![]() ,
,
б)
однородности
![]()
Вообще говоря, свойствами линейности обладают все линейные операции (дифференцирование, интегрирование, проектирование и т.д.)
-
Свойство аддитивности (по множеству)
 Доказательство. Пусть
Доказательство. Пусть
 .
Выберем разбиение так, чтобы точка с
была границей элемента разбиения
.
Выберем разбиение так, чтобы точка с
была границей элемента разбиения
 .
Это возможно (следствие). Составим
интегральную сумму
.
Это возможно (следствие). Составим
интегральную сумму
 .
Будем измельчать разбиение, сохраняя
точку с границей элемента разбиения.
Это возможно (следствие). Тогда предел
при
.
Будем измельчать разбиение, сохраняя
точку с границей элемента разбиения.
Это возможно (следствие). Тогда предел
при
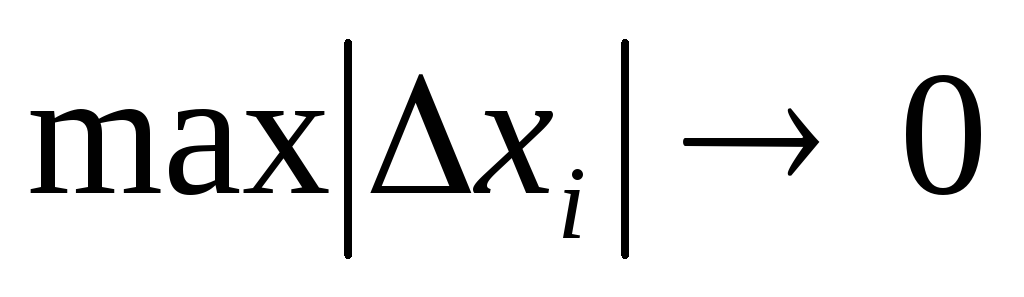 левой
части равенства интегральных сумм
равен
левой
части равенства интегральных сумм
равен
 ,
первого слагаемого правой части
,
первого слагаемого правой части
 ,
второго слагаемого правой части
,
второго слагаемого правой части
 .
. -
 (свойство
«ориентируемости» множества). Составляя
интегральную сумму для интеграла в
правой части равенства, заметим, что
элемент разбиения надо проходить в
другом направлении, от конца отрезка
к началу. Поэтому для этого интеграла
интегральная сумма будет
(свойство
«ориентируемости» множества). Составляя
интегральную сумму для интеграла в
правой части равенства, заметим, что
элемент разбиения надо проходить в
другом направлении, от конца отрезка
к началу. Поэтому для этого интеграла
интегральная сумма будет
![]() -
-
![]() .
Переходя к пределу при измельчении
разбиения, получим
.
Переходя к пределу при измельчении
разбиения, получим
![]() .
.
-
 .
Это постулируется, но, вообще говоря,
это и очевидно.
.
Это постулируется, но, вообще говоря,
это и очевидно. -
 .
.

![]() .
.
-
Если на отрезке
 ,
то
,
то
 .
Так как
.
Так как
 на отрезке, то
на отрезке, то
 .
Переходя к пределу, получим
.
Переходя к пределу, получим
 .
. -
Если на отрезке
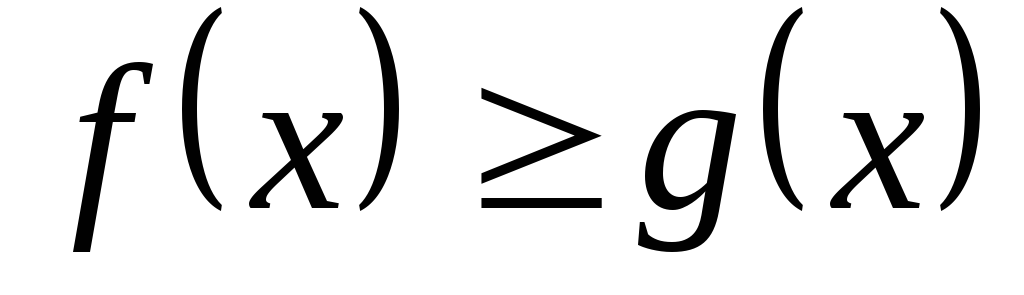 ,
то
,
то
 .
Так как
.
Так как
 на отрезке, то
на отрезке, то
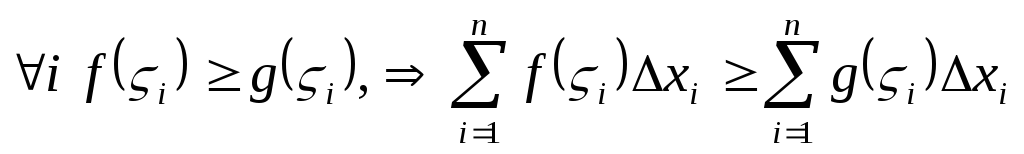 .
Переходя к пределу, получим
.
Переходя к пределу, получим
 .
. -


 .
. -
 (переменная
интегрирования – «немая» переменная,
ее можно изменить, она не несет в себе
самостоятельного смысла)Определенный
интеграл является функцией своих
пределов, при фиксированных пределах
интегрирования это – число. Он определен
своими пределами. Поэтому он и называется
определенным.
(переменная
интегрирования – «немая» переменная,
ее можно изменить, она не несет в себе
самостоятельного смысла)Определенный
интеграл является функцией своих
пределов, при фиксированных пределах
интегрирования это – число. Он определен
своими пределами. Поэтому он и называется
определенным.
2
Метод вариации произвольной постоянной.
Общее
решение однородной системы можно
записать в виде![]() ,
где
,
где
![]() -
фундаментальная матрица системы,
-
фундаментальная матрица системы,
![]() -
вектор произвольных постоянных.
-
вектор произвольных постоянных.
Будем
искать решение неоднородной системы
в том же виде, варьируя вектор произвольных
постоянных:![]()
![]() .Вычисляем
производную и подставляем в уравнение
неоднородной системы:
.Вычисляем
производную и подставляем в уравнение
неоднородной системы:![]()
![]() ,
,
![]()
![]() ,
Так как фундаментальная матрица
удовлетворяет уравнению однородной
системы, то
,
Так как фундаментальная матрица
удовлетворяет уравнению однородной
системы, то
![]() .
Поэтому в предыдущем уравнении (как и
всегда в методе вариации) сокращается
пара слагаемых. Получаем уравнение
.
Поэтому в предыдущем уравнении (как и
всегда в методе вариации) сокращается
пара слагаемых. Получаем уравнение
![]() .
Так как фундаментальная матрица не
вырождена (
.
Так как фундаментальная матрица не
вырождена (![]() ),
то отсюда получаем уравнение для
определения вектора
),
то отсюда получаем уравнение для
определения вектора
![]() :
:
![]() .Интегрируя,
получаем
.Интегрируя,
получаем![]() (здесь предполагается, что при вычислении
интеграла вектор констант не добавляется,
он уже добавлен в виде вектора
(здесь предполагается, что при вычислении
интеграла вектор констант не добавляется,
он уже добавлен в виде вектора
![]() ).Подставляя
в
).Подставляя
в
![]() ,
имеем
,
имеем
![]()
![]()
![]() (
(![]() )
)![]() .Здесь
в полном соответствии с теоремой о
структуре общего решения неоднородной
системы первое слагаемое представляет
собой общее решение однородной системы,
а второе слагаемое – частное решение
неоднородной системы.
.Здесь
в полном соответствии с теоремой о
структуре общего решения неоднородной
системы первое слагаемое представляет
собой общее решение однородной системы,
а второе слагаемое – частное решение
неоднородной системы.
Билет 13
1
