2.Первые интегралы нормальной системы дифференциальных уравнений, их применение и нахождение.

Задача Коши.

Найти решение системы , удовлетворяющее заданным начальным условиям .

Теорема Коши о существовании и единственности решения задачи Коши

Пусть функция непрерывна по совокупности переменных. Пусть существуют и непрерывны частные производные

Тогда существует и единственно решение задачи Коши.

Первые интегралы.

Пусть выполнены условия теоремы Коши. Рассмотрим решение задачи Коши при заданных начальных условиях . По теореме Коши оно существует и единственно. Это решение можно представить себе как некоторую интегральную кривую, соединяющие точки , .

Если в качестве начальных условий выбрать , то по теореме Коши через эту точку проходит та же единственная интегральная кривая, ее уравнение можно записать в виде . Зафиксируем , обозначим , получим соотношение – общий интеграл системы дифференциальных уравнений (векторное соотношение). Первый интеграл системы дифференциальных уравнений – скалярная составляющая общего интеграла. Общий интеграл системы дифференциальных уравнений – векторная функция, сохраняющая свое значение на решениях системы. Первый интеграл системы дифференциальных уравнений – скалярная функция, сохраняющая свое значение на решениях системы.

Знание одного первого интеграла позволяет понизить порядок системы на единицу. Знание общего интеграла дает общее решение системы, если только можно разрешить уравнение относительно .

Производной скалярной функции в силу системы называется

.

Скалярная функция является первым интегралом, если

.

Билет 7

1.Вывести формулу Ньютона-Лейбница для вычисления определённого интеграла.

Пусть функция непрерывна на отрезке - некоторая первообразная функции . Тогда .

Доказательство. Из теоремы о производной интеграла по переменному верхнему пределу следует, что , т.е. - первообразная для функции . По теоремам о первообразных две первообразных отличаются на константу т.е. Но по св-ву 4 опр. инт F. Тогда.Следовательно, .

2. Построение общего решения линейного однородного дифференциального уравнения 2-го порядка с постоянными коэффициентами в случае действительных различных корней характеристического уравнения.

Рассмотрим линейное однородное дифференциальное уравнение с постоянными коэффициентами второго порядка

.

Будем искать его решение в виде . Подставляя в дифференциальное уравнение, получим

Так как то имеем

- характеристическое уравнение. Решая его, получим корни

.

Возможно три случая:

1) действительны и различны,

2) - комплексно сопряженные корни,

3) - действительный кратный корень.

В случае действительных, различных корней получаем решения

.

Для того, чтобы доказать, что решения составляют фундаментальную систему решений и общее решение записывается в виде

,

надо проверить линейную независимость . Составим определитель Вронского

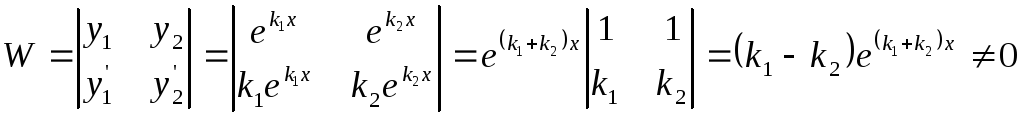, так как

.

Заметим, что для уравнения второго порядка проверять линейную независимость можно проще. Надо показать, что . Тогда столбцы определителя Вронского линейно независимы и . В нашем случае при .