-
Свойство аддитивности (по множеству)
-
(свойство
«ориентируемости» множества). -
-
. -
Если на отрезке
,
то
.
-
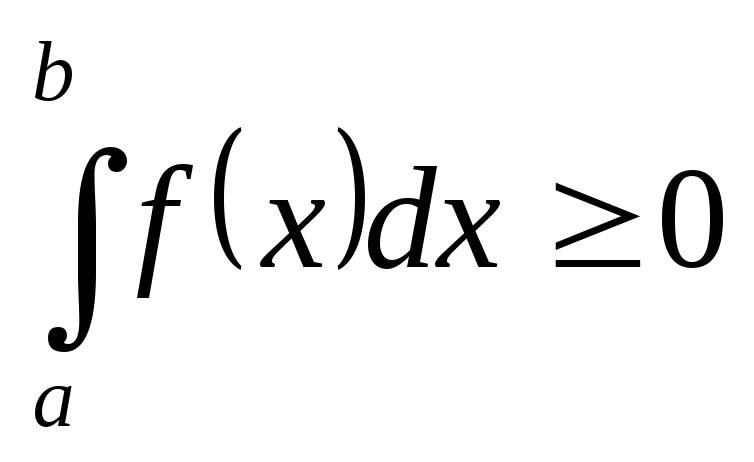Если на отрезке
,
то
. -
-
Определенный интеграл является функцией своих пределов, при фиксированных пределах интегрирования это – число. Он определен своими пределами. Поэтому он и называется определенным.
Доказательство:
-
Доказать теорему о структуре общего решения однородной системы линейных дифференциальных уравнений первого порядка.
Общее решение однородной системы представляет собой линейную комбинацию решений фундаментальной системы решений.
.
Доказательство.
Проверим, что
является общим решением, исходя из
определения общего решения.
-
- решение
однородной системы как линейная
комбинация ее решений (теорема о
свойствах решений). -
Зададим произвольные начальные условия
и покажем, что можно единственным
образом выбрать набор констант
,
при котором
.
Запишем это соотношение покоординатно
как систему уравнений относительно
.
Определитель этой
системы равен
,
так как решения линейно независимы.
Поэтому набор констант
определяется из системы уравнений
единственным образом. Теорема доказана.
Следствие. Общее решение однородной системы можно записать в виде
.
билет №4
-
Определение несобственного интеграла от непрерывной функции на бесконечном промежутке. Доказать признаки сравнения для таких интегралов.
Пусть отрезок
числовой оси неограничен. Это возможно
в трех случаях:
.
Определим несобственные интегралы как
пределы
,
,
.
В последнем интеграле a
и b
независимо друг от друга стремятся к
.
Если
,
то предел в правой части последнего
равенства называется главным значением
несобственного интеграла.
Если эти пределы существуют и конечны, то несобственные интегралы называются сходящимися. Если предел не существует или бесконечен, то такой несобственный интеграл называется расходящимся.
Если сходятся
интегралы от функций
,
то сходятся интегралы от функций
.
Это следует из теорем о пределах.
Рассмотрим интеграл
Дирихле
.
.
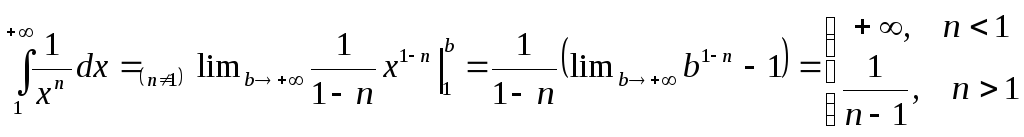При
,
интеграл расходится.
Итак, несобственный
интеграл Дирихле первого рода
сходится при
расходится при
Признаки сравнения несобственных интегралов (достаточные признаки сходимости и расходимости несобственных интегралов).
1 признак. Теорема.
Пусть при
выполнено неравенство
.
Если интеграл
сходится, то и интеграл
сходится.
Если интеграл
расходится, то и интеграл
расходится.
2 признак сравнения.
Теорема. Пусть
при x>a
.
Если существует конечный предел
,
то интегралы
,
,
сходятся или расходятся одновременно
(если один сходится, то и другой сходится,
если один расходится, то и другой
расходится).
Доказательство.
Из определения предела следует
.
Эталонами служат обычно интегралы Дирихле или интегралы от показательной функции.
-
Доказать теорему о структуре общего решения неоднородной системы линейных дифференциальных уравнений первого порядка.
Общее решение неоднородной системы равно сумме общего решения однородной системы и частного решения неоднородной системы.
Доказательство.
1)
- решение неоднородной системы по теореме
о свойствах решений.
2) Зададим произвольные
начальные условия
.
Выберем какое-либо частное решение
неоднородное системы
и
вычислим для него начальные условия в
.
Составим систему уравнений
и запишем ее покоординатно.
Определитель этой системы – вронскиан, он не равен нулю, так как составлен из лин независ решений, составляющих фср.. → набор констант из этой системы уравнений определяется однозначно. Теорема доказана.