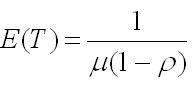8. Теоретические основы современных инфор-мационных сетей. Теория очередей.

Такие параметры, как число и длина пакетов, поступающих в сеть или проходящих через неё в любой момент времени, число вызовов, поступающих на вход сети за заданное время, продолжительность занятия (ресурса) - в общем случае подвержены статистическим изменениям. Поэтому для изучения их воздействия на сеть и получения соответствующих количественных характеристик должны применяться вероятностные методы. Ключевую роль в анализе сетей играет теория очередей (называемая также теорией массового обслуживания) Для сетей с коммутацией пакетов проблема очередей возникает совершенно естественно. Пакеты, поступающие на вход сети или промежуточного узла, на пути к пункту назначения накапливаются, обрабатываются с целью выбора подходящего канала передачи к следующему узлу, а затем считываются в этот канал, когда наступит время их передачи. Время, затраченное на ожидание передачи в накопителе, является важной мерой, характеризующей работу сети. Оно зависит от времени обработки в узле и длины пакета, а также от пропускной способности канала передачи и дисциплины обслуживания, применяемой при обработке пакета. Теория очередей возникает также при исследовании сетей с коммутацией каналов. Во-первых, при изучении обработки вызовов, во-вторых, при анализе зависимости между числом доступных каналов и вероятностью того, что вызов, требующий установление соединения, будет заблокирован или поставлен в очередь для ожидания обслуживания. 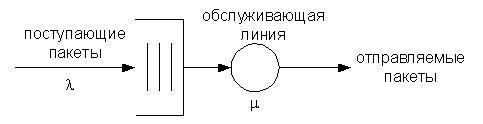Рассмотрим простейшую модель обслуживания: В качестве пакетов будем рассматривать пакеты данных для случая коммутации пакетов или вызовы для систем с коммутацией каналов. Пакты поступают случайным образом со скоростью λ в единицу времени. Они ожидают обслуживания в накопителе, и обслуживаются в соответствии с некоторой конкретной дисциплиной со средней скоростью μ пакетов в единицу времени. На рисунке показана одна обслуживающая линия ? это средство передачи (исходящий канал или линия, передающие пакеты или, в случае систем с коммутацией каналов, обрабатывающие вызовы), которое передает данные с предписанной скоростью С блоков данных в единицу времени. В более же общем случае могут быть доступны несколько обслуживающих линий, и в этом случае одновременно могут обслуживаться несколько пакетов. Длительность процесса обслуживания определяется длиной пакета или продолжительностью соединения. Если интенсивность поступления λ приближается к скорости обработки пакетов μ , очередь начинает расти. При накопителе конечной ёмкости очередь достигает наибольшей допустимой величины, а при переполнении накопителя поступление всех последующих пакетов будет заблокировано. Для однолинейных систем обслуживания стабильность обеспечивается при λ &60;μ . Введём параметр конецформыначалоформыρ = λ/μ . Его называют коэффициентом использования канала или интенсивностью нагрузки. Когда ρ приближается к 1 или превышает её, возникает область перегрузки, и поступающие пакеты блокируются более часто. Характеристики сети (время задержки, вероятность блокировки и т.д.) зависят также от вероятности состояний очереди. Для расчёта вероятностей состояния должны быть известны следующие характеристики: · процесс поступления пакетов (статистика входящих потоков); · распределение длин пакетов (распределение времени обслуживания); · дисциплина обслуживания (обслуживание в порядке поступления - ОПП или FIFO, некоторые дисциплины обслуживания с приоритетами). Для многолинейных систем вероятности состояний зависят также от числа обслуживающих линий. В теории массового обслуживания принято моделировать процесс поступления вызовов с помощью Пуассоновского процесса.

Пуассоновский процесс

Рассмотрим бесконечно малый промежуток времени Δ t (Δt → 0), проходящий между моментами t и t+Δt. При определении пуассоновского процесса используются три основные предпосылки: 1. вероятность одного поступления в течение времени Δt определяется в виде: λΔt+О(Δt), где О(Δt) - члены более высокого порядка, которыми мы можем пренебречь при Δt→0; 2. вероятность нулевого поступления в течение времени Δt равна 1-λΔt; 3. поступление - без последействия (без памяти), т.е. поступление в течение Δt не зависит от предыдущих поступлений. Если теперь рассмотреть большой промежуток времени Т, то вероятность p(k) того, что в промежутке Т произойдут k поступлений, равна: 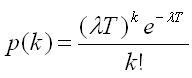, где k = 0, 1, 2, … Это равенство называется распределением Пуассона. Процесс обслуживания является полным аналогом процесса поступления и обладает всеми свойствами последнего. На основании этого вероятность завершения обслуживания в малом промежутке времени (t, t+Δt) в точности равна μ Δt + О(Δt), а вероятность незавершения обслуживания в промежутке (t, t+Δt) равна 1-μ Δt+О(Δt) независимо от предыдущих или последующих завершений. Ещё одно полезное свойство, объединяющее одну из причин, по которой Пуассоновский процесс часто используется для моделирования входящих потоков, заключается в том, что при объединении m независимых Пуассоновских потоков с произвольными интенсивностями λ₁, λ₂, … λ_m, объединённый поток также будет Пуассоновским с интенсивностью . 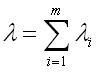В применении к сетям такое положение возникает, когда статистически объединяются пакеты иди вызовы от ряда источников, каждый из которых генерирует их с Пуассоновской интенсивностью.

Система обслуживания М/М/1

Система обслуживания М/М/1 - это система с одной обслуживающей линией, Пуассоновским входящим потоком, показательным распределением обслуживания и дисциплиной ОПП (обслуживание в порядке поступления). Диаграмма изменений состояний во времени для системы может быть изображена следующим образом: 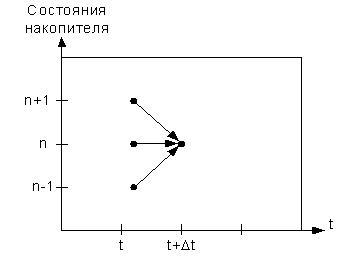Пусть процессы поступления и обслуживания определяются соответственно параметрами λ и μ . Определим вероятность p_n(t+Δt) того, что в момент времени t+Δt в системе будет находиться n клиентов (пакетов или вызовов). Из диаграммы видно, что в момент времени t система могла находиться только в состоянии n-1, n или n+1. Тогда мы можем записать: Вероятности перехода из одного состояния в другое получены в результате рассмотрения путей, по которым происходят эти переходы, и расчёта соответствующих вероятностей. Например, если система осталась в состоянии n, то могли произойти либо уход и одно поступление с вероятностью μ Δt, либо ни одного ухода или поступления с вероятностью , что и показано в первом случае. Производя упрощения, иcпользуя разложение в ряд Тейлора, можно показать что для стационарного состояния уравнение упрощается и принимает вид: (1) Форма уравнения (1) показывает, что при работе системы действует стационарный принцип равновесия: левая часть описывает интенсивность уходов из состояния n, а правая часть - интенсивность приходов в состояние n из n-1 или n+1. Чтобы существовали вероятности стационарного состояния, эти две интенсивности должны быть равны. Уравнение (1) может быть решено несколькими способами. При простейшем их них может быть использовано условие равновесия потоков. 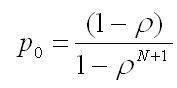В результате можно получить решение для установившегося режима: (2) Если рассмотреть случай конечной очереди, вмещающей не более N пакетов, то можно показать, что в этом случае: 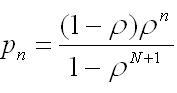В частности, вероятность того, что очередь заполнена, совпадает с вероятностью блокировки: 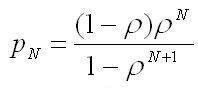На следующем рисунке приведён график вероятности блокировки в зависимости от нормированной нагрузки ρ. 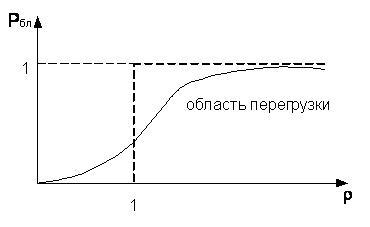Область ρ>1 называется областью перегрузки или скученности. Производительность системы, которая близка к нагрузке λ при малых ρ, выравнивается и при возрастании ρ приближается к пропускной способности μ . Рассмотрим область ρ<1. 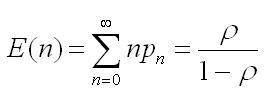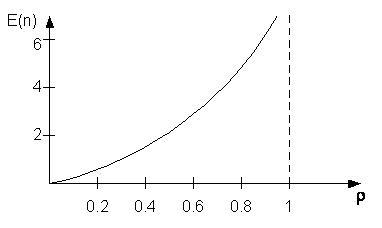На основании определения среднего значения p_n, проведя суммирование, получим среднее число E(n) клиентов в системе, включая находящихся на обслуживании: Это отражено на следующем рисунке: При увеличении ρ среднее число клиентов в очереди резко возрастает за счёт (1-ρ) в знаменателе. Можно заметить, что при росте нагрузки системы растёт её производительность, однако при этом блокируется всё большее количество клиентов, а следовательно, растёт E(n), что ведёт к увеличению времени задержки в очереди. Для нахождения времени задержки используют формулу Литтла: λE(T) = E(n), где E(T) - среднее время задержки в системе. Для системы М/М/1, используя предыдущие формулы, можно получить: